Weyl electrons kiss
Topology, the mathematical description of the robustness of form, appears throughout physics, and provides strong constraints on many physical systems. It has long been known that it plays a key role in understanding the exotic phenomena of the quantum Hall effect. Recently, it has been found to generate robust and interesting bulk and surface phenomena in “ordinary” band insulators described by the old Bloch theory of solids. Such “topological insulators,” insulating in the bulk and metallic on the surface, occur in the presence of strong spin-orbit coupling in certain crystals, with unbroken time-reversal symmetry [1].
It is usually believed that such topological physics is obliterated in materials where magnetic ordering breaks time-reversal symmetry. This is by far the most common fate for transition-metal compounds that manage to be insulators—so called “Mott insulators,” which owe their lack of conduction to the strong Coulomb repulsion between electrons. In an article appearing in Physical Review B, Xiangang Wan from Nanjing University, China, and collaborators from the University of California and the Lawrence Berkeley National Laboratory, US, show that this is not necessarily the case, and describe a remarkable electronic structure with topological aspects that is unique to such (antiferro-)magnetic materials [2]. The state they describe is remarkable in possessing interesting low-energy electron states in the bulk and at the surface, linked by topology. In contrast, topological insulators, like quantum Hall states, possess low-energy electronic states only at the surface.
The theory of Wan et al., which uses the LDA+U numerical method, is a type of mean field theory. As such, the low-energy quasiparticle excitations are described simply by noninteracting electrons in a background electrostatic potential and, in the case of a magnetically ordered phase, by a spatially periodic exchange field. It is possible to follow the evolution of the electronic states as a function of the U parameter, which is used to model the strength of Coulomb correlations. They apply the technique to iridium pyrochlores, , where is a rare earth element. These materials are known to exhibit metal-insulator transitions (see, e.g., Ref. [3]), indicating substantial correlations, and are characterized by strong spin-orbit coupling due to the heavy element (iridium). In the intermediate range of U, which they suggest is relevant for these compounds, Wan et al. find an antiferromagnetic ground state with the band structure of a “zero-gap semimetal,” in which the conduction and valence bands “kiss” at a discrete number ( !) of momenta. The dispersion of the bands approaching each touching point is linear, reminiscent of massless Dirac fermions such as those observed in graphene.
This would be interesting in itself, but there are important differences from graphene. Because of the antiferromagnetism, time-reversal symmetry is broken, and as a consequence, despite the centrosymmetric nature of the crystals in question, the bands are nondegenerate. Thus two—and only two—states are degenerate at each touching point, unlike in graphene where there are four. In fact, the kissing bands found by Wan et al. are an example of accidental degeneracy in quantum mechanics, a subject discussed in the early days of quantum theory by von Neumann and Wigner (1929), and applied to band theory by Herring (1937). The phenomenon of level repulsion in quantum mechanics tends to prevent such band crossings. To force two levels to be degenerate, one must consider the Hamiltonian matrix projected into this subspace: not only must the two diagonal elements be made equal, the two off-diagonal elements must be made to vanish. This requires three real parameters to be tuned to achieve degeneracy. Thus, without additional symmetry constraints, such accidental degeneracies are vanishingly improbable in one and two dimensions, but can occur as isolated points in momentum space in three dimensions (the three components of the momentum serving as tuning parameters). An accidental touching of this type is called a diabolical point. The matrix Schrödinger equation in the vicinity of this point is mathematically similar to a two-component Dirac-like one, known as the Weyl equation. Thus the low-energy electrons in this state behave like Weyl fermions. A property of such a diabolical point is that it cannot be removed by any small perturbation, but may only disappear by annihilation with another diabolical point.
Actually such diabolical points were suggested previously in a very similar context by Murakami [4], who argued that such a semimetallic state would naturally arise as an intermediate between a topological insulator and a normal band insulator. That theory does not directly apply here, since Murukami assumed time-reversal symmetry, which is broken in Wan et al.’s calculations. However, inversion symmetry plays a similar role, and indeed the latter authors find that the Weyl semimetal is intermediate between an “ordinary” Mott insulator and an “axion insulator,” somewhat analogous to the topological insulator. The axion insulator has a quantized magnetoelectric response identical to that of a (strong) topological insulator, but lacks the protected surface states of the topological insulator.
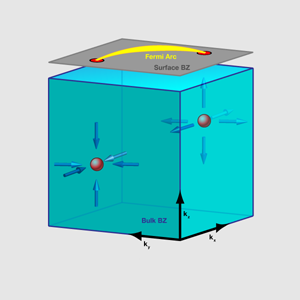
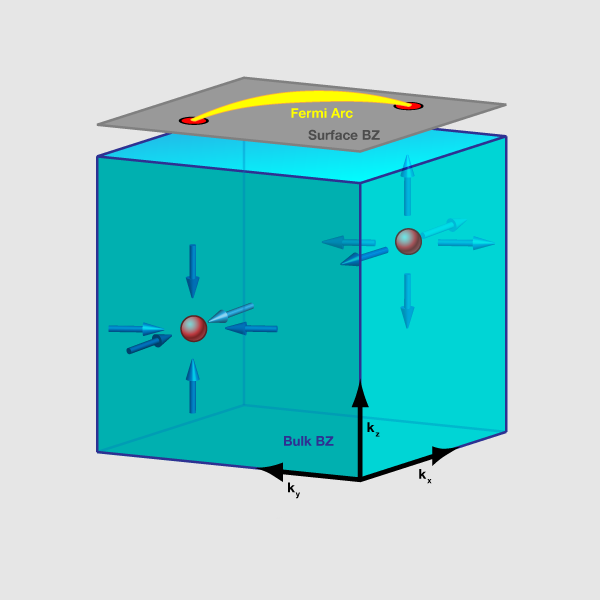
What is really new and striking about the recent paper is the implications for surface states. Remarkably, they find that certain surfaces (e.g., and faces) have bound states at the Fermi energy, and that these states do not form the usual closed Fermi surfaces found in or metals. Instead, the states at the Fermi energy form open “arcs,” terminating at the projection of diabolical points onto the surface Brillouin zone (see Fig. 1). Fermi arcs have appeared before in physics in experimental studies of high-temperature cuprate superconductors. However, in that context they are mysterious and puzzling, because they would seem to be prohibited by topology. The Fermi surface is by definition the boundary between occupied and unoccupied states, and if it terminates then one could go “around” the termination point and smoothly change from one to another, which is impossible at zero temperature. At a surface, this paradox is avoided because the surface states may unbind into the bulk when going around the end of a Fermi arc.
This theoretical proposal provides plenty of motivation for future experiments. Observation of the Fermi arcs would be striking, and provide a useful metric to gauge the empirical ones seen in the cuprates. The bulk Weyl fermions are also interesting and would be exciting to try to observe in transport. Simple phase-space considerations suggest that the low-energy electrons should be remarkably resistant to scattering by impurities. Most of this theory could apply to many other materials—the only necessary conditions are significant spin-orbit coupling and antiferromagnetic order preserving inversion symmetry (and the latter is only essential for some of the physics). More generally, the work widens the range of unusual states of matter that have been proposed to arise in the regime of strong spin-orbit coupling and intermediate correlation. Despite the uncommon aspects described above, Wan et al.’s work is a mean-field theory, and yet more exotic possibilities have been suggested that are not describable in this way (e.g., Ref. [5]). Hopefully this is just the beginning of the theoretical and experimental exploration of this fascinating regime.
References
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010)
- X. Wan, A. M. Turner, A. Vishwanath, and S. Y. Savrasov, Phys. Rev. B 83, 205101 (2011)
- K. Matsuhira and et al, J. Phys. Soc. Jpn. 76, 043706 (2007)
- S. Murakami, New J. Phys. 9,356 (2007)
- D. A. Pesin and L. Balents, Nature Phys. 6, 376 (2010)