The antineutrino vanishes differently
CPT symmetry, the combination of charge conjugation, parity inversion, and time reversal, is a fundamental symmetry of particle and nuclear physics and is considered sacred. It is conserved in field theories that explain the strong, weak, and electromagnetic interactions. In the lepton sector, CPT symmetry requires that muon neutrino disappearance oscillations be identical to muon antineutrino disappearance oscillations in vacuum. A test of CPT symmetry was recently performed by the MINOS experiment at Fermilab, which, due to its magnetic field, is the first experiment to distinguish μ- and μ+ tracks and separately measure the disappearance of muon neutrinos and muon antineutrinos [1]. (Previous experiments have measured a mixture of neutrino and antineutrino oscillations.) Remarkably, as reported in Physical Review Letters, MINOS appears to observe a difference between muon neutrino and muon antineutrino disappearance [1].
The “atmospheric neutrino problem,” a deficit of atmospheric muon neutrinos relative to electron neutrinos, was initially observed by the IMB and Kamioka experiments and was then shown to be due to νμ→ντ oscillations by the SuperKamiokande experiment in 1998. Neutrino oscillations occur if there is mixing between neutrino flavors and if individual neutrino flavors consist of a linear combination of different neutrino mass eigenstates. In the case of two-flavor mixing, e.g., mixing between νμ and ντ, then the probability that a νμ will oscillate into a ντ is given by
where θ is the mixing angle, Δm2 is the difference in squared masses of the two mass eigenstates in eV2, L is the distance travelled by the neutrino in km, and E is the neutrino energy in GeV.
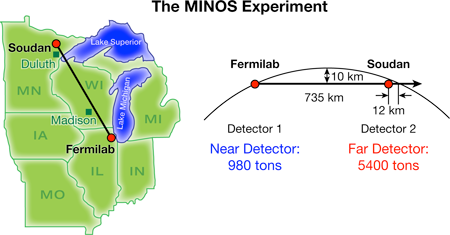
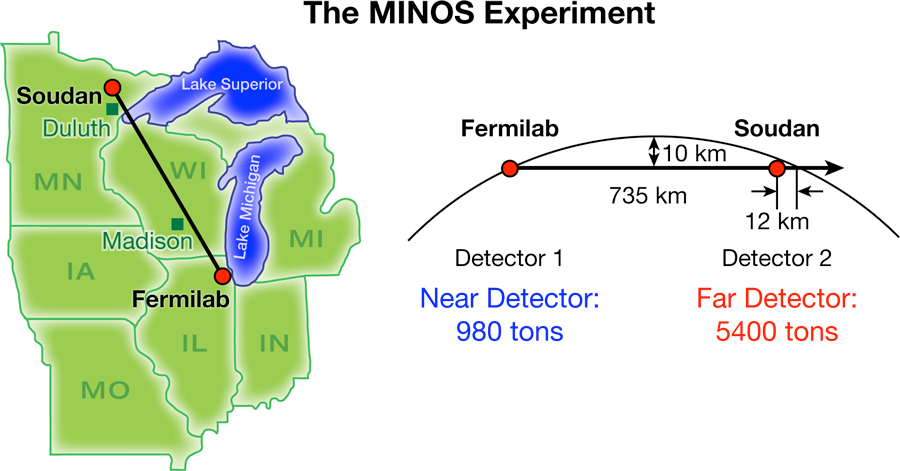
In addition to the IMB, Kamioka, and SuperKamiokande atmospheric neutrino experiments, the K2K, MINOS, and OPERA accelerator neutrino experiments have confirmed the νμ→ντ oscillation resolution of the “atmospheric neutrino problem.” The most precise measurement of νμ→ντ oscillations comes from the MINOS experiment, which consists of two similar detectors [2] located at distances of 1.04km [Near Detector (ND)] and 735km [Far Detector (FD)] from the particle production target. Neutrinos are produced by 120- GeV protons from the Fermilab Main Injector interacting on a graphite target, followed by magnetic horns that focus either positive pions and kaons to produce a dominantly νμ beam, or negative pions and kaons to produce an enhanced ˉνμ beam. The ND, located at Fermilab, and the FD, located in the SOUDAN Underground Laboratory in northern Minnesota (see Fig. 1), are tracking calorimeters consisting of planes of magnetized steel ( ∼1.4T) interspersed with planes of plastic scintillator. Neutrino interactions in the steel produce muons whose energy is measured by either the range of the contained muon track or by the curvature of the muon track in the magnetic field. This curvature also determines the charge of the muon and whether the incident neutrino is a νμ or ˉνμ. The hadronic energy is determined from the total amount of light produced in the scintillator. The total neutrino energy is the sum of the muon energy and the associated hadronic energy. MINOS is designed to make a precision measurement of νμ and ˉνμ disappearance by comparing the neutrino energy distribution in the FD (after neutrinos have oscillated) to the neutrino energy distribution in ND (before neutrinos have oscillated).
MINOS has made the world’s best measurement of νμ disappearance oscillations [3]. Using a data sample corresponding to 7.25×1020 protons on target (POT), MINOS measures the best-fit νμ oscillation parameters to be Δm2=2.32×10-3eV2 and sin22θ=1.0. Antineutrino experiments are difficult, due to their low event rate compared to neutrino experiments. Nevertheless, based on 1.71×1020 POT, MINOS has also reported the first direct observation of ˉνμ disappearance oscillations [1] and measures the ˉνμ oscillation parameters to be Δm2=[3.36+0.46-0.40(stat.)±0.06(syst.)] ×10-3eV2 and sin22θ=0.86+0.11-0.12(stat.)±0.01(syst.). The no-oscillation hypothesis in antineutrino mode is disfavored at 6.3 standard deviations; however, it is significant that the νμ and ˉνμ disappearance parameters appear to be different. As stated in the paper, “The probability that the underlying νμ and ˉνμ parameters are identical is 2.0%.”
What could explain this apparent difference between muon neutrino and muon antineutrino disappearance? First, it is possible that the difference is just due to a statistical fluctuation. This possibility will be tested by additional MINOS data to be taken over the next few years. If the difference is not a statistical fluctuation, then it is possible that it is due to nuclear effects [4], which can cause a difference in the energy reconstruction of neutrino events compared to antineutrino events. A large energy difference is unlikely but could arise if the hadronic energy is misreconstructed. Neutrino events have a higher fraction of hadronic energy than antineutrino events, and as the neutrino energy is needed for the determination of Δm2, a mismeasurement of the neutrino energy then results in an incorrect measurement of Δm2.
If the apparent difference between muon neutrino and muon antineutrino disappearance is not due to a statistical fluctuation or to nuclear effects, then we would have to consider new physics beyond the standard model. Indeed, global fits to the world neutrino and antineutrino oscillation data [5] encounter tension between the neutrino and antineutrino data sets and favor different neutrino and antineutrino oscillation parameters. One possible beyond the standard model solution involves nonstandard interactions [6], which would affect neutrinos and antineutrinos passing through matter (as is the case for MINOS) differently. A more extreme possibility is that Lorentz symmetry is violated [7] or CPT symmetry is violated [8], and that neutrino oscillation parameters are different from antineutrino parameters. If this were the case, then the impact on nuclear and particle physics would be profound.
Fortunately, there are several experiments that are either taking data or being constructed that will be able to test this possible difference between muon neutrino and muon antineutrino disappearance. The SciBooNE and MiniBooNE experiments at Fermilab, located at distances of 0.10km and 0.54km from the neutrino source, took data at the same time in both neutrino mode and antineutrino mode and are performing a joint analysis of their disappearance data. Also, the T2K experiment in Japan has detectors at distances of 0.28km and 295km, and is now taking data with neutrinos. T2K has the capability of switching to antineutrinos in a few years. In addition, the NO νA experiment at Fermilab is under construction and should begin taking data in a couple of years with detectors at distances of 1.0km and 810km. Finally, the IceCube experiment at the South Pole is measuring high-energy atmospheric neutrinos and antineutrinos and will be sensitive to disappearance over distances of approximately 100 to 10,000km. Will neutrino experiments continue to surprise us? Is CPT symmetry conserved in the lepton sector? Stay tuned.
References
- P. Adamson et al. (MINOS Collaboration), Phys. Rev. Lett. 107, 021801 (2011)
- D. G. Michael et al., Nucl. Instrum. Meth. A 596, 190 (2008)
- P. Adamson et al., arXiv:1103.0340
- G. T. Garvey (private communication)
- G. Karagiorgi et al., Phys. Rev. D 80, 073001 (2009); Carlo Giunti and Marco Laveder, 83, 053006 (2011); 82,093016 (2010); 82,113009 (2010); Joachim Kopp, Michele Maltoni, and Thomas Schwetz, arXiv:1103.4570
- A. Friedland, C. Lunardini, and M. Maltoni, Phys. Rev. D 70, 111301 (2004); W. A. Mann et al., 82, 113010 (2010); J. Kopp et al., 82, 113002 (2010); Netta Engelhardt, Ann E. Nelson, and Jonathan R. Walsh, arXiv:1002.4452
- Jorge S. Diaz and V. Alan Kostelecky, arXiv:1012.5985
- Gabriela Barenboim and Joseph D. Lykken, arXiv:0908.2993