When Two Baryons Scatter
In physics, much can be learned from simple models that are elementary enough to be solved analytically. An example is the Gross-Neveu model, which describes massless fermions, interacting exclusively through a four-fermion contact term, in one dimension.
The “baryons” in this model are a series of multifermion bound states. In the limit that the number of fermions is large, the model is exactly soluble, making it for field theory what the solution of the hydrogen atom problem is in quantum mechanics. The model is solved by integrating out the fermions to obtain an effective theory of bosons, which are analogous to the sigma and pion fields that mediate the interactions between nucleons. For static processes, the theory is well understood.
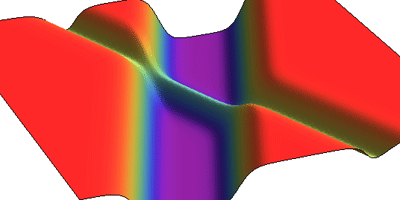
Now, in a paper appearing in Physical Review D, Gerald Dunne at the University of Connecticut in Storrs and colleagues go beyond the purely static case to treat the time-dependent problem of two baryons scattering from one another. They do this by explicitly solving the time-dependent Hartree-Fock equations in the effective bosonic theory. As one example, they calculate the behavior of the effective sigma field in the model, when one baryon is very small, and one is very large, and they scatter at equal and opposite relativistic velocities.
Dunne et al.’s solution realizes a long sought dream of nuclear physics, namely, that nucleons can be constructed as the solitons of an effective bosonic model. Along different lines, in conducting polymers like polyacetylene, the electron-phonon interaction gives rise to solitonic excitations called polarons, which (mathematically) have a one-to-one correspondence with baryons in the Gross-Neveu model. Dunne et al.’s model could therefore be used to study polaron dynamics and to make experimentally testable predictions. – Robert D. Pisarski