Homing in on the Higgs Boson

Howard E. Haber

Viewpoint

Homing in on the Higgs Boson

Howard E. Haber

Department of Physics,University of California, Santa Cruz, 1156 High Street, Santa Cruz, CA 95064, USA

March 13, 2012• Physics 5, 32

There are encouraging hints that the Higgs boson may have been observed at the Large Hadron Collider.

Figure caption — **Figure 1:** Where to hunt for the Higgs? The standard model predicts the probability (or “branching ratio” denoted BR) that a Higgs boson will decay into a particular set of final state particles. As an example, the probability that the Higgs boson will decay into two photons (magenta line) is much lower than the probability it will decay into a bottom and anti-bottom quark (black line), but the background for the two-photon final state is significantly less severe than for the bottom quark final state, so this is a better place to search for the Higgs boson. The branching ratios into other final states employed in the LHC Higgs searches are also shown; the thickness of the lines denote the theoretical uncertainty.

The mediators of the weak force—the $W$ and $Z$ bosons—are both roughly $100$ times more massive than the proton, while the photon, which mediates the electromagnetic force, is massless. Based on symmetry principles, one would have expected the $W$ , $Z$ , and photon (collectively called gauge bosons) to all be massless. In order to generate the required symmetry breaking, one must invent a particular set of new particles and interactions, which ultimately provide an explanation of the origin of mass of the elementary particles. The simplest way to do this, and the one that is incorporated in the standard model of particle physics, predicts the existence of a particle called the Higgs boson [1]. The interactions of the Higgs boson with the quarks, leptons, and gauge bosons of the standard model are uniquely predicted by the theory, but the mass of the Higgs boson is a free parameter that can only be determined by experiment [2].

One of the most important missions of the Large Hadron Collider (LHC) is to ascertain the origin of mass by discovering the Higgs boson as envisioned by the standard model (or, if no Higgs is found, perhaps by discovering alternative phenomena that can be attributed to the symmetry-breaking mechanism). Three papers now appearing in Physical Review Letters, two from the ATLAS Collaboration [3,4] and one from the CMS Collaboration [5], report searches for the Higgs boson in the debris of high-energy proton-proton collisions at the LHC. The results of these searches, and several others being published elsewhere [6], were announced in December, 2011. Collectively, they have shown that the Higgs boson of the standard model, if it exists, must lie in a narrow range of masses around $126$ giga-electron-volts ( $GeV$ ). Moreover, an excess of events around this mass value provides a tantalizing hint that experimentalists could be on the verge of discovering the long-sought particle.

Although the LHC has taken over the search for the Higgs boson, it does so with the knowledge, accumulated from previous experiments, that already tells us where the Higgs mass is likely—and unlikely—to be. From experiments at the CERN LEP collider [7], which shut down in 2000, it is known that the standard model Higgs boson mass cannot be below $114 GeV$ , while subsequent data from the Fermilab Tevatron [8], which shut down in 2011, excludes a Higgs boson mass between $156$ and $177 GeV$ . (As is common in particle physics, mass is reported in terms of its energy equivalent.) Even without a direct discovery, the data from the LEP and Tevatron colliders have been able to place additional constraints on the allowed values of the Higgs mass. Results from measurements performed at the LEP and Tevatron colliders can be compared with theoretical predictions. Based on a statistical analysis of these data in the framework of the standard model (which depends indirectly on the unknown Higgs mass) the Higgs mass cannot be larger than $169 GeV$ [9]. Combining the direct Higgs search limits quoted above with the indirect constraints implies that the standard model is viable if, and only if, the standard model Higgs boson mass lies between $114$ and $156 GeV$ [10].

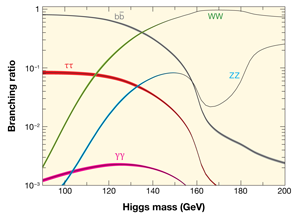
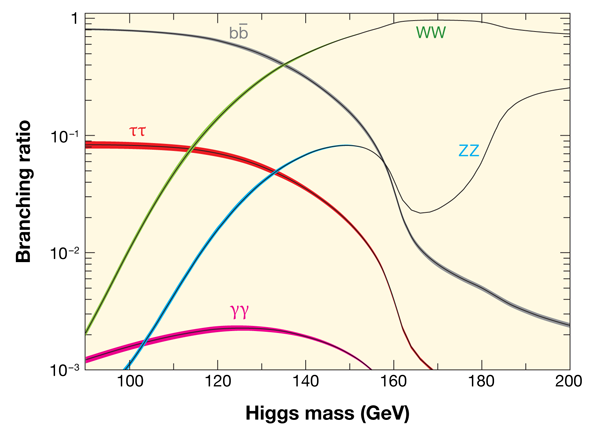
If a Higgs boson is produced in a high-energy collision, it should, according to theory, be extremely unstable and immediately decay into lighter elementary particles. The standard model predicts the relative probabilities of a Higgs boson decaying into a particular set of final state particles, as shown in Fig. 1, and it is an excess of these particles relative to background events—the numerous other processes that can yield the same final state particles without there ever having been a Higgs boson—that particle physicists aim to measure.

In 2011, the LHC collided two proton beams at $7$ tera-electron-volts ( $TeV$ ). On average, more than $100$ million collisions per second took place, but most of these collisions were “conventional,” in that they involved only the most common elementary particles. If the standard model is correct, then on rare occasions, a Higgs boson should have been produced. Assuming the Higgs mass lies in the expected mass range, about $75, 000$ Higgs bosons were produced in the ATLAS and CMS collider detectors in 2011.

As shown in Fig. 1, for Higgs masses below $135 GeV$ , most of these Higgs bosons should decay into a pair of bottom quarks. However, because there are so many bottom quarks produced each second at the LHC, the bottom quark background would overwhelm the tiny signal associated with a Higgs boson. Instead, the rare event in which the Higgs bosons decay into two photons, with a probability of roughly one in five-hundred (the magenta line in Fig. 1), is actually a better place to look for the Higgs boson. In the 2011 LHC data, fewer than $150$ Higgs bosons should have decayed into photon pairs, but although there is a background of two-photon events, it is statistically manageable. What ATLAS has found [4] is a potentially significant number of two-photon events, whose invariant mass clusters around $126 GeV$ , above the expected background. (Although each photon is massless, the two-photon pair can collectively be assigned a mass value, called the invariant mass, that depends on the kinematical properties of the pair.) If the two photons originated from a decaying Higgs boson, their invariant mass can be identified with the mass of the decaying Higgs boson; that is, a Higgs mass of $126 GeV$ .

Another rare but striking Higgs decay (corresponding to the light blue curve in Fig. 1 labeled $Z Z$ ) is one that results in a $Z$ boson and a pair of electrons or muons, collectively called leptons. Subsequently, the $Z$ boson can also decay into a pair of leptons, in which case the end result of the Higgs decay is an event with four leptons. Once again, there is a background from more conventional processes, but this background is also manageable. In their search for four-lepton final states, CMS was able to exclude the existence of a Higgs boson over a significant range of masses [5]. Indeed, within the preferred Higgs mass range of the standard model, CMS rules out Higgs boson masses above $134 GeV$ . However, CMS also identified excesses in four-lepton events in regions of the four-lepton invariant mass around $119 GeV$ , $126 GeV$ , and $320 GeV$ . Although none of the three observations is statistically significant in itself, other experimental measurements provide some guidance: The excess at $320 GeV$ is probably an ordinary statistical fluctuation, while the excess at $126 GeV$ is more striking in light of the ATLAS two-photon data [4]. Indeed, a Higgs boson of $126 GeV$ would be expected to produce a few four-lepton events above the predicted background, which is what CMS observed [5]. The excess at $119 GeV$ is, however, difficult to interpret with the present data set.

So, where do we stand at this moment in time? Whether or not the various excesses above background described above turn out to be statistical fluctuations, the ATLAS and CMS collaborations have already significantly narrowed the allowed mass range for the standard model Higgs boson. These results, together with the ATLAS and CMS searches [3,6] for Higgs bosons decaying into other final states (e.g., in [3] ATLAS examined the decay into a pair of $W$ bosons), and the indirect Higgs mass constraints from previous experiments, imply that the Higgs boson of the standard model (if it exists) must have a mass that lies between $115.5 GeV$ and $127 GeV$ [12]. Moreover, it is tempting to attribute the small excess of events with invariant mass of $126 GeV$ to a possible Higgs boson of the same mass.

Nevertheless, this intriguing hint is not (yet) a Higgs boson observation, and it is certainly not a Higgs boson discovery. The statistical evidence for the Higgs boson is not sufficiently compelling, though the LHC data that will be collected in 2012 could be decisive since the collider will be ramped up to $8 TeV$ and the data samples are expected to be $3$ times larger than those collected in 2011. An extrapolation to the anticipated 2012 data set suggests that if the standard model Higgs boson exists in the expected mass range, then a statistically significant signal (of $5$ standard deviations or greater) will emerge. If this happens, can we claim the discovery of the Higgs boson? Strictly speaking, the answer is no. If the signal matches (within the statistical uncertainty) the one expected, then all one can say is that the signal is consistent with that of the standard model Higgs boson, but additional data will be required to confirm in detail that the properties of the newly discovered particle match the theoretically expected properties of the standard model Higgs boson. If the signal deviates significantly from the one expected, or if the statistical significance of the signal is greatly reduced after analyzing the 2012 LHC data, then it will be possible to exclude the existence of the standard model Higgs boson over its entire allowed mass range, in which case the simplest symmetry-breaking mechanism employed by the standard model will have to be replaced by more complicated symmetry-breaking dynamics. Whichever path nature chooses, 2012 is sure to be a watershed year in particle physics.

References

For a fascinating exposition of the history of the Higgs boson, see Frank Close, The Infinity Puzzle (Oxford University Press, Oxford, 2011)[Amazon][WorldCat]
For reviews of Higgs boson theory and phenomenology, see e.g., M. Carena, and H.E. Haber, Prog. Part. Nucl. Phys. 50, 63 (2003); A. Djouadi, Phys. Rept. 457, 1 (2008)
G. Aad et al. (ATLAS Collaboration), Phys. Rev. Lett. 108, 111802 (2012)
G. Aad et al. (ATLAS Collaboration), Phys. Rev. Lett. 108, 111803 (2012)
S. Chatrchyan et al. (CMS Collaboration), Phys. Rev. Lett. 108, 111804 (2012)
G. Aad et al. (ATLAS Collaboration), Phys. Lett. B (2012), DOI: 10.1016/j.physletb.2012.02.044 (to be published); S. Chatrchyan et al. (CMS Collaboration), Phys. Lett. B (2012), DOI: 10.1016/j.physletb.2012.02.064 (to be published)
ALEPH Collaboration, DELPHI Collaboration, L3 Collaboration, OPAL Collaboration, and The LEP Working Group for Higgs Boson Searches, Phys. Lett. B 565, 61 (2003)
TEVNPH (Tevatron New Phenomena and Higgs Working Group) and CDF and D0 Collaborations, arXiv:1107.5518 (hep-ex)
M. Baak, M. Goebel, J. Haller, A. Hoecker, D. Ludwig, K. Moenig, M. Schott, and J. Stelzer, arXiv:1107.0975 (hep-ph)
Based on the most recent data reported (http://tevnphwg.fnal.gov/results/SM_Higgs_Winter_12/) by the Tevatron experimental collaborations on 7 March, 2012 (without the constraints from the 2011 LHC data), the upper bound of the standard model Higgs mass is lowered to 147 GeV
A. Denner, S. Heinemeyer, I. Puljak, D. Rebuzzi, and M. Spira, Eur. Phys. J. C 71, 1753 (2011)
The most recent combined ATLAS analysis of the 2011 data reported on March 7, 2012 (https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2012-019/) excludes standard model Higgs masses below 122.5 GeV (although ATLAS cannot quite exclude masses between 117.5 GeV and 118.5 GeV). Thus, the only standard model Higgs masses that are not excluded are most likely to lie between 122.5 and 127 GeV

About the Author

Howard Haber is a Distinguished Professor of Physics at the University of California, Santa Cruz. He is one of four authors of the book, The Higgs Hunter’s Guide, first published in 1990. In 2017, he was a co-recipient of the J. J. Sakurai Prize for Theoretical Particle Physics, in recognition of his instrumental contributions to the theory of the properties, reactions, and signatures of the Higgs boson. Haber’s research explores new theoretical directions beyond the standard model of particle physics, with an emphasis on using current and future high-energy colliders to search for Higgs bosons in models of extended Higgs sectors and for evidence of supersymmetric phenomena.