Mirror, Mirror

Jennifer A. Dionne

Viewpoint

Mirror, Mirror

Stanford University, Department of Materials Science and Engineering, Durand Building, 496 Lomita Mall, Stanford, CA 94305, USA

March 26, 2012• Physics 5, 38

Collective electron excitations in metals, called plasmons, can play an important role in second-harmonic generation of light.

Figure caption — **Figure 1:** Second-harmonic generation—the conversion of low-energy photons to higher-energy photons—is enhanced near a thin metallic film by surface plasmons. To excite plasmons, light is directed through a prism onto a metal nanofilm. Individual photons each excite surface plasmons, which can then combine to form a higher energy plasmon and photon. Here, plasmons are represented by curves indicating the intensity profile of their electric field, which decays exponentially away from the metal surface.

In the fairy tale Snow White, an evil queen possesses a magical mirror that can provide answers to any question. Real mirrors may not be as animated, but scientists have observed many unusual phenomena by studying the way light interacts with metallic films. For example, nanostructured metal films can localize optical fields, confining light to dimensions much smaller than the wavelength. Further, nanostructured metals can serve as optical antennas, funneling photons to specific spatial regions and enhancing local electromagnetic fields. These two unique optical properties of metallic films—localization and enhancement of optical fields—emerge from surface plasmon resonances. As collective oscillations of conduction electrons in the metal, surface plasmons have enabled numerous technological advances, such as single-molecule Raman spectroscopy [1] and enhanced solar absorption in photovoltaics and photocatalysis [2].

Despite these advances, many questions remain regarding the role of surface plasmons in enhancing optical processes, especially nonlinear processes involving two or more interacting photons. On the one hand, surface plasmons could just be “catalysts” of nonlinear optical processes, increasing the rate at which photons interact with each other. On the other hand, plasmons could also directly participate in nonlinear optical process, combining with photons or other plasmons to increase the optical output. Unraveling the mechanism of plasmon-enhanced nonlinearities has been a long-standing challenge, but in a paper appearing in Physical Review Letters, Nicolai Grosse and colleagues at the Berlin Institute of Technology, Germany, present the results of experiments that elegantly identify the role of plasmons in nonlinear optical phenomena [3]. In particular, they show that surface plasmons do not simply modify photon interactions, but rather directly combine and annihilate with other plasmons, which convert into outgoing photons.

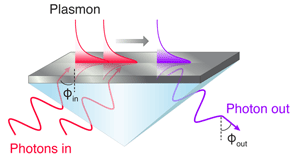
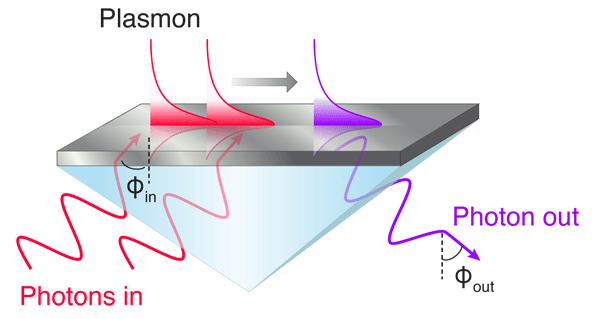
As a model nonlinear system, Grosse and colleagues consider plasmon-enhanced second-harmonic generation (SHG). Historically, observations of surface-plasmon-enhanced SHG date back to 1974 in a seminal set of experiments by Simon [4]. In these early experiments, low-energy photons illuminated a semitransparent silver film through a glass prism (see Fig. 1). Upon reflection, photons with twice the energy of the incident photons were observed. The intensity of such second-harmonic light was recorded for a range of incident excitation angles. Because of the silver-on-prism configuration (called a Kretschmann geometry), surface plasmons could only be excited over a narrow range of incident angles, allowing observation of SHG both with and without plasmons. Simon’s results indicated that SHG could be enhanced by over one and a half orders of magnitude in the presence of surface plasmons. More recent results indicate that plasmon-assisted nonlinear processes can be enhanced by factors up to $2000$ [5].

Such giant enhancements of nonlinear processes promise a number of exciting applications. For example, a highly efficient “up-converting” material that converts two lower-energy photons into a higher-energy photon could greatly increase the efficiency of solar cells, from $30 %$ to over $44 %$ [6,7]. Further, plasmon-enhanced SHG could advance the development of nanoscale coherent light sources for lasing, microscopy, and spectroscopy [8]. However, to capitalize on the promises afforded by plasmon-enhanced nonlinearities, it is crucial to identify the precise plasmon and photon interactions occurring in these processes.

Grosse and colleagues tackle the problem by revisiting the Kretschmann configuration of Simon’s experiment. Because nonlinear interactions conserve momentum, they can be uniquely identified in momentum space. Among the possible nonlinear interactions in SHG are all of the momentum-conserving combinations of low-energy photons ( $f$ ) and plasmons ( $p$ ) that yield a higher-energy photon or plasmon. For example, two low-energy photons can directly combine to form a higher-energy photon: $f (ω) + f (ω) \to f (2 ω)$ , where $ω$ is the photon frequency (energy divided by Planck’s constant). Alternatively, a photon and a plasmon could combine to form a higher-energy photon: $f (ω) + p (ω) \to f (2 ω)$ , or two plasmons could combine and annihilate to create a higher-energy photon, $p (ω) + p (ω) \to f (2 ω)$ . A number of additional momentum-conserving photon and plasmon combinations are also allowed.

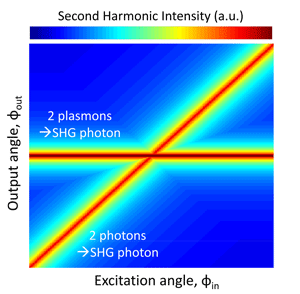
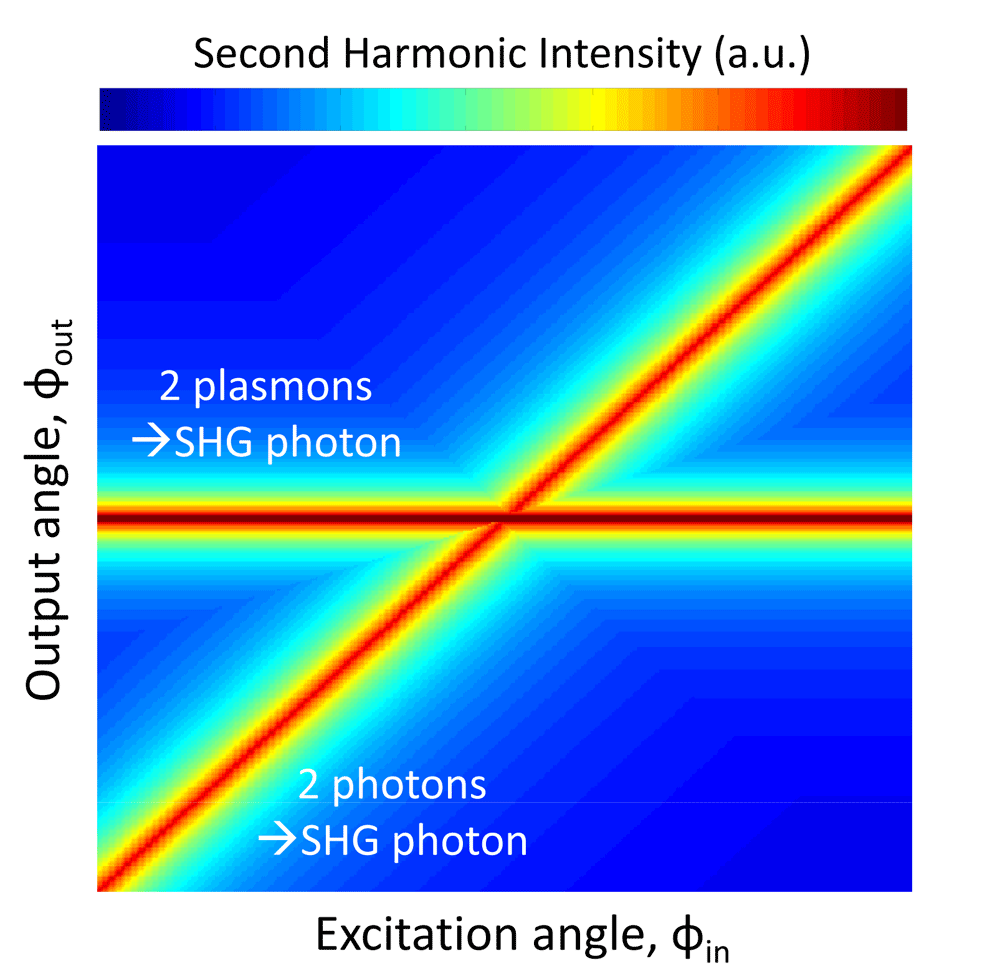
Theoretically, these momentum-conserving interactions can be distinguished on a dispersion diagram, which is a plot relating the second-harmonic output photon intensity to the input excitation angle and the output exit angle. For example, as illustrated in Fig. 2, two-photon interactions, $f (ω) + f (ω) \to f (2 ω)$ , mathematically map a diagonal line of positive slope on a dispersion diagram—as the input excitation angle is increased, so too is the second-harmonic exit angle. In contrast, plasmon-plasmon SHG interactions, $p (ω) + p (ω) \to f (2 ω)$ , map a straight line of zero slope: for all input excitation angles, only one exit angle will be allowed. Though not shown in the figure, the interaction for two photons generating a plasmon, $f (ω) + f (ω) \to p (2 ω)$ , follows a vertical line, because in the Kretschmann geometry, plasmons can only be excited for a very narrow range of input angles.

In a thorough and elegant experiment, Grosse and colleagues mapped such a dispersion diagram using a silver-on-prism setup similar to Simon’s [3] and a narrowly focused titanium-sapphire laser beam as a source. The intensity and angle of second-harmonic light reflected off a silver nanofilm was recorded as a function of input photon angle. As expected, their experimental dispersion results mapped a diagonal line, indicative of photon-photon interactions $[f (ω) + f (ω) \to f (2 ω)]$ . Intriguingly, their experimental dispersion diagram also revealed a horizontal line, indicative of plasmon-plasmon interactions $[p (ω) + p (ω) \to f (2 ω)]$ . In other words, some of the second-harmonic signal was emerging from two plasmons interacting with each other to form the second-harmonic photon.

The result is both beautiful and surprising. Until these experiments, many researchers would have expected plasmons to merely be catalysts of nonlinear processes. In that case, Grosse would only have observed a diagonal dispersion line. By also observing a horizontal dispersion line, Grosse’s momentum-resolved measurements provide evidence for the direct participation of surface plasmons in nonlinear phenomena. Specifically, the results demonstrate that SHG near a metal film can be enhanced because two individual photons, $f (ω)$ , each excite surface plasmons, $p (ω)$ , and subsequently, these plasmons radiatively recombine to form a higher-energy photon, $f (2 ω)$ .

Ultimately, these momentum-space measurements will enable exploration of the full gamut of nonlinear interactions. For example, such experiments could yield fundamental insight into the nature and mechanism of surface-enhanced Raman spectroscopy. Further, these results could enable design of new nanophotonic structures that greatly enhance the efficiency of nonlinear processes via plasmon-plasmon interactions. Lastly, these results could provide a pathway for creating entangled surface plasmon pairs, where one higher-energy photon is “down-converted” to two lower-energy plasmons. Such entangled plasmons could enable quantum optical computing on truly nanoscale dimensions. In this sense, Grosse and colleagues’ work demonstrates that a mirror’s reflection can, like the famous mirror in Snow White, indeed provide answers to many important, fundamental questions.

References

K. Kneipp, Y. Wang, H. Kneipp, L. T. Perelman, I. Itzkan, R. R. Dasari, and M. S. Feld, Phys. Rev. Lett. 78, 1667 (1997)
H. Atwater and A. Polman, Nature Mat. 9, 205 (2010)
N. B. Grosse, J. Heckmann, and U. Woggon, Phys. Rev. Lett. 108, 136802 (2012)
H. J. Simon, D. E. Mitchell, and J. G. Watson, Phys. Rev. Lett. 33, 1531 (1974)
P. Genevet, J.-P. Tetienne, E. Gatzogiannis, R. Blanchardt, M. Kats, M. Scully, and F. Capasso, Nano Lett. 10, 4880 (2010)
T. Trupke, M. Green, and P. Würfel, J. Appl. Phys. 92, 4117 (2002)
A. Atre and J. Dionne, J. Appl. Phys. 110, 034505 (2011)
Y. Nakayama, P. J. Pauzauskie, A. Radenovic, R. M. Onorato, R. J. Saykally, J. Liphardt, and P. Yang, Nature 447, 1098 (2007)

About the Author

Jen Dionne received her Ph.D. in applied physics in 2009 at the California Institute of Technology. After a postdoctoral research fellowship at the University of California, Berkeley, and Lawrence Berkeley National Laboratory, she arrived at Stanford University, where she is now an assistant professor of materials science and engineering. Her research investigates metamaterials—engineered materials with optical and electrical properties not found in nature—for applications ranging from high-efficiency solar energy conversion to bioimaging. In 2011, she was named one of Technology Review’s TR35—35 international innovators under 35 tackling important problems in transformative ways. She has also received the NSF CAREER Award (2012) and an AFOSR Young Investigator Award (2011).