Photons and Atoms Cooperate, Virtually

Ralf Röhlsberger

Viewpoint

Photons and Atoms Cooperate, Virtually

Deutsches Elektronen-Synchrotron DESY, Notkestrasse 85, D-22607 Hamburg, Germany

April 23, 2012• Physics 5, 46

Shifts in atomic energy levels caused by electron interaction with virtual photons can also occur in an ensemble of atoms acting cooperatively.

Figure caption — **Figure 1:** A focused laser beam (red) probes an ensemble of Rubidium atoms (yellow) confined between two windows of a vapor cell. The average distance of the atoms is smaller than the range of their dipole-dipole interaction (green sphere). Under these conditions the spectrally resolved transmission of the laser radiation reveals the collective Lamb shift of the atoms, shown in the bottom graph as function of the size of the atomic ensemble, defined by the distance $D$ of the windows (in units of the radiation wavelength).

The interaction of light with ensembles of many identical resonant atoms becomes increasingly relevant these days as more and more of such systems can be experimentally prepared in a controlled fashion, ranging from atoms in the gas phase, like Bose-Einstein condensates, to solid-state systems, like quantum dots. The existence of many identical resonators in close proximity modifies their properties to produce radiative and optical effects that do not occur in single atoms. A new cornerstone in the exploration of these effects has been laid by the work published in Physical Review Letters by James Keaveney at Durham University, UK, and colleagues [1]. Their results demonstrate how a phenomenon called the Lamb shift, which catalyzed the development of modern quantum field theory, can occur collectively in a group of atoms.

To put the work of Keaveney et al. into perspective, it is worthwhile to take a look at the single-atom Lamb shift. This effect was named after Willis Lamb, who first measured the relative shift of the $2 s_{1 / 2}$ and $2 p_{1 / 2}$ levels in atomic hydrogen; in Dirac theory, this shift should be zero. We know today that this shift mainly results from the emission and reabsorption of virtual photons by the same atom. Lamb won the Nobel prize in physics in 1955 for this work because it provided a fundamentally important stimulus: In the 1940s it was not clear how to get rid of divergencies in the calculation of the electromagnetic self-energy of a bound electron. The measurement by Lamb and Retherford [2] guided the theoretical efforts to handle these mathematical infinities in the right direction: First by Bethe, who applied a renormalization procedure to arrive close to the measured value of the hydrogen Lamb shift [3], then by Feynman, Schwinger, Tomonaga, and Dyson, who put this procedure forward into what we know today as quantum electrodynamics (QED), the fundamental theory of the interaction of light and matter.

The interaction of light and matter becomes more complex and richer in detail if many identical atoms are interacting with the same radiation field. This was realized first in 1954 by Robert Dicke, who studied the spontaneous emission from an ensemble of $N$ identical atoms and found the emission rate to be $N$ times faster than for a single atom, provided the atoms were confined in a volume of a size not larger than the wavelength ( $λ ≫ R$ ). This collective acceleration of the spontaneous emission is known as superradiance [4]. It prevails even in the limit of large samples ( $λ ≪ R$ ) that are excited by one resonant photon at a time. An impressive example for this type of superradiance is the collective resonant scattering of pulsed x rays from nuclear resonances of Mössbauer isotopes [5]. The Mössbauer effect ensures that x-ray photons interact recoillessly with atomic nuclei tightly bound in solids.

It took until 1973 to realize that not only real photons but also virtual photons have an impact on the collective interaction of light and matter, leading to a frequency shift of the emitted radiation. The collective Lamb shift (CLS) arises in the same way as the single-atom Lamb shift, except that the virtual photon is emitted by one atom and absorbed by another one in the ensemble [6,7]. In this sense the ensemble of resonant atoms can be considered a giant atom with a self-energy correction of its collective resonance energy due to virtual photon exchange. While the phenomenon of superradiance was observed and systematically explored rather soon after the invention of the laser, the CLS turned out to be very difficult to assess experimentally because of perturbing interactions in gases or solids of sufficiently high density whereupon the tiny radiative shift is completely buried. So far, the CLS has been observed in two experiments involving three-photon excitation in an atomic gas [8] and resonant x-ray scattering from Mössbauer nuclei embedded in a cavity [9]. Both experiments were performed in the large-sample limit ( $λ ≪ R$ ).

Because the CLS depends on the exchange of photons with other atoms in the ensemble, it is obvious that the magnitude of the shift depends on the spatial arrangement of the atoms. This was discussed in detail already by Friedberg et al. [6] and was followed then by a large body of theoretical investigations devoted to calculate the CLS for various spatial arrangements of the emitting atoms and different models for the electromagnetic field (see, e.g., Refs. [10,11] and references therein).

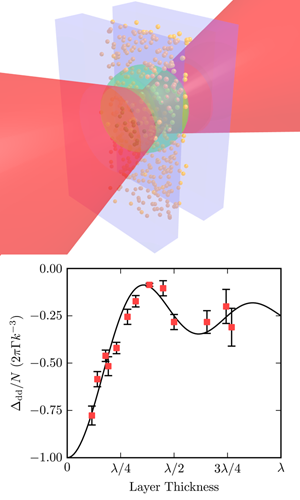
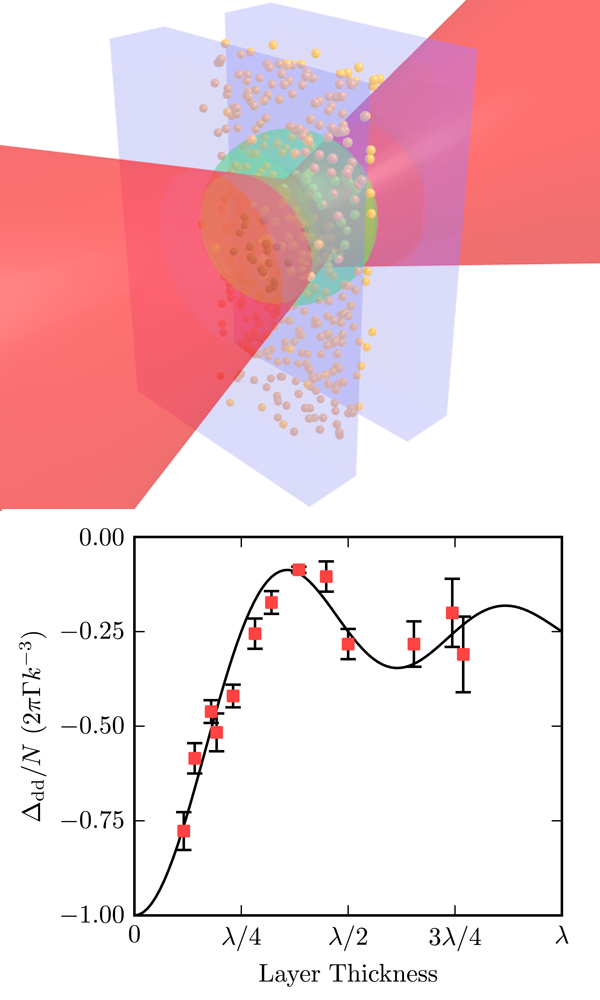
What remained elusive until the experiment of Keaveney et al. was the experimental confirmation of the predicted size dependence of the CLS. For transmission through a slab of resonant atoms with number density $ρ$ and thickness $D$ one expects a shift of the transition energy of

where the first term is a frequency shift due to the electrostatic dipole-dipole interaction induced by the radiation field, which is proportional to $ρ$ . The second term is the collective Lamb shift with its pronounced size dependence. Interference effects of the radiated photons within the extended sample lead to the oscillatory behavior described by the sinc function. The observation of this dependence poses a significant experimental challenge as it requires control of the thickness of the sample to within a fraction of the wavelength, i.e., well below $100$ nanometers (nm) to achieve a good resolution.

The authors managed this by confining a gaseous layer of rubidium atoms in a vapor cell with two windows that formed a wedge-shaped gap with thicknesses $D$ ranging from $30$ nm to about $2$ micrometers. The thickness of the gaseous sample could then easily be selected by transverse displacement of the vapor cell relative to the focused narrow-band laser beam traversing the cell. Transmission spectra were recorded by tuning the laser frequency across the rubidium D $2$ resonance at $λ = 780 nm$ . By varying the gas pressure, Keaveney and colleagues could easily adjust the density of the atoms in the vapor cell, thus achieving full control over the parameters that determine the CLS.

The result, illustrated in Fig. 1, is the first experimental confirmation of a prediction that was made almost $40$ years ago [6]. With this approach, the authors were able to extrapolate into the region where the thickness of the atomic layer goes to zero, a region that was completely inaccessible so far, and from which they could extract the dipole-dipole shift. Taking other contributions into account that arise from collisional broadening, Doppler effect, and cavity effects, the authors succeeded in explaining the measured transmission spectra (see Fig. 1) so that they could extract the frequency shift with high accuracy. The resulting dependence of the CLS on the thickness of the sample is very well described by the model that was developed almost $40$ years ago [6].

The experimental approach by Keaveney et al. is remarkable because it offers a new way to study this effect in a systematic fashion, with the potential to verify many of the theoretical predictions in connection with the CLS that have been made over the past four decades. Cooperative effects play an increasing role in current research in the optical sciences, with particular relevance for radiation transport in light-harvesting systems [12], localization of photons in disordered media [13], and quantum phase transitions [14], to name a few. Cooperative frequency shifts would even have to be taken into account in the development of ultraprecise frequency standards as they are discussed, e.g., to monitor the temporal change of fundamental constants.

From a fundamental point of view, collective Lamb-shift processes are an important ingredient in quantum-field theories of many-body systems. Therefore one can expect the paper to have far-reaching implications in diverse fields of the optical sciences and beyond.

References

J. Keaveney, A. Sargsyan, U. Krohn, I. G. Hughes, D. Sarkisyan, and C. S. Adams, Phys. Rev. Lett. 108, 173601 (2012)
W. Lamb and R. Retherford, Phys. Rev. 72, 241 (1947)
H. A. Bethe, Phys. Rev. 72, 339 (1947)
R. H. Dicke, Phys. Rev. 93, 99 (1954)
J. P. Hannon and G. T. Trammell, Phys. Rev. 186, 306 (1969)
R. Friedberg, S. R. Hartmann, and J. T. Manassah, Phys. Rep. C 7, 101 (1973)
M. O. Scully, Phys. Rev. Lett. 102, 143601 (2009)
W. R. Garrett, R. C. Hart, J. E. Wray, I. Datskou, and M. G. Payne, Phys. Rev. Lett. 64, 1717 (1990)
R. Röhlsberger, K. Schlage, B. Sahoo, S. Couet, and R. Rüffer, Science 328, 1248 (2010)
A. A. Svidzinsky, J. T. Chang, and M. O. Scully, Phys. Rev. A 81, 053821 (2010)
R. Friedberg and J. T. Manassah, Phys. Rev. A 84, 023839 (2011)
M. Sarovar, A. Ishizaki, G. R. Fleming, and K. B. Whaley, Nature Phys. 6, 462 (2010)
E. Akkermans, A. Gero, and R. Kaiser, Phys. Rev. Lett. 101, 103602 (2008)
K. Baumann, C. Guerlin, F. Brennecke, and T. Esslinger, Nature 464, 1301 (2010)

About the Author

Ralf Röhlsberger received his Ph.D. from the University of Hamburg. Following a postdoc appointment at the Advanced Photon Source, he was scientific assistant at the University of Rostock where he habilitated in 2002. In the same year he received the innovation award “Synchrotron Radiation” of BESSY (Germany). After an interim professorship at the Technical University of Munich, he has been a senior scientist at DESY in Hamburg since 2003 and was deputy leader of the Experimental Facility Division at the PETRA III synchrotron radiation source project. His research interests include the development of novel x-ray scattering methods, nuclear resonant scattering, physics of thin films, magnetic properties of low-dimensional systems, and x-ray quantum optics.