A Quantum Constellation

Qian Niu

Viewpoint

A Quantum Constellation

Department of Physics, The University of Texas at Austin, Austin, TX 78712-0264, USA
International Center for Quantum Materials, Peking University, Beijing, China

June 11, 2012• Physics 5, 65

Majorana’s geometrical representation of quantum spin as points on a sphere offers an intuitive approach to understanding quantum systems with multiple components.

Figure caption — **Figure 1:** (Left) In a spin- $1 / 2$ or other two-level system, any state can be built from a superposition of a spin-up and spin-down state (blue arrows). This superposition corresponds to a point on a unit sphere, defined by the vector $n$ . (Right) Planar projection of the north hemisphere of a spherical representation of Majorana stars for a spin $J = 25$ . The cloudy regions represent the probability distribution for the spin wave function. In Bruno’s picture, this probability distribution is analogous to the density of a classical gas that is repelled from the Majorana stars.

The Italian physicist Ettore Majorana, who disappeared in 1938, is now widely recognized for inventing the notion of a fermionic particle, the Majorana fermion, which has the strange property of being its own antiparticle [1]. What is perhaps less well known is that he also developed a natural and exact representation of a quantum spin [2], which inspired Julian Schwinger to create the bosonic representation often used today in the theoretical study of quantum spin systems [3].

In Majorana’s representation, a general spin state corresponds to a configuration of points on a sphere, a picture that makes a high dimensional Hilbert space easier to comprehend. In Physical Review Letters, Patrick Bruno of the European Synchrotron Radiation Facility in Grenoble, France, has revived this representation by developing an intuitive and systematic method for calculating the physical properties of the spin state, such as its energy, and following the spin’s evolution in time [4]. Bruno’s intuitive approach has the potential to guide our understanding of quantum systems with multiple components, which are vast and complex, yet increasingly, the focus of quantum engineering and quantum information.

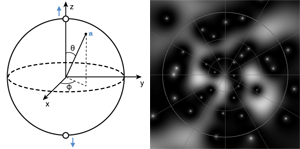
For the elementary case of a spin $1 / 2$ , or any quantum two-level system, Felix Bloch established [5] that an arbitrary pure state can be represented by a point on a unit sphere. In this picture (Fig. 1, left), a spin-up state corresponds to the north pole and a spin-down state corresponds to the south pole. A superposition of these two states corresponds to a point on the sphere, defined by the unit vector $n$ . The reason is geometrical: in addition to a nonessential normalization factor and an overall phase, a superposition state is specified by the relative amplitude and phase of its two components, and these two parameters can be mapped to the spherical coordinates $θ$ and $ϕ$ , which specify the direction of $n$ . The point at $n$ could equally well be viewed as an eigenstate with eigenvalue $+ 1 / 2$ for a spin oriented along $n$ . For this simple spin- $1 / 2$ case, the Majorana star is defined as the lone point on the sphere in the opposite direction to $n$ .

However, a spin- $J$ state with $J > 1 / 2$ , does not, in general, correspond to an eigenstate of the spin vector in any direction. In addition to an overall phase, it takes $2 J$ complex numbers to specify a state, and these numbers can’t be represented by a single point on a sphere. Eigenstates with eigenvalue $+ J$ for the spin component in each direction, which are called spin coherent states, constitute only a tiny subset of all possible quantum states. Nevertheless, one can represent a general quantum state as a linear superposition of the spin-coherent states. The superposition coefficient, given by the scalar product of the general state with a coherent state, is then a complex wave function of $n$ . Loosely speaking, this complex wave function represents the probability amplitude of finding the spin in that direction.

Majorana’s insight was that this wave function has $2 J$ points—or “vortices”—on the Bloch sphere where the wave function vanishes. Apart from an overall phase and normalization factor, the wave function is completely specified by the positions of these vortices. Specifically, the spin state has zero overlap with the spin coherent state along the directions of the vortices. In his new work, Bruno calls these vortices the Majorana stars. In this picture, the eigenstate of the spin angular momentum $m$ along direction $n$ corresponds to $m$ stars coinciding at – $n$ with the remaining $2 J - m$ stars coinciding at $n$ . Configurations other than these special “antipodal” distributions give all the other spin quantum states in the vast Hilbert space.

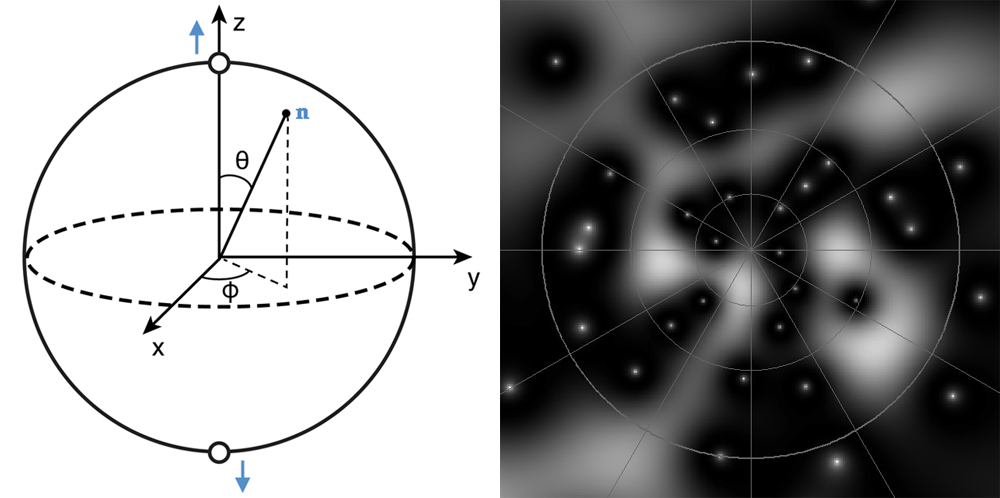
Bruno has found a systematic method of using diagrammatic rules to calculate the physical quantities, such as the energy, in terms of the Majorana star positions. The trick is to make a connection between the probability distribution of the spin wave function on the Bloch sphere and the density of a classical gas of independent particles (Fig. 1, right). Using this analogy, calculating the spin wave function is equivalent to calculating the distribution of the “gas” at thermal equilibrium, assuming it is repelled from the Majorana stars by a potential that varies logarithmically with distance. Moreover, Bruno has found that there is also an artificial magnetic field in the radial direction that has an intensity given by the gas density, as if each gas particle carries a quantum unit of magnetic flux. Together with the spin energy, this artificial magnetic field endows the Majorana stars with a classical dynamics that mirrors exactly the evolution of the quantum spin as governed by the Schrödinger equation.

As Bruno shows, Majorana stars are similar to vortices in other systems, such as a two-dimensional superfluid or an electron gas in a quantum Hall state. These vortices all have a life of their own, and feel an artificial magnetic field proportional to the particle density. There is a simple explanation of this common phenomenon. When a particle moves around a vortex once, the quantum wave function accumulates a phase of $2 π$ . In other words, the particle feels an Aharonov-Bohm-like flux at the vortex position. Since “moving around” is relative, one could look at this from the vortex’s perspective and say it feels the same flux at the particle. This is indeed confirmed in the present case by a direct calculation of the geometric phase for cyclic motion of the vortices [6].

The dynamics of the Majorana stars differs from, but is closely related to, the canonical form of the Hamiltonian dynamics that are taught in classical mechanics. A classical phase space is spanned by a set of generalized coordinates and their conjugate momenta, with velocities and forces simply given by the gradients of the Hamiltonian function. In the case of the quantum spin, the phase space is defined by the coordinates of the $2 J$ Majorana stars on the Bloch sphere, but the dynamics is in general noncanonical.

Had one chosen an orthogonal basis, such as the $2 J + 1$ eigenstates of the spin component along a fixed axis, the Schrödinger equation would imply a canonical dynamics, with the probabilities and phases playing the roles of canonical momenta and coordinates [7]. The canonical structure remains true even for the relative probabilities and phases after separating out the total probability (which is always normalized anyway) and a nonessential overall phase [8]. These canonical variables can be straightforwardly related to the Majorana stars, but the relation does not necessarily form a canonical transformation, rendering the dynamics of the latter noncanonical.

The Majorana representation and Bruno’s new development may turn out to be very useful in systems such as molecular magnets [9] or multilevel qubits [10]. Much of our intuition in the past was derived from a semiclassical picture, with the stars clustered together and moving according to the Landau-Lifshitz equation. Now we can visualize the quantum space in full detail and with ease by letting the stars spread out and wander on the Bloch sphere.

Acknowledgments

The author would like to acknowledge support from DOE-DMSE (DE-FG03-02ER45958), NBRPC (2012CB-921300), NSFC (91121004), and the Welch Foundation (F-1255).

References

F. Wilczek, “Majorana Returns,” Nature Phys. 5, 614 (2009)
E. Majorana, Nuovo Cimento 57, 43 (1932)
J. Schwinger, US Atomic Energy Commission, Report NYO-3071 (1952); later published in Quantum Theory of Angular Momentum, edited by L. C. Biendenharn and H. Van Dam (Academic Press, New York, 1965)
P. Bruno, Quantum Geometric Phase in Majorana’s Stellar Representation: Mapping onto a Many-Body Aharonov-Bohm Phase, Phys. Rev. Lett. 108, 240402 (2012)
F. Bloch and I. I. Rabi, “Atoms in Variable Magnetic Fields,” Rev. Mod. Phys. 17, 237 (1945)
See also J. H. Hannay, “The Berry Phase for Spin in the Majorana Representation,” J. Phys. A 31, L53 (1998)
A. Heslot, “Quantum Mechanics as a Classical Theory,” Phys. Rev. D 31, 1341 (1985)
J. Liu, B. Wu, and Q. Niu, “Nonlinear Evolution of Quantum States in the Adiabatic Regime,” Phys. Rev. Lett. 90, 170404 (2003)
P. C. E. Stamp, E. M. Chudnovsky, and B. Barbara, Quantum Tunneling of Magnetization in Solids, Int. J. Mod. Phys. B 6, 1355 (1992)
A. R. Usha Devi, Sudha, and A. K. Rajagopal, “Majorana Representation of Symmetric Multiqubit States,” arXiv:1103.3640

About the Author

Qian Niu is a Trull Centennial Professor of Physics at The University of Texas at Austin, from which he is currently on leave to serve as the director of the International Center for Quantum Materials at Peking University. He has worked on the theories on quantum Hall effects, quasicrystals, ultracold atoms, spin transport, and graphene materials, with an emphasis on topological and geometric phase effects in quantum transport. He obtained a B.S. from Peking University and a Ph.D. from the University of Washington at Seattle, and did postdoctoral work at the University of Illinois at Urbana-Champaign and the University of California at Santa Barbara before joining the faculty of UT Austin in 1990.