Not Every Exit is an Entrance

Gennady Shvets

Viewpoint

Not Every Exit is an Entrance

The University of Texas at Austin, Department of Physics, One University Station C1500, Austin, TX 78712, USA

July 16, 2012• Physics 5, 78

Experiments demonstrate a new way to prevent light from retracing its steps, which could potentially be integrated with other components on a chip to process optical information.

Figure caption — **Figure 1:** An optical isolator can be built on a chip using a waveguide that supports two optical modes, I and II, and a wave traveling in one direction with velocity $v$ . Downstream light, traveling from left to right in mode I (top), is unaffected by the traveling wave, but upstream light, traveling from right to left (bottom), is resonantly coupled into mode II and is therefore not injected back into the laser.

On a traditional computer chip, electric signals travel along metallic wires between various information-processing electronic components such as transistors arranged on an integrated circuit. One of the goals of high-performance computing is to move away from electric connections to optical connections. The reason is simple: light travels very fast and potentially without any losses en route. Developing such technologies will require developing sophisticated “optical plumbing” capable of delivering (or, better yet, producing), transporting, and modulating streams of photons on a chip. It is increasingly looking like all these developments are not too far in the future. Recent advances in nanofabrication have already produced an impressive range of ultracompact optical devices that can fit on a single computer chip.

The ever-expanding toolbox of integrated optics now includes photonic crystals, silicon waveguides and microrings, and waveguides integrated with plasmonic devices and even with graphene. With these tools, numerous on-chip optical devices have been developed, including delay lines, optical modulators, and nonlinear frequency converters, to name just a few. Still, one important optical component that has been missing from this impressive arsenal is the so-called nonreciprocal waveguide. Such a waveguide would allow photons, generated either on or off the chip by a laser source, to travel unperturbed in one direction (away from its source) but not in the opposite direction. Because reflected photons re-entering the laser source can destabilize it, it is imperative to isolate the source using such a nonreciprocal waveguide. In 2009, Zongfu Yu and Shanhui Fan at Stanford University, California, proposed a way to achieve such isolation [1], and now in Physical Review Letters, Hugo Lira and Michal Lipson at Cornell University, New York, work with them to demonstrate it experimentally [2].

Breaking propagation reciprocity is equivalent to breaking time-reversal symmetry, and several approaches have been used or proposed to do this. The most established is to use magneto-optical effects produced by a magnetic field. Because a magnetic field is produced by currents, which are reversed by the time-reversal operation, transparent magneto-optical materials enable nonreciprocal light propagation. Unfortunately, the magneto-optical effect is typically weak, so the commercial isolators based on it are bulky. Despite some progress in integrating magnetic garnets with semiconductor wafers, full chip-scale integration is still cumbersome because of the need for strong magnetic fields [3]. While the magneto-optical effects can be significantly enhanced by combining magneto-optical materials with metamaterial structures [4], practical devices based on this approach are yet to be demonstrated.

A second approach to evading time-reversal symmetry is to exploit material nonlinearity. Although reciprocity implies equal transmission for both propagation directions, light traveling in opposite directions in a device can still have different spatial intensity distributions. These differences, combined with material’s nonlinearity, induce direction-dependent nonlinear modifications of the refractive index and change the transmission in a nonreciprocal fashion. The most common drawback of most nonlinear schemes [5,6] is that high isolation and small insertion loss are achieved only for a limited range of back-reflection and input-laser intensities. These problems will likely be overcome in the future, as more advanced concepts [7,8] are realized. Nevertheless, the high laser powers required for nonlinearity-mediated nonreciprocal transmission are likely to limit the practical use of nonlinear isolators.

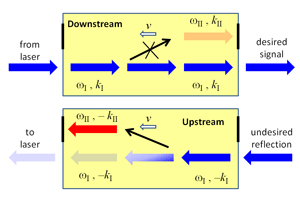
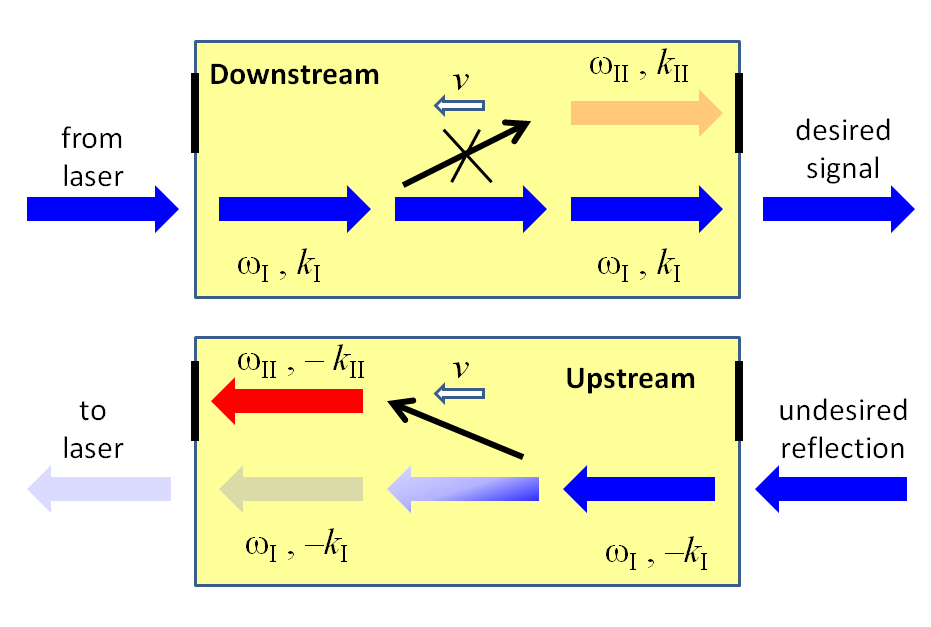
The third approach, taken by Lira et al., is the least common and, ironically, the easiest to understand and probably the most practical. It involves using a traveling wave (either electric or acoustic) with frequency $Ω$ and wave number $K$ , which breaks the time-reversal symmetry of the waveguide because it is traveling in a specific (for example, forward) direction with the phase velocity $ν = Ω / K$ . This approach requires a waveguide supporting at least two distinct modes (I and II) that are coupled to each other via a traveling-wave perturbation of the refractive index (Fig. 1). Light injected into mode I at frequency $ω_{I}$ and propagation constant $k_{I} (ω_{I})$ will resonantly couple to the mode II with frequency $ω_{II} = ω_{I} + Ω$ if the latter has the propagation constant $k_{II} (ω_{II})$ satisfying $k_{II} (ω_{II}) - k_{I} (ω_{I}) = K$ . As long as the propagation mismatch $Δ k \equiv k_{II} (ω_{I}) - k_{I} (ω_{I})$ between the two modes is small, the resonant matching condition can be expressed as

Here $v_{g}$ is the group velocity of mode II, which can be either positive or negative, depending on the direction of propagation. Because the absolute value of $Δ k / K$ does not change with the reversal of the propagation direction, Eq. (1) cannot be satisfied for both propagation directions unless the wave’s velocity is zero (corresponding to a static mode-coupling perturbation) or infinity (corresponding to a spatially-uniform time-dependent index perturbation).

The finite velocity $v$ of the index-perturbing wave thus creates an asymmetry between upstream and downstream wave propagation that can be used to convert upstream-propagating mode I into mode II without doing the same for the downstream-propagating modes. By analogy with solid-state systems, such time-dependent mode coupling has also been also referred to [1] as an indirect interband photonic transition. Very high isolation ratio (i.e., the ratio between downstream and upstream transmission) can, in principle, be achieved when the length of interaction between the two modes is chosen just right [1] to ensure complete mode conversion.

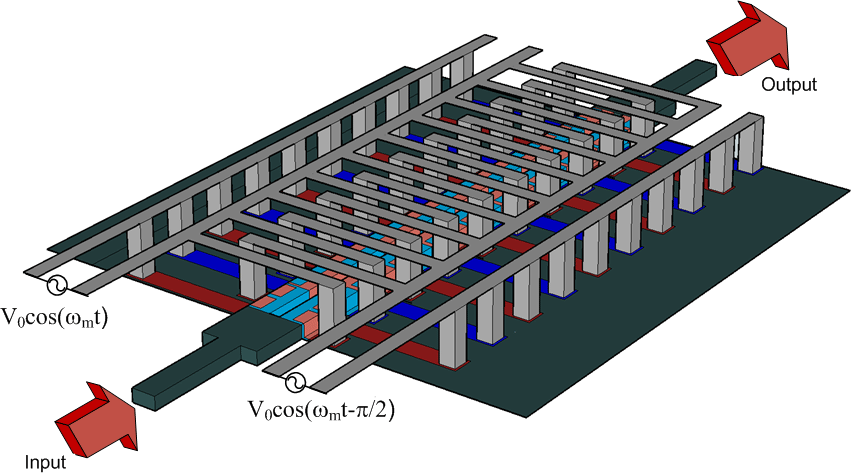
The photonic platform chosen by Lira et al. for demonstrating nonreciprocal mode conversion is a slotted waveguide supporting two modes: an even mode I, for which the field on the two sides is the same, and an odd mode II, for which the fields have opposite sign. Light injected from a single-mode waveguide naturally couples into the even mode of the slotted waveguide. To create a traveling-wave index perturbation, an array of pn-junction diodes was arranged inside the slotted waveguide with a periodicity $P = 2 π / K$ and fed by two phase-shifted microwave ( $Ω = 2 π \times 10$ gigahertz) transmission lines, as shown in Fig. 2. Light traveling in one direction remains in the even mode and couples out at the other end, but light traveling in the other direction transfers to the odd mode and is blocked. The measured isolation ratio between downstream and upstream transmission of infrared light in the telecommunications band was as high as a factor of $2$ $[$ $3$ decibels (dB)] when high enough microwave power was applied to the transmission line. Although only about one photon in ten million makes it through this demonstration device ( $70 dB$ insertion loss), the result provides an unambiguous proof of the principle of nonreciprocal propagation based on photonic mode conversion by a traveling refractive-index wave.

Practical implications of this fundamental result can be quite far-reaching, and may result in a chip-scale light isolator. While the isolation ratio of $3$ dB is still far below that of bulk magneto-optic commercial isolators ( $40 dB$ and higher) and lower than the $28 dB$ recently reported [8] for nonlinear chip-based isolators, Lira et al. report, based on their theoretical estimates, that this number can be considerably improved. A linear isolator can offer better pulse-shape preservation than a nonlinear one, which is critical for ultrashort pulse formats.

An important issue that will need to be addressed before traveling-wave silicon isolators become practical is the finite bandwidth. Because both $Δ k$ and $v_{g}$ are functions of the frequency, it follows from Eq. (1) that the resonance condition can be exactly satisfied for just one frequency. In practice, this implies that the optimal mode conversion of different frequency components of an ultrashort pulse would occur for different propagation distances, resulting in an incomplete optical isolation. This problem could potentially be addressed by using an adiabatically varying modulation period $P (z)$ along the propagation distance $z$ to enable mode conversion that does not depend on the length of the device [7]. Given the technological importance of nonreciprocal propagation, there is no doubt that a clever solution will eventually be found.

References

Z. Yu and S. Fan, “Complete Optical Isolation Created by Indirect Interband Photonic Transitions,” Nature Photon. 3, 91 (2009)
H. Lira, Z. Yu, S. Fan, and M. Lipson, ”Electrically Driven Nonreciprocity Induced by Interband Photonic Transition on a Silicon Chip,” Phys. Rev. Lett. 109, 033901 (2012)
L. Bi, J. Hu, P. Jiang, D. H. Kim, G. F. Dionne, L. C. Kimerling, and C. A. Ross, “On-Chip Optical Isolation in Monolithically Integrated Non-Reciprocal Optical Resonators,” Nature Photon. 5, 758 (2011)
A. B. Khanikaev, S. H. Mousavi, G. Shvets, and Y. S. Kivshar, “One-Way Extraordinary Optical Transmission and Nonreciprocal Spoof Plasmons,” Phys. Rev. Lett. 105, 126804 (2010)
K. Gallo, G. Assanto, K. R. Parameswaran, and M. M. Fejer, “All-Optical Diode in a Periodically Poled Lithium Niobate Waveguide,” Appl. Phys. Lett. 79, 314 (2001)
M. Soljačić, C. Luo, J. D. Joannopoulos, and S. Fan, “Nonlinear Photonic Crystal Microdevices for Optical Integration,” Opt. Lett. 28, 637 (2003)
S. Trendafilov, V. Khudik, M. Tokman, and G. Shvets, “Hamiltonian Description of Non-Reciprocal Light Propagation in Nonlinear Chiral Fibers,” Physica B 405, 3003 (2010)
L. Fan, J. Wang, L. T. Varghese, H. Shen, B. Niu, Y. Xuan, A. M. Weiner, and M. Qi, “An All-Silicon Passive Optical Diode,” Science 335, 447 (2012)

About the Author

Gennady Shvets received his Ph.D. in physics from the Massachusetts Institute of Technology in 1995. He is presently a Professor of Physics at The University of Texas at Austin, where he is pursuing research in several experimental and theoretical areas of optics, including metamaterials, nanoplasmonics, and interaction of ultraintense lasers with plasmas.