Seeing the “Quantum” in Quantum Zero-Point Fluctuations

Aashish Clerk

Viewpoint

Seeing the “Quantum” in Quantum Zero-Point Fluctuations

Aashish Clerk

Department of Physics, McGill University, Montréal, Québec H3A 2T8, Canada

January 17, 2012• Physics 5, 8

A technique from ion spectroscopy reveals the quantum nature of a mechanical system at low temperature.

Figure caption — **Figure 1:** (a) Canonical optomechanical system: a Fabry-Pérot cavity with a moveable mirror. The position $x$ of the mirror sets the cavity length, and hence the cavity frequency $ω_{M}$ . This mirror (which is attached to a fixed support via a spring) is in turn itself a mechanical system, with a vibrational frequency $ω_{M}$ . (b) Device used in the experiment: a patterned silicon nanobeam that supports both localized mechanical and optical resonances. (c) Optical power spectrum $S [ω]$ of light leaving the cavity in the case of a classical mechanical oscillator. The mechanical motion generates equal-area sidebands at frequencies $\pm ω_{M}$ from the laser frequency $ω_{L}$ . (d) Same, but in the quantum case. The sidebands no longer have equal weights, as zero-point mechanical motion cannot provide energy. Here, ${\bar{n}}_{M}$ is the number of mechanical quanta (due to non-zero temperature), and $x_{zpt}$ is the amplitude of the mechanical resonator’s zero-point motion.

Quantum zero-point motion, the fluctuation in the position of an object necessitated by the Heisenberg uncertainty principle, is among the most basic of quantum phenomena. While the origin of such fluctuations may be textbook material, unambiguously detecting them in a large mechanical structure (i.e., large compared to atomic scales) and, moreover, detecting their quantum nature, have remained elusive goals. These two tasks have now been accomplished by Amir Safavi-Naeini and co-workers at the California Institute of Technology in Pasadena [1]. As described in Physical Review Letters, this group coupled the motion of a patterned silicon nanomechanical beam to photons in an effective optical cavity formed in the beam. By laser cooling a mode of the beam’s motion to close to the quantum ground state, and by using a technique borrowed from ion-trap physics [2], they were able to clearly detect the quantum nature of the beam’s position fluctuations. This measurement of a truly nonclassical aspect of mechanical zero-point motion represents a milestone in the quest to measure and control the quantum nature of mechanical systems.

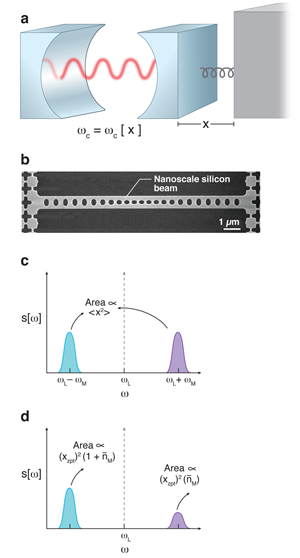
The system studied by Safavi-Naeini et al. is just one example of a cavity optomechanical system [3,4], where photons in an electromagnetic cavity are made to interact with a mechanical degree of freedom in a simple yet powerful way: the frequency of the cavity depends on the position of the mechanical element (Fig. 1). Mechanical oscillations at a frequency $ω_{M}$ will thus cause corresponding oscillations in the cavity frequency. If one then drives the cavity with a laser, the intracavity field will develop frequency-modulation sidebands at frequencies $\pm ω_{M}$ relative to the laser frequency, with weights that reflect the amplitude of the mechanical motion. For a mechanical oscillator behaving classically, the simple fact that the mechanical position $x (t)$ is always a well-defined real number guarantees that the two sidebands will have an equal weight. This is exactly what is observed by Safavi-Naeini et al. when the mechanical resonator is at a relatively high temperature, far from its ground state, and its position fluctuations are almost entirely thermal.

In contrast, as one approaches the mechanical ground state, zero-point fluctuations start to make a dominant contribution to the fluctuations of $x (t)$ . A crucial aspect of these fluctuations is that one cannot extract energy from them [5,6]. This simple fact leads to an asymmetry in the weights of the two mechanically generated sidebands when the mechanical resonator is cooled towards its ground state. The sideband at a frequency $ω_{M}$ above the laser frequency corresponds to the absorption of energy from the mechanical position fluctuations; it thus vanishes as one approaches the ground state. In contrast, the sideband at a frequency $ω_{M}$ below the laser frequency corresponds to the emission of energy to the mechanical resonator; it thus is present even in the ground state. We can thus think of zero-point fluctuations having only spectral weight at positive frequencies, not at negative frequencies, something that would be impossible if $x (t)$ were a classical, real-valued stochastic variable.

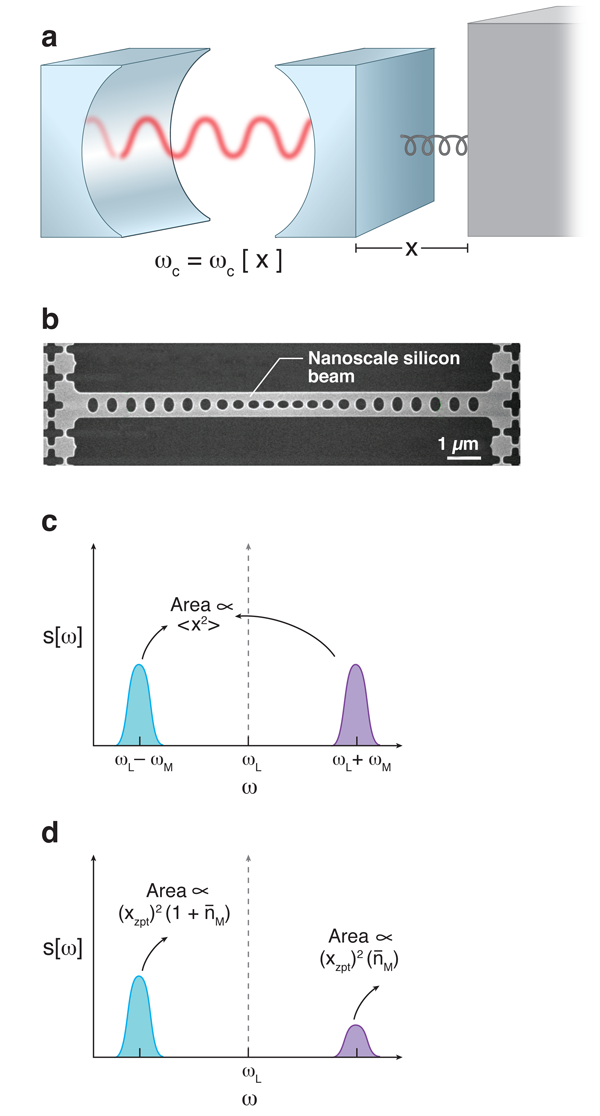
From the above discussion, it is clear that two conditions need to be satisfied in order to measure the quantum nature of mechanical zero-point motion: one must both cool the mechanical resonator to close to the ground state, as well as efficiently read out the mechanical motion in such a way that the two mechanically generated sidebands can be distinguished. In the work of Safavi-Naeini et al., the experimental setup involved a so-called optomechanical crystal [7], where a nanomechanical beam is patterned with holes in such a way that optical Bragg scattering yields localized optical resonances (which act as cavities), and acoustic Bragg scattering yields localized mechanical resonances. This approach yields relatively high-frequency mechanical resonances (with gigahertz-scale frequencies), which makes cooling easier and yields well-separated sidebands. The tight localization of modes also yields very strong optomechanical couplings. In addition, this setup allows a single mechanical resonance to be coupled to many distinct optical resonances. In the experiment, two such cavities were used: one for laser cooling the mechanical motion, the other for the readout of the motion. The motionally generated sidebands were measured by weakly driving the readout cavity with a laser, and looking at the power spectrum of the light transmitted past the cavity. By changing the frequency of the readout laser, the experimentalists could position either the lower or higher energy mechanical sideband to be at the cavity resonance, thus allowing efficient detection of both.

The experiment found a sideband asymmetry that increased with decreasing mechanical temperature, in excellent agreement with the predictions of quantum mechanics. At the lowest achieved temperature (corresponding to $2.6$ quanta in the mechanical mode), a maximum asymmetry of about $40 %$ was observed. Laser cooling of a mechanical mode to an occupancy of less than $1$ quanta was previously achieved by the Caltech team and collaborators from the University of Vienna using a similar device [8] and has also been achieved in optomechanical systems based on superconducting microwave circuits [9]; however, these experiments did not attempt to probe the mechanical zero-point noise by measuring a sideband asymmetry. Thus, unlike the most recent Caltech study, these previous experiments did not reveal any uniquely quantum features of the mechanical ground state (i.e., features apparent at even a qualitative level).

It is worth noting that related nonclassical physics was recently probed in an experiment by O’Connell and co-workers at the University of California, Santa Barbara (UCSB) [10], where a micron-scale piezoelectric mechanical resonator was resonantly coupled to a superconducting qubit. The UCSB team was able to move a single quanta between the qubit and resonator, convincingly demonstrating the quantization of energy in the mechanical resonator. In contrast to that work, the experiment by Safavi-Naeini et al. more directly reveals that the position fluctuations of the mechanical resonator at low temperatures cannot be described classically.

While this result may appear to just be a simple proof-of-principle, it does represent the first demonstration of truly quantum behavior of a mechanical element in an optomechanical system; it also demonstrates that such systems can be controlled and measured with sufficient care to reveal fragile quantum behavior. These are all prerequisites for more ambitious proposals to exploit quantum effects in these systems for applications in quantum information processing and ultrasenstive force detection. This experiment also suggests the exciting possibility of using optomechanical systems to study fundamental questions involving quantum noise physics in even more complex settings, for example, in the presence of nonlinearities generated by strong optomechanical couplings.

References

A. H. Safavi-Naeini, J. Chan, J. T. Hill, T. P. M. Alegre, A. Krause, and O. Painter, Phys. Rev. Lett. 108, 033602 (2012)
F. Diedrich, J. Bergquist, W. Itano, and D. Wineland, Phys. Rev. Lett. 62, 403 (1989)
T. Kippenberg and K. J. Vahala, Science 321, 1172 (2008)
F. Marquardt and S. M. Girvin, Physics 2, 40 (2009)
U. Gavish, Y. Levinson, and Y. Imry, Phys. Rev. B 62, 10637 (2000)
A. A. Clerk, M. H. Devoret, S. M. Girvin, F. Marquardt, and R. J. Schoelkopf, Rev. Mod. Phys. 82, 1155 (2010)
M. Eichenfield, J. Chan, R. M. Camacho, K. J. Vahala, and O. Painter, Nature 461, 78 (2009)
J. Chan, T. P. M. Alegre, A. H. Safavi-Naeini, J. T. Hill, A. Krause, S. Gröblacher, M. Aspelmeyer, and O. Painter, Nature 478, 89 (2011)
J. D. Teufel, T. Donner, D. Li, J. W. Harlow, M. S. Allman, K. Cicak, A. J. Sirois, J. D. Whittaker, K. W. Lehnert, and R. W. Simmonds, Nature 475, 359 (2011)
A. D. O’Connell, M. Hofheinz, M. Ansmann, R. C. Bialczak, M. Lenander, E. Lucero, M. Neeley, D. Sank, H. Wang, M. Weides, et al., Nature 464, 697 (2010)

About the Author

Aashish Clerk received an undergraduate degree in mathematics and physics from the University of Toronto in 1996, and a Ph.D. in physics from Cornell University in 2001. After carrying out postdoctoral research at Yale University, he joined McGill University in 2004 where he is now an associate professor of physics and a Canada Research Chair. His interests involve the theory of quantum noise and quantum measurements in quantum electronic systems, with a particular focus on quantum electromechanical and optomechanical systems, and superconducting circuits. He was awarded an Alfred P. Sloan fellowship in 2007.