Bringing the Sun Down to Earth

David Alexander

Viewpoint

Bringing the Sun Down to Earth

David Alexander

Department of Physics and Astronomy, Rice University, 6100 Main St, Houston, TX 77005, USA

August 13, 2012• Physics 5, 90

A laboratory analog of solar plasma offers a new tool in the search for the origin of coronal heating.

Figure caption — **Figure 1:** Magnetically confined plasma structures—on the sun and in the lab. (a) Magnetic arches in the solar corona. The structures are axially collimated over several layers in the Sun’s atmosphere, even though the densities of the layers vary greatly. (b) Stenson and Bellan’s experiment. Hydrogen gas is confined in a magnetic fluxtube shortly after the tube forms. The structure is axially collimated, as in actual coronal magnetic structures. (c) Schematic of the forces that cause collimation in a magnetic flux tube, as seen from above the arch. In a typical dipole field, the field lines spanning the two poles would bow out, but in the coronal structures, the existence of a magnetic field azimuthal to the main field lines generates a $J \times B$ force that pushes plasma flow towards the less constricted regions. These flows also transport azimuthal flux from the stronger field regions resulting in a dynamic collimation of the structure.

The sun is often portrayed as a “laboratory for astrophysics” but it is a laboratory over which we have no control. Instead, solar physicists employ a wide range of theoretical, computational, and observational tools to study the magnetically driven activity on the sun. The challenge for these methods is that solar physics is extremely complex, making it difficult to isolate the key drivers of any one phenomenon.

All of this is changing with the development of tailored, laboratory-scale plasma experiments here on earth. In Physical Review Letters, Eve Stenson and Paul Bellan at the California Institute of Technology in Pasadena describe just such an experiment [1], which is aimed at understanding a long-standing puzzle: why the solar corona—the halo of plasma that surrounds the sun’s atmosphere—is so hot. In their setup, they inject ionized gas into a horseshoe-shaped magnetic field, allowing them to simulate the dynamic behavior of plasma confined by the arched magnetic fields associated with sunspots. These fields are believed to play an important role in providing the energy to heat the corona, but the mechanism by which this occurs has been unclear. By demonstrating that they can create, within a plasma, magnetic fields with roughly the same shape and properties as those found in the corona, Stenson and Bellan offer an exciting opportunity to see solar magnetic forces at work in a controllable experiment.

In the 1930s, scientists observing the solar corona found a mysterious spectroscopic line that was emitted from highly ionized iron. The finding revealed that the solar corona was a few million degrees kelvin, more than three hundred times hotter than the surface of the sun below, and flew in the face of what was expected from simple thermodynamics [2]; namely, that the corona, being furthest from the heat generated by nuclear fusion at the sun’s core, should be cooler than the underlying layers. For the next 80 years, solar physicists tried to understand what was making the corona so hot.

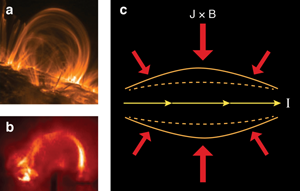
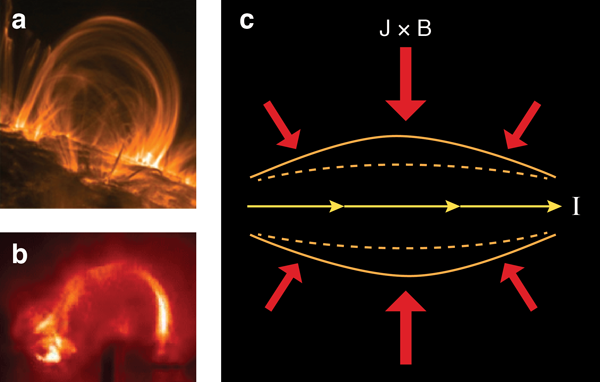
It is now universally accepted that the reservoir of energy stored in the sun’s atmospheric magnetic field is what heats the localized plasma in the corona. In simplified terms, the field is generated in the solar interior as a result of large-scale rotational and convective motions of the charged plasma, which serve to produce a strong ( $100, 000$ gauss) magnetic field some $200, 000 km$ below the solar surface [3]. At this depth, the field is in the form of a concentrated tube that encircles the sun, but as it makes its way to the surface, it can emerge as a pair, or group, of sunspots connected by arches of magnetic field that extend hundreds of thousands of kilometers into the solar atmosphere [Fig. 1(a)]. These arched fields vary in strength from $2$ – $3$ kilogauss (kG) at either foot, to about $10$ – $100$ gauss (G) at their apex.

What is not known, and remains under considerable debate even now, is how the energy stored in the magnetic fields is converted into heating the corona [4]. Several authors have argued that the corona itself is not directly heated, but is a consequence of energy released in the much cooler chromosphere ( $\sim 50, 000 K$ )—a highly dynamic region of the solar atmosphere that separates the corona from the sun’s surface (photosphere)—that both heats the chromospheric plasma to coronal temperatures and then drives the heated plasma into the corona along the preexisting arched magnetic fields [5]. As an explanation, this idea has some advantages in that the energy dissipation is more efficient in the dense chromosphere and more naturally explains the density of the coronal material confined by the magnetic arches, which is much higher than that of the background corona. The drawback is we are left needing to understand the dissipation process, how the plasma is transported to the corona, and the impact on the preexisting magnetic field.

Another puzzle is the shape of the coronal magnetic arches. The observed structures have a much more uniform (collimated) width across their entire length than would be expected from a simple dipolar field extending over such a great height.

To understand the forces at work in these magnetic structures, simulations, such as those by Stenson and Bellan, have to create, as well as possible, the particular properties of coronal plasma. First, it is a fully ionized, highly conductive medium with a temperature of $\sim 2$ – $4$ million degrees kelvin and a density of roughly $10^{14}$ – $10^{15} m^{- 3}$ . Second, the plasma predominantly flows along the field lines and only negligibly across them. Third, the dominance of the magnetic field in the solar corona is captured by the values of two dimensionless parameters that characterize magnetized plasmas: a magnetic Reynolds number (the ratio of magnetic flow to magnetic diffusion in the plasma) of $10^{12 - 14}$ and a plasma beta (the ratio of the plasma pressure to the magnetic pressure) of $≪ 1$ . In plasma with these properties, the magnetic field is able to provide the energy to heat the plasma and drive it dynamically while confining it to the structured magnetic fluxtubes observed to make up the solar corona. It is the ability to create a plasma with dimensionless quantities similar in value to those in the solar corona that allows one to extrapolate from a 1 m laboratory scale to the $100, 000 km$ scale of the solar atmosphere.

To mimic the magnetic structures found in the solar corona, Stenson and Bellan use a pair of magnetic field coils that are pulsed to generate a current-free magnetic field within a $1.4$ - $m$ -long vacuum chamber. The field varies from $3.5 kG$ at its base to about $100 G$ at its apex. The plasma is comprised of a neutral gas (hydrogen, nitrogen or argon) that is ionized at the injection point by a high-voltage capacitor. With this experimental setup, plasma densities of $\sim 10^{20 - 21} m^{- 3}$ and a beta $≪ 1$ are achieved. This is denser than the plasma in the solar corona, but has the same important property in that it is the field that dominates the plasma.

The authors demonstrate that some fundamental plasma physics processes associated with the presence of a strong guiding field and field aligned currents naturally lead to plasma flows into the large-scale arched field [Fig. 1(b)], with a magnitude comparable to what is observed in the solar atmosphere. These flows, in turn, result in a collimated lengthening of the magnetic structure similar to what is seen in solar observations. Specifically, the experiment confirms that it is the so-called hoop force, in which the magnetic structure acts on itself via the Lorentz force ( $J \times B$ ), that explains the observed lengthening of the magnetic arches, while the other components of the $J \times B$ force, together with the pressure gradients, serve to drive the plasma and flux along the magnetic field and maintain a highly collimated plasma structure [Fig. 1(c)]. The hoop force is well known in laboratory plasma physics [1], but because the conditions in the solar atmosphere vary greatly, it has been difficult to compare experiments with observations. The Stenson and Bellan work, then, is a significant advance in modeling an astrophysical process and, in particular, of our understanding of the dynamical nature of the solar atmosphere and how it is mediated by the magnetic field.

Laboratory simulations of solar plasma are useful, but interpreting them requires caution. While the experiments have many features in common with the solar regime—low plasma beta, high conductivity, comparable flow velocities—the spatial and temporal scales of the system are vastly different and, in the case of Stenson and Bellan’s experiment, the required currents responsible for the various forces, and the relationship of this current to the other parameters of the system, may not directly scale to the equivalent solar conditions [6]. In the authors’ experiment, the magnetic loops eventually develop a kink, suggesting the current running through them has become too large for the field to remain in equilibrium, i.e., it has become supercritical and an instability develops [7]. On the sun, kinking structures are not uncommon but rarely represent the standard active region of the corona that is the focus of these simulations. Future experiments examining the role of the current would therefore be interesting.

The importance of laboratory-scale experiments was recently recognized by the American Astronomical Society, which created the Laboratory Astrophysics Division, the Society’s first new division in over $30$ years. The laboratory confirmation that specific plasma physics phenomena, in this case, common magnetohydrodynamics forces, are providing complex physical behavior in magnetic structures, similar to that seen on the sun, is extremely exciting. They will help frame the discussion for our attempts to understand the wide range of phenomena that constitute solar activity.

References

E. V. Stenson and P. M. Bellan, ”Magnetically Driven Flows in Arched Plasma Structures,” Phys. Rev. Lett. 109, 075001 (2012)
H. A. Bodin and B. E. Keen, “Experimental Studies of Plasma Confinement in Toroidal Systems,” Rep. Prog. Phys. 40, 1415 (1977)
D. Alexander, The Sun (Greenwood Press, Santa Barbara, 2009)[Amazon][WorldCat]
C. H. Mandrini, P. Démoulin, and J. A. Klimchuk, “Magnetic Field and Plasma Scaling Laws: Their Implications for Coronal Heating Models,” Astrophys. J. 530, 999 (2000)
M. J. Aschwanden, “An Evaluation of Coronal Heating Models for Active Regions Based on Yohkoh, SOHO and TRACE Observations,” Astrophys. J. 550, 1036 (2001)
D. D. Ryutov and B. A. Remington, “Scaling Laws for Collisionless Laser Plasma Interactions of Relevance to Laboratory Astrophysics,” Astrophys. Space Sci. 307, 291 (2007)
T. Török, M. A. Berger, and B. Kliem, “The Writhe of Helical Structures in the Solar Corona,” Astron. Astrophys. 516, 49 (2010)

About the Author

David Alexander is a professor in the Department of Physics and Astronomy at Rice University and Director of the Rice Space Institute. He received a Presidential Early Career Award for Scientists and Engineers in 2004 and was appointed a Kavli Frontiers Fellow by the National Academy of Sciences in 2006. He is currently the Chair of the Solar Physics Division of the American Astronomy Society and Chair of the Solar Heliospheric Interplanetary Environment (SHINE) program. Professor Alexander has served on many national and professional committees including the NASA Advisory Council’s Heliophysics Subcommittee and the Science Advisory Board of the High Altitude Observatory Coronal Solar Magnetism Observatory. He is author of The Sun, part of the Greenwood Press “Guide to the Universe” series.