A New Look at the Hydrogen Wave Function

Christopher  T. L. Smeenk

Viewpoint

A New Look at the Hydrogen Wave Function

Joint Attosecond Science Laboratory, University of Ottawa and National Research Council of Canada, Ontario K1A 0R6, Canada

May 20, 2013• Physics 6, 58

A newly-developed “quantum microscope” uses photoionization and an electrostatic magnifying lens to directly observe the electron orbitals of an excited hydrogen atom.

Figure caption — **Figure 1:** A photoionization microscope provides direct observation of the electron orbital of a hydrogen atom. The atom is placed in an electric field $E$ and excited by laser pulses (shown in blue). The ionized electron can escape from the atom along direct and indirect trajectories with respect to the detector (shown on the far right). The phase difference between these trajectories leads to an interference pattern, which is magnified by an electrostatic lens.

The wave function plays a fundamental role in quantum theory, yet a direct observation of it remains elusive. Observable properties, such as the position of an atom or the momentum of an electron, arise from projecting the wave function onto an eigenstate. However, each projection only reveals a portion of the underlying wave function and often destroys uniquely quantum features, like superposition and entanglement. The full quantum state is only realized by statistically averaging over many measurements. A tool that directly magnifies the microscopic state of a quantum particle onto the laboratory scale could, potentially, render some quantum properties directly perceptible. More practically, such a quantum microscope could aid development of atomic and molecular-scale technologies.

Writing in Physical Review Letters, Aneta Stodolna, of the FOM Institute for Atomic and Molecular Physics (AMOLF) in the Netherlands, and her colleagues demonstrate how photoionization microscopy directly maps out the nodal structure of an electronic orbital of a hydrogen atom placed in a dc electric field [1]. This experiment—initially proposed more than $30$ years ago—provides a unique look at one of the few atomic systems that has an analytical solution to the Schrödinger equation. To visualize the orbital structure directly, the researchers utilized an electrostatic lens that magnifies the outgoing electron wave without disrupting its quantum coherence. The authors show that the measured interference pattern matches the nodal features of the hydrogen wave function, which can be calculated analytically. The demonstration establishes the microscopy technique as a quantum probe and provides a benchmark for more complex systems.

Methods for imaging a wave function are often indirect. One such strategy involves making many so-called weak measurements of a quantum system, in order to tiptoe around wave function collapse [2]. Alternatively, a series of strong measurements on identically prepared systems can be used to reconstruct the quantum state. For example, researchers have mapped out the complete quantum state of photons and other fields by making a series of measurements in different bases and then inverting those results through a tomographic procedure [3]. Tomographic inversion, which, in general, involves generating an image from a set of projections, has proven useful in other experiments as well. For example, one group used high-harmonic XUV spectra to reconstruct the valence electron wave function in $N_{2}$ [4], while another group used angle-resolved photoelectron emission spectra to reconstruct the orbitals of molecules on a thin film [5]. All of these experiments combine a series of partial views of the quantum system to reconstruct the wave function.

More direct methods also exist, in which elements of the wave function appear in a single measurement. Scanning tunneling microscopy of molecules on a thin film, for example, has provided images of the nodal structure in molecular orbitals [6]. More recently, measurements of outgoing electrons from multiphoton ionization of molecules showed evidence of nodal planes in molecular orbitals [7]. In these photoionization studies, researchers can select and/or manipulate the molecules using static fields or laser techniques to control or induce a dipole. However, measuring the nodal structures of atomic orbitals is more challenging, since atoms don’t have a dipole or external degrees of freedom. Stodolna et al. overcome this by applying a dc electric field that defines a quantization axis in hydrogen and aligns the orbitals before measuring them. This allows direct observation of the transverse orbital state, which is the projection of the orbital onto the plane perpendicular to the electric field.

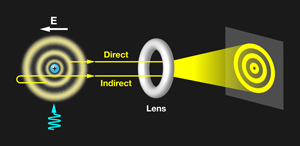
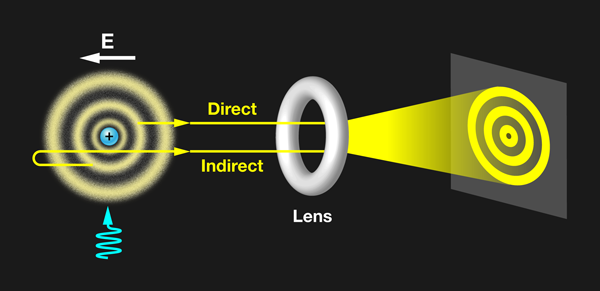
In their elegant experiment, Stodolna et al. observe the orbital density of the hydrogen atom by measuring a single interference pattern on a 2D detector (see Fig. 1). This avoids the complex reconstructions of indirect methods. The team starts with a beam of hydrogen atoms that they expose to a transverse laser pulse, which moves the population of atoms from the ground state to the $2 s$ and $2 p$ orbitals via two-photon excitation. A second tunable pulse moves the electron into a highly excited Rydberg state, in which the orbital is typically far from the central nucleus. By tuning the wavelength of the exciting pulse, the authors control the exact quantum numbers of the state they populate, thereby manipulating the number of nodes in the wave function. The laser pulses are tuned to excite those states with principal quantum number $n$ equal to $30$ .

The presence of the dc field places the Rydberg electron above the classical ionization threshold but below the field-free ionization energy. The electron cannot exit against the dc field, but it is a free particle in many other directions. The outgoing electron wave accumulates a different phase, depending on the direction of its initial velocity. The portion of the electron wave initially directed toward the 2D detector (direct trajectories) interferes with the portion initially directed away from the detector (indirect trajectories). This produces an interference pattern on the detector. Stodolna et al. show convincing evidence that the number of nodes in the detected interference pattern exactly reproduces the nodal structure of the orbital populated by their excitation pulse. Thus the photoionization microscope provides the ability to directly visualize quantum orbital features using a macroscopic imaging device.

To confirm this interpretation, the authors de-tuned the excitation laser pulse from the excited state. Under these conditions, the excited electron is still a free particle, but it does not acquire the characteristic nodal structure of the quasibound Rydberg orbital. Under nonresonant conditions the interference pattern disappeared and was replaced by an isotropic background contribution. The appearance of nodal features only under resonant excitation solidifies the interpretation that the detected interference pattern is generated by the quantum state selectively populated.

The present work on the hydrogen atom clearly illustrates how the photoionization microscope images an electron orbital. In contrast, the authors’ previous work with photoionization microscopy found that orbital information can be obscured by multielectron effects [8]. Future research will try to understand how the electron-electron interaction manifests in photoionization microscopy. Further nuances could be investigated by introducing a magnetic field to perturb the outgoing electron wave function. On this front there are already proposals for applying photoionization microscopy to investigate chaotic motion in quantum systems [9], and the Ahronov-Bohm effect [8]. More generally, the development of a quantum microscope that can image orbital features could aid atomic and molecular scale technologies, for example, by visualizing the nature of the chemical bond binding a molecular wire [10].

References

A. S. Stodolna, A. Rouzée, F. Lépine, S. Cohen, F. Robicheaux, A. Gijsbertsen, J. H. Jungmann, C. Bordas, and M. J. J. Vrakking, “Hydrogen Atoms under Magnification: Direct Observation of the Nodal Structure of Stark States,” Phys. Rev. Lett. 110, 213001 (2013)
J. S. Lundeen, B. Sutherland, A. Patel, C. Stewart, and C. Bamber, “Direct Measurement of the Quantum Wavefunction,” Nature 474, 188 (2011)
A. I. Lvovsky and M. G. Raymer, “Continuous-Variable Optical Quantum-State Tomography,” Rev. Mod. Phys. 81, 299 (2009)
J. Itatani, J. Levesque, D. Zeidler, H. Niikura, H. Pepin, J. C. Kieffer, P. B. Corkum, and D. M. Villeneuve, “Tomographic Imaging of Molecular Orbitals,” Nature 432, 867 (2004)
P. Puschnig, S. Berkebile, A. J. Fleming, G. Koller, K. Emtsev, T. Seyller, J. D. Riley, C. Ambrosch-Draxl, F. P. Netzer, and M. G. Ramsey, “Reconstruction of Molecular Orbital Densities from Photoemission Data,” Science 326, 702 (2009)
J. Repp, G. Meyer, S. M. Stojković, A. Gourdon, and C. Joachim, “Molecules on Insulating Films: Scanning-Tunneling Microscopy Imaging of Individual Molecular Orbitals,” Phys. Rev. Lett. 94, 026803 (2005)
L. Holmegaard et al., “Photoelectron Angular Distributions from Strong-Field Ionization of Oriented Molecules,” Nature Phys. 6, 428 (2010)
F. Lépine, Ch. Bordas, C. Nicole, and M. J. J. Vrakking, “Atomic Photoionization Processes under Magnification,” Phys. Rev. A 70, 033417 (2004)
L. Wang, H. F. Yang, X. J. Liu, H. P. Liu, M. S. Zhan, and J. B. Delos, “Photoionization Microscopy of the Hydrogen Atom in Parallel Electric and Magnetic Fields,” Phys. Rev. A 82, 022514 (2010)
L. Grill, M. Dyer, L. Lafferentz, M. Persson, M. V. Peters, and S. Hecht, “Nano-Architectures by Covalent Assembly of Molecular Building Blocks,” Nature Nanotech. 2, 687 (2007)

About the Author

Christopher Smeenk is a postdoctoral researcher in the Department of Physics at University of Ottawa and the Joint Attosecond Science Lab at National Research Council in Ottawa, Canada. His research focuses on applications of ultrashort laser pulses to control and image matter on the atomic and molecular scale.