To Screen or Not to Screen, That is the Question!

Romain Maurand; Christian Schönenberger

Viewpoint

To Screen or Not to Screen, That is the Question!

Romain Maurand and Christian Schönenberger

Department of Physics, University of Basel, CH-4056 Basel, Switzerland

July 1, 2013• Physics 6, 75

Using a tunneling probe, physicists observe transitions in a quantum dot that imply screening of a magnetic impurity by a nearby superconductor.

Figure caption — **Figure 1:** (a) A singly occupied quantum dot, shown with the circle to the left, acts as a spin- $1 / 2$ impurity. Once well coupled to a normal electrode $N$ , the spin on the dot (blue arrow) can be screened by the spins (red arrows) of the conducting electrons present at the Fermi level of the contact. (b) When the singly occupied quantum dot is coupled instead to a superconducting electrode $S$ , the screening problem becomes complex. In a superconductor, electrons with antiparallel spin are paired to form Cooper pairs, which cannot screen the spin- $1 / 2$ impurity on the dot. The system will then have to choose between an unscreened QD with an undisturbed superconductor or a screened QD with a disturbed superconductor.

Impurities complicate the physics of a pure system and may therefore be seen as a nuisance. But history has often demonstrated that impurities in materials reveal unexpected phenomena leading to novel applications. Dopants in semiconductors, for example, led to transistors, and color centers in dielectrics made possible solid-state lasers. Now physicists are complicating things again by introducing magnetic impurities into superconductors. These hybrid structures might potentially be used to produce entangled electrons or to form electronic quasiparticles that act as their own antiparticles. But before any truly useful devices can be made, a better understanding is needed of the impact that the magnetic impurity has on the superconductor.

Writing in Physical Review B [1], Jean-Damien Pillet of the Atomic Energy Commission (CEA) in Gif-sur-Yvette, France, and his colleagues address the complex problem of a magnetic impurity inside a superconductor by using an artificial atom—a so-called quantum dot (QD)—coupled to superconducting electrodes. In this case, the QD is a section of a carbon nanotube, but previous experiments have used other types of QDs, such as semiconducting nanowires and self-assembled QDs [2]. The electronic spectrum of a QD consists of discrete levels similar to an atom. But unlike a real atom, the filling of a QD with electrons is controllable with a gate voltage. This tunability makes a QD system a very versatile platform to explore the physics of magnetic impurities coupled to a normal metal or superconductor. Of particular interest is a QD hosting exactly one electron. In this situation, the electron can be either spin up or spin down, so the QD acts as a twofold degenerate spin- $1 / 2$ impurity, a so-called doublet.

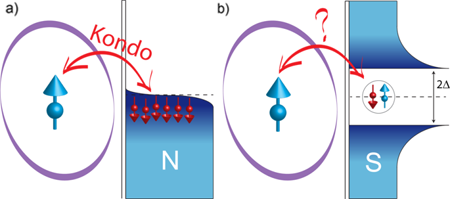
The presence of a spin- $1 / 2$ impurity produces changes in electric transport, both in metallic and superconductor hosts. This intriguing physics arises out of the host material attempting to negate, or screen out, the effect of the impurity. In the metallic environment, so-called exchange processes can take place between the conduction electrons and the spin- $1 / 2$ impurity. Each exchange process effectively flips the spin of the impurity from up to down, or vice versa. These processes occur over and over with many different conduction electrons, which together screen the impurity [see Fig. 1(a)]. This many-electron exchange interaction, known as the Kondo effect, places the impurity in a singlet ground state, whose energy is lower by the exchange term $E_{x}$ than the initial doublet ground state. The Kondo effect produces a signature in the electronic spectral density in the form of a resonance peak at the Fermi energy [3]. The normal-state Kondo effect of a spin- $1 / 2$ impurity is very well understood today.

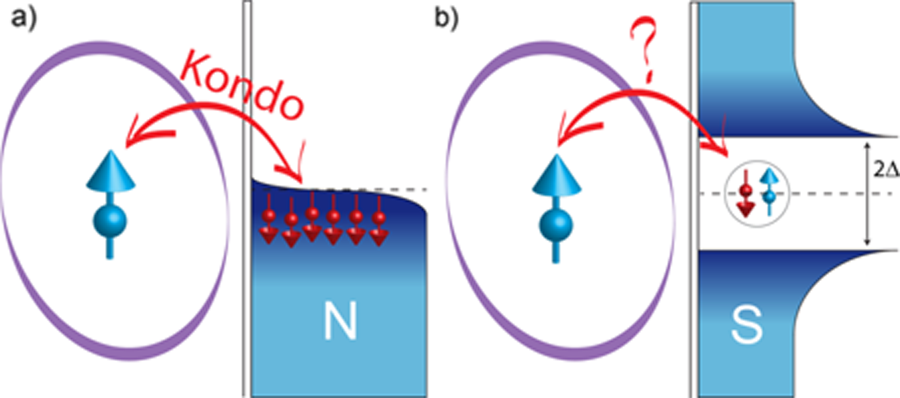
In the superconducting state, however, the spin- $1 / 2$ impurity problem is much more complex [4]. Different from a normal metal, the superconductor already has a many-body ground state to begin with. Indeed, below the superconductor’s critical temperature, electrons with opposite spins pair up into spin singlets known as Cooper pairs, thereby gaining a pairing energy of $2 Δ$ . This pairing, which occurs between electrons with energies near the Fermi energy, produces a window of size $2 Δ$ in the density of states, where no free electrons are available anymore. Since a Cooper pair has no net spin, it cannot screen the spin- $1 / 2$ magnetic impurity. The system has to choose either to “soften” the pairings so that free electrons are available to screen the impurity, or to keep the pairings and let the impurity go unscreened [see Fig. 1(b)] [5]. Screening is preferred if the gain in exchange energy is larger than the pairing energy, i.e., if $E_{x} > 2 Δ$ .

Previous studies have observed the competition between screening and nonscreening using a variety of different methods. For example, tuning the coupling between the local impurity and the electrode can provide information about the screening [6]. Another signature of the screening competition comes from the dissipationless current (supercurrent) through a superconductor-QD-superconductor (S-QD-S) junction [7]. The nonscreening of the spin- $1 / 2$ impurity forces a reversal of the supercurrent. A careful analysis of where the supercurrent is reversed has even allowed the construction of a phase diagram of the ground state, in which a (quantum) phase transition occurs between the screened and unscreened impurity [7]. Inducing this transition is possible through changes in the microscopic parameters, such as the charging energy on the impurity site and the coupling strength between the impurity and the superconductors.

More recently, Pillet et al. demonstrated the possibility of measuring the local spectroscopy of a carbon nanotube QD coupled to two superconducting electrodes [8]. For that purpose, they connected a weakly coupled electrode to the carbon nanotube QD. This third electrode plays the role of a tunnel probe through which tunneling spectroscopy is performed. Since electrons tunnel at finite energy through the QD, this spectroscopy reveals the electronic transitions at the impurity site from the ground state to the excited state with the same filling of electrons. If the spin- $1 / 2$ impurity is screened, the ground state is a singlet state and the excited state is a doublet. The opposite is true in the unscreened case, with a ground-state doublet and excited singlet. The evolution of the spectroscopic transition as a function of QD parameters can reveal the ground-state properties of the impurity.

In this latest effort [1], Pillet et al. carefully measured the transition energies and managed to deduce the coupling strength from the spin- $1 / 2$ impurity to the superconducting electrode and to predict the Kondo resonance expected in the normal state. These measurements demonstrate the level of understanding that could be achieved for this complex problem today. More than giving a microscopic insight into the interplay between superconductors and a magnetic impurity, the direct spectroscopy of a nanostructure appears as a perfect tool to explore even more complex superconducting nanostructures. For instance, spectroscopic analysis might provide a clearer understanding of Majorana fermions (particles or bound states that are their own antiparticle), which form, according to recent experiments, in a one-dimensional channel with strong spin-orbit interaction coupled to a superconductor [9]. Another direction to pursue with spectroscopy would be to understand in more detail the creation of entangled spins by splitting a Cooper pair into two different quantum dots coupled to the same superconductor [10]. More intriguing physics may await us as we explore all that impurities have to offer in hybrid superconducting nanosystems [4].

References

J-D. Pillet, P. Joyez, R. Žitko, and M. F. Goffman, “Tunneling spectroscopy of a single quantum dot coupled to a superconductor: From Kondo ridge to Andreev bound states,” Phys. Rev. B 88, 045101 (2013)
S. De Franceschi, L. Kouwenhoven, C. Schönenberger, and W.Wernsdorfer, “Hybrid Superconductor-Quantum-Dot Devices,” Nature Nanotech. 5, 703 (2010)
L. Kouwenhoven and L. Glazman, “Revival of the Kondo effect,” Physics World 14, 33 (2001)
L. I. Glazman and K. A. Matveev, “Resonant Josephson Current through Kondo Impurities in a Tunnel Barrier,” JETP Lett. 49, 659 (1989)
J. Bauer, A. Oguri, and A. C. Hewson, “Spectral Properties of Locally Correlated Electrons in a Bardeen–Cooper–Schrieffer Superconductor,” J. Phys. Condens. Matter 19, 486211 (2007)
M. R. Buitelaar, T. Nussbaumer, and C. Schönenberger, “Quantum Dot in the Kondo Regime Coupled to Superconductors,” Phys. Rev. Lett. 89, 256801 (2002)
J. A. Van Dam, Y. V. Nazarov, E. P. A. Bakkers, S. De Franceschi, and L. P. Kouwenhoven, “Supercurrent Reversal in Quantum Dots,” Nature 442, 667 (2006); R. Maurand, T. Meng, E. Bonet, S. Florens, L. Marty, and W. Wernsdorfer “First-Order 0- $π$ Quantum Phase Transition in the Kondo Regime of a Superconducting Carbon-Nanotube Quantum Dot,” Phys. Rev. X 2, 011009 (2012)
J.-D. Pillet, C. H. L. Quay, P. Morfin, C. Bena, A. Levy Yeyati, and P. Joyez, “Andreev Bound States in Supercurrent-Carrying Carbon Nanotubes Revealed,” Nature Phys. 6, 965 (2010)
L. Fu and C. Kane, “Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator,” Phys. Rev. Lett. 100, 096407 (2008)
L. Hofstetter, S. Csonka, J. Nygård, and C. Schönenberger, “Cooper Pair Splitter Realized in a Two-Quantum-Dot Y-Junction,” Nature 461, 960 (2009)

About the Authors

Romain Maurand is a postdoctoral researcher in the nanoelectronics group of the University of Basel, Switzerland. He obtained his Ph.D. at the Joseph Fourier University working at the CNRS Néel Institute in Grenoble, France. His research focuses on quantum electronic transport in hybrid devices based on single carbon nanotube or graphene.

Christian Schönenberger is a full professor in experimental condensed matter physics at the University of Basel, where he leads the nanoelectronics group. He is also the acting director of the Swiss Nanoscience Institute (SNI) at the University of Basel. A particular focus of his research concerns hybrid quantum devices that are built on novel low-dimensional materials such as carbon nanotubes and graphene, for which the group has a research record since 1998. He is also a recipient of an ERC advanced research grant and a fellow of the American Physical Society.