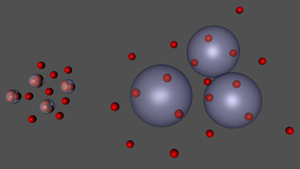
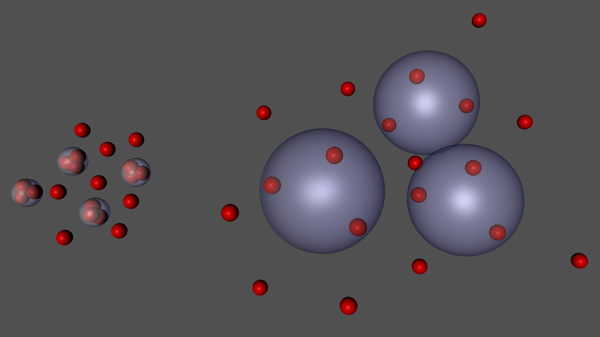
Giant Efimov States Now Observed
The bound states of three identical bosons with resonant pairwise interactions have fascinated physicists since they were proposed by Vitaly Efimov in the 1970s [1]. When such states occur, three particles can form a bound quantum state even if two particles alone cannot form a pair. Like the famed Borromean rings (often used to visualize Efimov states), breaking any one bond would thus destabilize the entire threesome. Theory predicts that the Efimov trimers should follow a discrete geometrical scaling: a copy of the original that is larger by a factor λ∼22.7 will also be stable, and so on to larger and larger sizes (Fig. 1). Observing this property has, however, proven to be extremely difficult. A collaboration between Bo Huang, Leonid A. Sidorenkov, and Rudi Grimm at the University of Innsbruck, Austria, and Jeremy M. Hudson at Durham University, UK, has now met the challenge. In a paper in Physical Review Letters [2], they report the observation of trimers formed by ultracold cesium ( Cs) atoms that are almost 22.7 times larger than the ones they observed previously in the same system [3]. This confirms the theoretical scaling factor and opens up exciting new possibilities for the experimental study of universal few-body phenomena with ultracold atoms.
In quantum mechanics, the interaction between two particles is said to be resonant when the energy of the free particles is very close to the binding energy of the pair. In these conditions, most of the properties of the pair can be described in terms of a single real number, the scattering length a. Efimov showed that when a third identical particle gets close to the previous two, very interesting phenomena arise. First, the interaction is reinforced and can keep the three particles together even when two alone could not. Second, the effective interaction between the three particles is at long range even if the pairwise interaction arises from short range forces. A special property of the long-range potential is that it can support a full series of trimers with properties scaling geometrically with the discrete parameter λ: the size of successive trimers is larger by λ, while their binding energy is smaller by λ2. This phenomenon was predicted to be universal, such that it could be tested on elementary particles, nuclei, atoms, molecules, etc. [1,4,5].
For decades following Efimov’s work, this fundamental state of matter has been elusive. The primary candidates for its observation were nuclear and molecular systems, where the interaction between pairs is rather strong but cannot be easily controlled and enhanced by making it resonant [4,5]. The situation has changed with the advent of ultracold atoms, in which the interaction can be tuned via magnetic fields through the so-called Feshbach resonances [6], a mechanism originally predicted for nuclear systems. In 2006, the same group in Innsbruck reported the formation of an Efimov trimer state in a sample of ultracold Cs atoms [3]. Successive studies have shown that this was indeed the smallest of the possible Efimov trimers.
That first observation triggered an explosion of experimental and theoretical studies on different atomic systems, aiming at verifying the predicted universal properties [7]. Other universal properties of the Efimov trimers have been discovered, but observing the geometrical scaling has proven to be problematic for two main reasons. First, the temperature of the atomic samples must be comparable or smaller than the binding energy of the trimer, otherwise they tend to break as soon as they are formed. While temperatures of the order of 100 nanokelvin are enough for the smallest trimer, one needs, in principle, a temperature lower by a factor λ2(∼515) to observe the next larger one. Second, the size of the trimer scales with the scattering length, so that very large scattering lengths (i.e., strong mutual interactions) are needed to observe the second trimer, a regime in which, at normal densities, atomic ensembles tend to become unstable and fly apart.
The researchers in Innsbruck have now developed an ultraweak trap for their ultracold Cs atoms, which solves both problems. Starting from a standard ultracold sample, they expand it in the new trap to very low temperatures and densities and to sizes large enough to host large Efimov trimers. By varying the strength of the interaction through the controllable Feshbach resonance, they then scan the scattering length around large negative values; they prefer to work with a<0 because, since dimers can only exist at a>0, there is no dimer state that can perturb the measurements [8,9]. When the absolute value of the scattering length gets close the trimers’ size, the binding energy of the trimers becomes equal to the energy of three free atoms, and the Efimov trimers can start to form spontaneously [1,5]. The trimers’ formation is detected as a loss of atoms, since the Efimov trimers are very unstable and can break down into very energetic atoms, which fly away from the trap. By searching this increase of losses, the researchers can measure very precisely the critical scattering length—about 1 micrometer. In the analysis, they take into account the finite temperature of their system, which can lead to a broadening and a shift of the loss peak [10].
This value is 21.0 (with an uncertainty of 6%) times larger than the one they measured for the smaller trimers, which was about 50 nanometers [3]. Within the measurement’s precision, this observation is consistent with Efimov’s prediction of a factor of 22.7.
These results have important consequences. They demonstrate the existence of the second Efimov trimer and verify the scaling factor predicted by the theory. They also show the way to access experimentally the proper regime for the second trimer. It is now important that the universality of this behavior is tested on other atomic systems. At the large scattering lengths reached in the Innsbruck experiment, other features of the Efimov trimers can be explored; for example, their breakup into an atom-plus-dimer combination.
Another important goal would be to further test the scaling itself by measuring the size of three or more successive Efimov trimers. This would require pushing the experiments to a completely new regime, beyond the present capabilities. Another approach would be to study systems where two heavy particles are bound to a lighter one, which leads to a much stronger interaction than for three identical particles. As indicated by Efimov and others [1,11], for large mass difference, λ can be made much smaller than 22.7, and the scaling might be studied with the present technology. Although controlling the temperature in mixtures is harder, recent experiments on lithium-cesium mixtures are indeed starting to observe signatures of three trimer states with increasing sizes [12,13].
References
- V. Efimov, “Energy Levels Arising from Resonant Two-Body Forces in a Three-Body System,” Phys. Lett. B 33, 563 (1970); “Weakly-Bound States of Three Resonantly-Interacting Particles,” Sov. J. Nucl. Phys. 12, 589 (1971); “Few-Body Physics: Giant Trimers True to Scale,” Nature Phys. 5, 533 (2009)
- Bo Huang ((黄博)), Leonid A. Sidorenkov, Rudolf Grimm, and Jeremy M. Hutson, “Observation of the Second Triatomic Resonance in Efimov’s Scenario,” Phys. Rev. Lett. 112, 190401 (2014)
- T. Kraemer et al., “Evidence for Efimov Quantum States in an Ultracold Gas of Caesium Atoms,” Nature 440, 315 (2006)
- E. Nielsen, D. V. Fedorov, A. S. Jensen, and E. Garrido, “The Three-Body Problem with Short-Range Interactions,” Phys. Rep. 347, 373 (2001)
- E. Braaten and H.-W. Hammer, “Universality in Few-Body Systems with Large Scattering Length,” Phys. Rep. 428, 259 (2006)
- C. Chin, R. Grimm, P. Julienne, and E. Tiesinga, “Feshbach Resonances in Ultracold Gases,” Rev. Mod. Phys. 82, 1225 (2010)
- F. Ferlaino and R. Grimm, “Forty Years of Efimov Physics: How a Bizarre Prediction Turned into a Hot Topic,” Physics 3, 9 (2010)
- M. Zaccanti, B. Deissler, C. D’Errico, M. Fattori, M. Jona-Lasinio, S. Müller, G. Roati, M. Inguscio, and G. Modugno, “Observation of an Efimov Spectrum in an Atomic System,” Nature Phys. 5, 586 (2009)
- S. E. Pollack, D. Dries, and R. G. Hulet, “Universality in Three- and Four-Body Bound States of Ultracold Atoms,” Science 326, 1683 (2009)
- B. S. Rem et al., “Lifetime of the Bose Gas with Resonant Interactions,” Phys. Rev. Lett. 110, 163202 (2013)
- J. P. D’Incao and B. D. Esry, “Mass Dependence of Ultracold Three-Body Collision Rates,” Phys. Rev. A 73, 030702 (2006)
- S.-K. Tung, K. Jimenez-Garcia, J. Johansen, C. V. Parker, and C. Chin, “Observation of Geometric Scaling Of Efimov States in a Fermi-Bose Li-Cs Mixture,” arXiv:1402.5943 (2014)
- R. Pires, J. Ulmanis, S. Häfner, M. Repp, A. Arias, E. D. Kuhnle, and M. Weidemüller, “Observation of Efimov Resonances in a Mixture with Extreme Mass Imbalance,” arXiv:1403.7246 (2014)