A New Phase of Solid Oxygen

Susumu Kitagawa

Viewpoint

A New Phase of Solid Oxygen

Institute for Integrated cell-Material Sciences, Kyoto University, Yoshida, Sakyo-ku, 606-8501, Japan

June 16, 2014• Physics 7, 63

A large applied magnetic field can bring solid oxygen into a novel phase—a consequence of the strong spin-lattice coupling in the molecular crystal.

Figure caption — **Figure 1:** (a) Possible geometrical arrangements of the $O_{2}$ - $O_{2}$ dimer [2]: H geometry (parallel), S geometry (canted), or X geometry (crossed). (b) Evidence of a field-induced magnetic phase transition in solid oxygen. While previous studies explored a range of applied fields up to $\sim 50$ T, an abrupt increase in magnetization is observed by Matsuda and co-workers as the field reaches $123$ T [1]. The hysteresis loop suggests a first-order phase transition.

Molecular crystals, like sugar, ice, or solid chalcogens (the elements of group $16$ of the periodic table, such as oxygen) are made of molecules held together by van der Waals forces. As they crystallize, they form structures that depend on the characteristics of the intermolecular interactions. Among various simple molecules, solid molecular oxygen ( $O_{2}$ ) is unique because it carries a magnetic moment with a spin quantum number $S = 1$ . This results in a complex relationship between the magnetic interaction and crystal structure, which has long attracted the attention of scientists—solid oxygen is regarded as a unique example of a spin-controlled system. In Physical Review Letters [1], a team led by Yasuhiro Matsuda at the University of Tokyo, Japan, has reported the discovery of a novel phase of solid $O_{2}$ that can be reached by applying an extraordinarily strong magnetic field [ $120$ – $193$ tesla (T)]. The experiments indicate this is the result of a first-order transition that is both a magnetic and structural transition: the antiferromagnetic phase collapses and the crystal symmetry changes. The finding adds a new dimension to the phase diagram of oxygen and is a key demonstration of how strongly spin and lattice are coupled in the solid.

Molecular crystals exhibit various kinds of interesting structures because of the delicate balance of intermolecular interactions. In the case of ice, the hydrogen bonds determine the low-density structure that is unique among molecular crystals. In dry ice—the solid form of carbon dioxide ( ${CO}_{2}$ )—an electrostatic quadrupole moment causes the characteristic cubic structure (also seen, e.g., in the $α$ phase of solid $N_{2}$ ). The case of solid molecular oxygen is particularly interesting. Faraday discovered the magnetism of $O_{2}$ in 1848, and since then, oxygen has been actively studied as a ubiquitous yet exotic molecular magnet. This magnetism plays an important role via the exchange interaction, leading to fascinating phenomenology in solid phases. At ambient pressure, three different phases ( $α$ , $β$ , and $γ$ ) appear with decreasing temperature. Such phases differ in crystal structure as well as in magnetic properties. The application of pressure induces even more phases: $δ$ [at $5.5$ gigapascal (GPa)], $ε$ ( $8$ GPa), and $ζ$ ( $96$ GPa). The latter is a metallic phase, which even becomes superconducting below $0.6$ kelvin (K). A seventh phase ( $η$ ) has been observed in a high-pressure ( $16$ – $20$ GPa), high-temperature ( $500$ – $1000$ K) range. But despite intense research, it is not yet very well established whether and how the magnetic interaction is essential for the molecular arrangement in the different phases of solid $O_{2}$ .

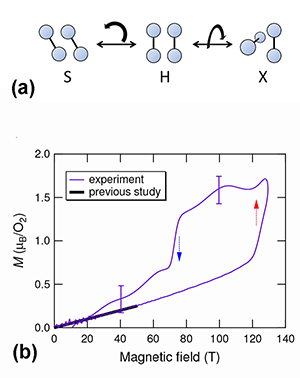
Why can magnetic properties influence structural properties in solid oxygen? First, the exchange interaction (as estimated from experiments) is comparable in strength to the van der Waals forces. Second, the exchange interaction between the magnetic moments of $O_{2}$ , including its sign, depends on the geometry of the molecular arrangement. Ab initio calculations have tackled the simpler case of a $O_{2}$ - $O_{2}$ dimer [2]. They predict that the stable arrangement of the two $O_{2}$ molecules depends on whether the magnetic moments align antiferromagnetically or ferromagnetically. Under normal conditions, an “H geometry” should occur [see Fig. 1(a)]: the two molecules are parallel, the exchange interaction is antiferromagnetic, and the singlet state is favored (that is, the two spins cancel each other, and the total spin is zero). The H geometry is indeed observed in the three phases of solid oxygen. But when the dimer is magnetized, two other geometries are stable: S (canted) and X (crossed) [Fig. 1(a)]. In both, the exchange interaction is ferromagnetic. This leads to the expectation of both magnetic and structural phase transitions resulting from the application of large magnetic fields.

Such theoretical predictions could be tested when, ten years ago, the $O_{2}$ - $O_{2}$ dimer was successfully synthesized by using nanoporous coordination polymers [3]. X-ray diffraction measurements at low temperatures revealed that the H geometry, as in the molecular solid, is robust in the dimer system. However, the magnetic measurements could not be interpreted based on Heisenberg models and H geometry only. To explain the experimental findings, researchers invoked a scenario in which there are excited states of other geometries, e.g., the S or X type [4]. This scenario indicates that a molecular rearrangement may occur in a magnetic field. It was also found that the thermally excited states lead to deviations from the H geometry at higher temperatures. These combined results, obtained on dimers, led to the anticipation of a field-induced structural phase transition in solid $O_{2}$ .

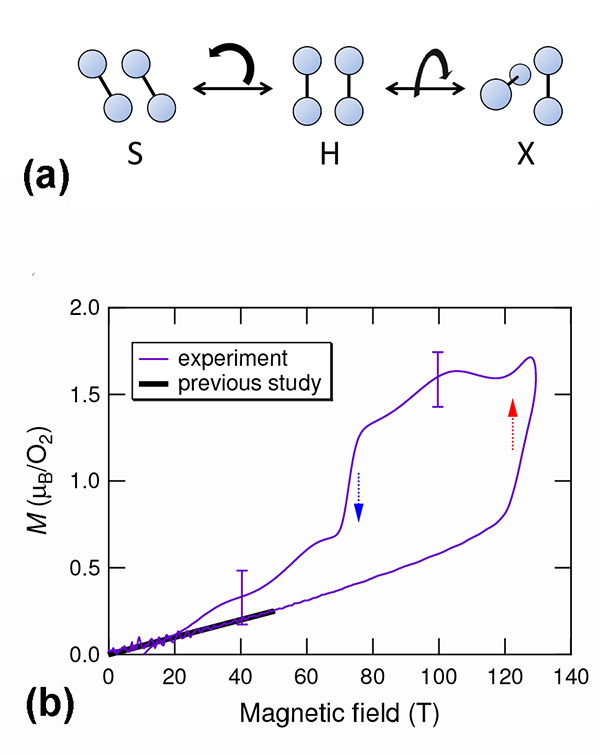
Matsuda’s team explored the possibility of this kind of phase transition starting from the $α$ phase of solid $O_{2}$ , using state-of-the-art techniques for generating microsecond pulses of ultrahigh magnetic fields (of up to $193$ T). Working at low temperatures ( $4.2$ K), they directly measured the magnetization using a pickup coil. Because $α$ oxygen has an antiferromagnetic ground state, the magnetization should linearly increase with increasing magnetic fields. This is true at low magnetic fields. However, a distinct, sudden increase of the magnetization occurs at around $125$ T [see Fig. 1(b)]. This is the clear signature of a magnetic phase transformation. The magnetization curve is also found to have a significant hysteresis between the field-increasing and field-decreasing processes. Hence the phase transition is suggested to be a first-order transition, probably associated with a structural change.

The authors used optical spectroscopy to probe structural changes, measuring transmission changes at visible wavelengths (around $600$ nanometers) as a function of the applied field. The existence of a bimolecular absorption resonance in this wavelength region is well established—it causes the blue color in solid $O_{2}$ . The key effect allowing optical detection of structural changes is the change of light scattering at the domain boundaries in polycrystalline $α$ oxygen. $α$ oxygen is structurally anisotropic (monoclinic). The interface between differently oriented crystal domains, each with anisotropic refractive indices, generates strong scattering, thus making polycrystalline $α$ oxygen opaque for visible light. But if the domains suddenly became isotropic, such scattering would be reduced. What the authors found is that the transmitted light intensity considerably increased at fields where the magnetic transition takes place. The effect is dramatic: The crystal becomes nearly transparent at ultrahigh magnetic fields. Such field-induced transparency clearly demonstrates that the crystal symmetry changes from anisotropic to isotropic. A similar phenomenon has been previously observed in the $β$ -to- $γ$ phase transition, driven by increasing temperature at zero field, in which the crystal structure transforms from the rhombohedral ( $β$ ) to cubic ( $γ$ ).

Magnetization measurements and magnetotransmission optical spectroscopy thus perfectly complement each other, providing compelling evidence of the novel phase of solid $O_{2}$ in ultrahigh magnetic fields. Recalling the magnetic field-induced rearrangement of the $O_{2}$ - $O_{2}$ dimer, the authors attribute the observed structural phase transition to the rearrangement of $O_{2}$ molecules. Dimer results suggest the antiferromagnetic coupling could become unstable in the new molecular arrangement, and ferromagnetic exchange interaction might become favored. This makes the result a noteworthy discovery in the long history of solid $O_{2}$ studies: the eighth phase of solid $O_{2}$ is completely different from the known seven phases at zero field where the exchange interaction between $O_{2}$ molecules is either paramagnetic or antiferromagnetic.

While optical spectroscopy clearly shows a structural transition, an outstanding question is the determination of the crystal structure of the novel phase. This is very challenging since the applied magnetic field is pulsed, with a duration of less than ten microseconds, which makes it difficult to probe the new structure with conventional, static diffraction measurements. In absence of reliable experiments, the puzzle may first be tackled by theoretical predictions of crystal structures. Finally, further studies at higher temperatures will be needed to gather a complete picture of the underlying physics that establishes the entire field-temperature phase diagram of solid oxygen.

References

T. Nomura, Y. H. Matsuda, S. Takeyama, A. Matsuo, K. Kindo, J. L. Her, and T. C. Kobayashi, “Novel Phase of Solid Oxygen Induced by Ultrahigh Magnetic Fields,” Phys. Rev. Lett. 112, 247201 (2014)
B. Bussery and P. E. S. Wormer, “A van der Waals Intermolecular Potential for (O $_{2}$ ) $_{2}$ ,” J. Chem. Phys. 99, 1230 (1993)
R. Kitaura et al., “Formation of a One-Dimensional Array of Oxygen in a Microporous Metal-Organic Solid,” Science 298, 2358 (2002)
A. Hori et al., ”Spin-Dependent Molecular Orientation of O $_{2}$ –O $_{2}$ Dimer Formed in the Nanoporous Coordination Polymer” J. Phys. Soc. Jpn. 82, 084703 (2013)

About the Author

Susumu Kitagawa is the director of the Institute for Integrated Cell-Material Sciences, Kyoto University and professor of functional chemistry, faculty of Engineering, Kyoto University. His research background is in inorganic chemistry, focusing on coordination network materials, which are now known as porous coordination polymers (PCPs) or metal-organic frameworks (MOFs). The focus of his group is to design and synthesize functional porous materials for science and technology of storage, separation, and conversion of gas substances. See more at http://www.sbchem.kyoto-u.ac.jp/kitagawa-lab/index-e.html