Microwave Photons Move Out of Equilibrium

Mohammad Hafezi

Viewpoint

Microwave Photons Move Out of Equilibrium

Mohammad Hafezi

Department of Electrical and Computer Engineering, University of Maryland, College Park, MD 20742, USA

September 8, 2014• Physics 7, 92

A circuit for microwave photons provides a useful test bed for nonequilibrium physics.

Figure caption — **Figure 1:** Raftery *et al.* designed a circuit for microwave photons to study the behavior of interacting quantum objects out of equilibrium. (Top: A schematic; bottom: The actual device.) Photons oscillate back and forth between two resonators (indicated by the yellow cylinders), each of which is coupled to a “transmon.” This coupling makes the device inherently nonlinear: the spacing between the energy levels on the resonators (inset) varies with $g N^{1 / 2}$ , where $N$ is the number of excitations on each site and $g$ is a coupling constant.

Isolated systems that don’t exchange energy with the “outside world” are the easiest to study and control. But most real systems are decidedly not in isolation, nor are they in equilibrium. These include turbulent waves, earthquakes, and the rapidly cooled metal alloys and plastics used in manufacturing. Even richer physics lies in quantum systems that are out of equilibrium, particularly those in which interactions between multiple quantum objects is important. Such systems are difficult to describe theoretically, but investigating them could shed light on fundamental questions about how quantum systems thermalize [1] and the formation of the early Universe. Long term, studying these systems could open new avenues of research in quantum field theory and the quantum simulation of atomic and molecular chemistry.

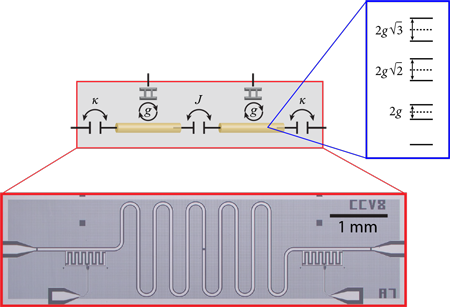
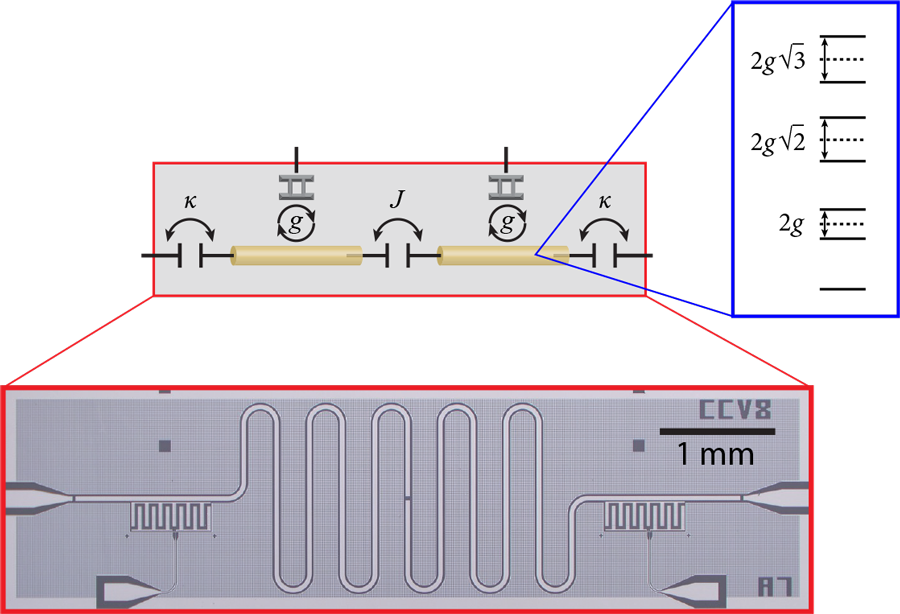
James Raftery and Darius Sadri at Princeton University, New Jersey, and their colleagues now report a model experimental device that provides an early step towards understanding nonequilibrium many-body physics in a quantum system. To this end, they study the time evolution of a small number of microwave photons moving back and forth between two resonators with leaky ports [2]. This elegant experimental device is designed to be simple enough that it can be described with a toy model yet complex enough to include two ingredients of interest in nonequilibrium physics: dissipation and strong photon-photon interactions. The researchers showed they could use this interaction to drive photons in the circuit into a self-trapped state—a demonstration that complements similar observations in cold-atom and photonic devices. Moreover, their device is designed with circuit elements similar to those used in prototype quantum computers, thus the findings could be relevant for future practical applications.

The circuit designed by Raftery et al. consists of two microwave resonators, each coupled to a quantum bit (qubit) called a transmon (Fig. 1). Each qubit contains a superconducting Josephson junction whose inductance has a nonlinear dependence on electrical current. This nonlinear effect mediates a strong interaction between photons: The presence of the qubit changes the energy levels the photons can occupy from those of a harmonic oscillator, with a fixed spacing between levels, to a nonlinear oscillator, in which the level spacing changes as zero, one, two, etc., photons are added to the resonator (Fig. 1, inset). Specifically, the level spacing forms an anharmonic ladder, varying as $g N^{1 / 2}$ , where $N$ is the number of excitations on each site and $g$ is a coupling constant between each resonator and its respective transmon.

The two resonators are connected by a capacitor, which allows photons to transmit from one resonator to the other at a rate $J$ . Experimentally, $g$ and $J$ are fixed by how the circuit is fabricated, so to control the behavior of the device, Raftery et al. vary the number of photons on the resonator. Dissipation—the loss of energy—occurs because photons can leak out of the resonators.

If the photons can’t escape or be absorbed, and if they don’t interact with each other ( $g = 0$ ), the expected behavior of the device is simple: photons oscillate back and forth between the two resonators. In particular, if we start with $N$ photons on one site, the photon population oscillates at a rate proportional to $J$ . The nonlinear effects modify this oscillation, and at a critical value $g_{c} = 2.8 J N^{1 / 2}$ , the period of the oscillation diverges. For larger values of coupling, all of the photons get trapped on one site, and the left/right symmetry is broken.

This “self-trapping” has been observed in several systems. The behavior was predicted in the 1980s for two coupled nonlinear oscillators with quadratic nonlinearity [3,4]. Similar behavior was predicted for ultracold atoms [5]. In particular, experimentalists have shown that two coupled, trapped Bose-Einstein condensates exhibit self-trapping by varying the initial population difference [6]. More recently, similar effects were observed for exciton-polaritons in a semiconductor device [7].

However, there is a major difference between the self-trapping Raftery et al. are able to observe in their device and that observed in the quadratically nonlinear systems. In their device, the energy difference between two consecutive energy levels decreases with $N$ (recall, $E (N + 1) - E (N) = g (N + 1)^{1 / 2} - g N^{1 / 2}$ ), which means that as more photons are added to the device, its behavior becomes more “classical.” This is in contrast to the quadratic nonlinear systems in which the energy spacing increases linearly with the number of excitations. In these systems, the self-trapping occurs for a high number of excitations and classical behavior reappears for a low number of excitations.

In order to probe the self-trapping phenomena, Raftery et al. measure the electric field associated with the photons escaping from the resonators. If the initial number of photons is below the critical number, the photons self-trap on one resonator—consistent with what the researchers predicted in earlier work [8]. But if the initial number of photons is above the critical number, then the light oscillates back and forth between the resonators. Of particular interest is that this photonic system is genuinely dissipative: photons leak out of both sites. Consequently, if the system is initialized with a number of photons greater than the critical number, it slowly decays, and at some point, the total number of photons on the two resonators falls below the critical number, and the system evolves from a delocalized state to a self-trapped state. In other words, the intrinsic dissipation in the system drives a transition from delocalized to self-trapped states, without the need of changing any parameter externally.

Although the presented work can be understood by a semiclassical formalism, it paves the way for further investigations of many-body nonequilibrium physics with microwave photons for which the semiclassical description is no longer valid. In particular, scaling up their device from a dimer to many sites is a realistic approach to study many-body nonequilibrium physics.

More generally, photons, in all frequency domains, provide an intriguing medium to study many-body physics. Photonic systems are naturally open, and therefore their ground state is simply the vacuum. Consequently, photonic systems have to be externally driven, as in the device studied by Raftery et al., which makes the nonequilibrium physics immediately relevant. Of particular interest would be to use the interactions between photons on their device to cause quantum many-body phenomena to emerge: Physicists are still looking for the best ways to prepare many-body states of photons and the best formalisms to describe them. For example, researchers are interested in finding a measurable quantity, such as incompressibility, that contains information about the many-body aspects of a correlated systems. All these questions make the subject of dissipative-driven many-body physics exciting, from both a theoretical and experimental view.

This research is published in Physical Review X.

References

A. Polkovnikov et al., “Nonequilibrium Dynamics of Closed Interacting Quantum Systems,” Rev. Mod. Phys. 83, 863 (2011)
J. Raftery, D. Sadri, S. Schmidt, H. E. Türeci, and A. A. Houck, “Observation of a Dissipation-Induced Classical to Quantum Transition,” Phys. Rev. X 4, 031043 (2014)
J. C. Eilbeck, P. S. Lomdahl, and A. C. Scott, “The Discrete Self-Trapping Equation,” Physica D 16, 318 (1985)
S. M. Jensen, “The Nonlinear Coherent Coupler,” J. Quant. Electron. 18, 1580 (1982)
A. Smerzi, S. Fantoni, S. Giovanazzi, and S. R. Shenoy, “Quantum Coherent Atomic Tunneling between Two Trapped Bose-Einstein Condensates,” Phys. Rev. Lett. 79, 4950 (1997)
M. Albiez, R. Gati, J. Fölling, S. Hunsmann, M. Cristiani, and M. K. Oberthaler, “Direct Observation of Tunneling and Nonlinear Self-Trapping in a Single Bosonic Josephson Junction,” Phys. Rev. Lett. 95, 010402 (2005)
M. Abbarchi et al., “Macroscopic Quantum Self-Trapping and Josephson Oscillations of Exciton Polaritons,” Nature Phys. 9, 275 (2013)
S. Schmidt, D. Gerace, A. A. Houck, G. Blatter, and H. E. Türecin, “Nonequilibrium Delocalization-Localization Transition of Photons in Circuit Quantum Electrodynamics,” Phys. Rev. B. 82, 100507 (2010)

About the Author

Mohammad Hafezi is an Assistant Professor of Electrical and Computer Engineering at the University of Maryland (UMD), and a fellow at the Joint Quantum Institute (NIST-UMD) and IREAP. He received his diploma from Ecole Polytechnique (Palaiseau) in 2003. After obtaining his Ph.D. from the physics department at Harvard University, he moved to the Joint Quantum Institute as a postdoc in 2009. His research is at the interface of theoretical and experimental quantum optics and condensed-matter physics with a focus on fundamental physics and applications in quantum information science, precision measurement, and integrated photonics.