Frequency Comb Produces an Entangled Web

Maria  Chekhova

Viewpoint

Frequency Comb Produces an Entangled Web

Max Planck Institute for the Science of Light, 91058 Erlangen, Germany

February 2, 2015• Physics 8, 10

Researchers characterize the multiple ways of entanglement that exist between different frequency bands in a down-converted frequency comb.

Figure caption — **Figure 1:** Illustrated here are the spectra of a frequency comb (a) and of its down-converted radiation in a cavity (b), with entanglement between some frequency components shown by arrows. In order to characterize this entanglement, researchers split the spectrum (c) into multiple frequency bands of equal energy (shown here is a splitting into four frequency bands).

Entanglement underlies all of quantum information science. It is most familiar as a relation between two parts of a single system, in which the properties of each part—taken separately—are uncertain but at the same time correlated with the properties of the other part. This so-called “bipartite entanglement” is, however, just one way in which a system can be entangled. Much more complicated is the entanglement between multiple parts of a system. Such “multipartite entanglement” is of interest because it is known to improve certain quantum information protocols and enable others, like secret key sharing between multiple parties. However, until recently, no well-established criteria existed for this kind of entanglement, and it is still an open question how a quantum system should be split into parts to provide better resources for quantum computation. Stefan Gerke and his colleagues from the University of Rostock in Germany and their colleagues at the Kastler–Brossel Laboratory in France address this question [1]. They split the spectrum of a down-converted frequency comb into ten parts, or bands, and determined the entanglement between various combinations of these parts. The team utilizes a recently developed measure of entanglement called optimal witnesses. This work provides a recipe for creating multipartite entanglement and opens a perspective for using it in quantum information technologies.

In the most famous example of bipartite entanglement, suggested by Einstein, Podolsky, and Rosen (EPR), two particles have correlated positions and momentums. Measuring the position (momentum) for one particle automatically makes certain the position (momentum) of the other one. The EPR scenario can be realized for light modes as well. In this case, the role of position and momentum is played by field quadratures, which are the real and imaginary parts of the electric field. Two entangled modes can be generated at the output of an optical parametric oscillator (OPO), which, in the simplest case, is a crystal placed in a cavity. If pumped at a single frequency, an OPO produces pairs of down-converted bands that have entangled quadratures, which can be verified by homodyne detection [2].

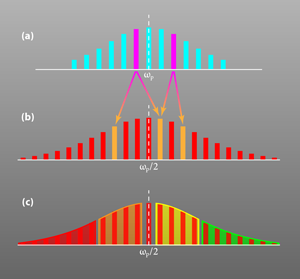
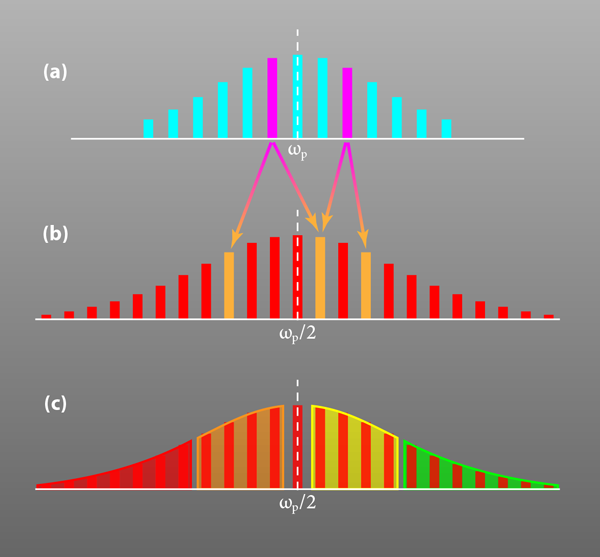
A more complicated form of entanglement occurs when an OPO is pumped by a frequency comb. A frequency comb is a train of coherent (usually femtosecond) pulses, whose broad spectrum (usually several nanometers) consists of narrow lines around a central frequency $ω_{p}$ [Fig. 1(a)]. In the OPO, each spectral line in the original pump beam creates pairs of entangled down-converted bands [Fig. 1(b)]. Taken together, all the down-converted bands overlap to form a broad spectrum centered at $ω_{p} / 2$ , which has been predicted to exhibit multipartite entanglement [3]. The question is how to divide up, or partition, the spectrum so as to recognize and quantify this entanglement.

Bipartite entanglement in a frequency comb has been investigated in detail; for instance, the same Paris group [4] showed that entanglement exists between all 511 possible bipartitions of ten spectral bands selected in the down-converted frequency comb. In other words, regardless of how ten frequency bands were divided into two groups, nonclassical correlations were always obtained between these groups. The researchers characterized the bipartite entanglement using the general approach of finding Schmidt modes [5,6] or supermodes, as they are referred to in Refs. [1] and [4]. The Schmidt modes are chosen in such a way that correlations can be found only between their pairs, the rest of the modes being uncorrelated. This is a natural approach for a simple system like broadband twin beams emitted by a single-frequency pump [5,6], but Schmidt modes are also practical in the more complicated case of a down-converted frequency comb, assuming one is only concerned with bipartite entanglement.

However, in order to investigate the richer multipartite entanglement of a frequency comb, Gerke et al. develop a different strategy [1]. They are not the first to do this, as a recent experiment observed multipartite entanglement in a similar system [7]. But Gerke et al. have now explored the full range of possible entanglements for a given partitioning, allowing them to compare the level of entanglement for different arrangements.

The researchers produced their frequency comb by the second harmonic radiation of a titanium-sapphire laser and down-converted it in an OPO consisting of a bismuth borate crystal placed into a 4-meter ring cavity. They detected the down-converted radiation using a homodyne technique, in which the beam under study is overlapped with a coherent beam (called the local oscillator) on a beam splitter, after which two detectors measure the intensities at the two outputs. The difference of these detectors’ photocurrents is proportional to the quadrature of the radiation under study. It is the noise (variance) of the photocurrent difference that tells one about the quadrature entanglement.

The advantage of homodyne detection is that it selects out only the frequency and spatial modes that are present in the local oscillator. This allowed the authors to address certain frequency bands by spectrally shaping the local oscillator. In separate experiments, the team chose four [Fig. 1(c)], six, or ten bands. Correspondingly, various groups could be made by combining these bands in different ways. As an example, four bands can be made into two groups by combining the first band with the third and the second with the fourth. In total, there are seven different ways to assemble four bands into two groups (i.e., there exist seven possible bipartitions). By contrast, there are 15 ways to form various multiple partitions, starting from a single-party state (all four bands placed in one group) and going up to a four-party state (each band forming a separate group). In the ten band case, the total number of partitions is 115,974.

To test entanglement in a particular partition, the authors used optimal witnesses [8]. The test boils down to measuring an entanglement quantifier ( $L$ ), which depends on the noise measurements made through homodyne detection. If $L$ is below (violates) a certain bound, the state is witnessed to be entangled, and the lower $L$ is relative to the bound, the greater the entanglement. Gerke et al. found that the $L$ values were below the bound for every possible partition, and the degree of violation varied between 4 and 60 standard experimental deviations for different partitions. They found the greatest entanglement for multiple partitions; for instance, the maximal violation for six frequency bands corresponded to six separate parties and was equivalent to 60 standard deviations below the $L$ bound.

It is remarkable that, at least in the down-converted frequency comb studied by the authors, multipartite entanglement turns out to be much more pronounced than bipartite entanglement. In particular, it is more pronounced than the entanglement between the bipartite Schmidt modes. This raises a question of whether there exist Schmidt-like multipartitions that exhibit entanglement only between each other. Such a decomposition would be a unique characterization of multipartite entanglement, which could be compared for different systems. Another important consideration is that the number of parties in the system could be increased further, as the frequency comb contains more than $10^{5}$ separate spectral lines. Numerical simulations show that 100-party entanglement is possible [9]. This gives hope that down-converted frequency combs can be used as scalable systems for quantum computation, requiring less resources than systems based on bipartite entanglement [2–4,9].

This research is published in Physical Review Letters.

References

S. Gerke, J. Sperling, W. Vogel, Y. Cai, J. Roslund, N. Treps, and C. Fabre, “Full Multipartite Entanglement of Frequency-Comb Gaussian States,” Phys. Rev. Lett. 114, 050501 (2015)
S. Braunstein and P. van Loock, “Quantum Information with Continuous Variables,” Rev. Mod. Phys. 77, 513 (2005)
N. C. Menicucci, S. T. Flammia, and O. Pfister, “One-Way Quantum Computing in the Optical Frequency Comb,” Phys. Rev. Lett. 101, 130501 (2008)
J. Roslund, R. Medeiros de Araujo, S. Jiang, C. Fabre, and N. Treps, “Wavelength-Multiplexed Quantum Networks with Ultrafast Frequency Combs,” Nature Photon. 8, 109 (2014)
C. K. Law, I. A. Walmsley, and J. H. Eberly, “Continuous Frequency Entanglement: Effective Finite Hilbert Space and Entropy Control,” Phys. Rev. Lett. 84, 5304 (2000)
W. Wasilewski, A. I. Lvovsky, K. Banaszek, and C. Radzewicz, “Pulsed Squeezed Light: Simultaneous Squeezing Of Multiple Modes,” Phys. Rev. A. 73, 063819 (2006)
N. Chen, N.C. Menicucci, and O. Pfister, “Experimental Realization of Multipartite Entanglement of 60 Modes of a Quantum optical Frequency Comb,” Phys. Rev. Lett. 112, 120505 (2014)
J. Sperling and W. Vogel, “Multipartite Entanglement Witnesses,” Phys. Rev. Lett. 111, 110503 (2013)
R. Medeiros de Araujo, J. Roslund, Y. Cai, G. Ferrini, C. Fabre, and N. Treps, “Full Characterization of a Highly Multimode Entangled State Embedded in an Optical Frequency Comb Using Pulse Shaping,” Phys. Rev. A 89, 053828 (2014)

About the Author

Maria Chekhova is head of the Quantum Radiation group and Single-Photon Technology unit at the Max Planck Institute for the Science of Light in Erlangen, Germany. She is also part-time affiliated with M.V. Lomonosov Moscow State University. Her research is focused on the generation and characterization of nonclassical light, obtained via nonlinear optical effects as well as from nano-emitters. Her main achievements are investigation of the polarization properties of single-mode biphotons, observation of the dispersion spreading of a biphoton, generation of bright squeezed vacuum in polarization-entangled states and witnessing its macroscopic entanglement. She is teaching courses on quantum optics and related subjects at the Lomonosov Moscow State University and the University of Erlangen-Nuremberg.