Are We on the Brink of the Higgs Abyss?
One of the ambitious goals of particle physics is to elucidate the early history of the Universe and predict its distant future. Particle cosmologists examine whether the known laws of particle physics are consistent with the observed cosmological evolution and what future they might imply. Do such laws require some modifications to explain the present Universe? Do they suggest that the Universe is stable, or do they imply it is “metastable,” that is, temporarily stable on cosmological time scales but headed towards an inevitable, if distant, cataclysmic collapse? A new theoretical analysis by Alexander V. Bednyakov at the Joint Institute for Nuclear Research, Dubna, Russia, and co-workers connects these basic questions to the most recent discoveries obtained at the Large Hadron Collider (LHC) [1]. The authors conclude that if the standard model is correct, the measured values of certain quantities, such as the mass of the Higgs boson, imply the Universe is metastable. However, they also show that stability might be more likely than previous studies indicated.
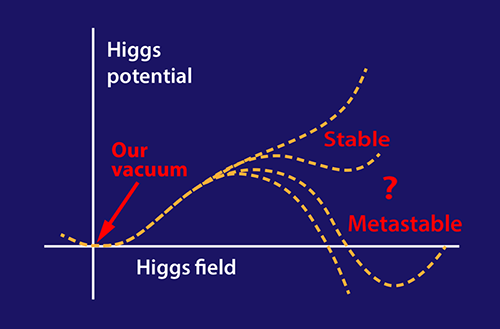
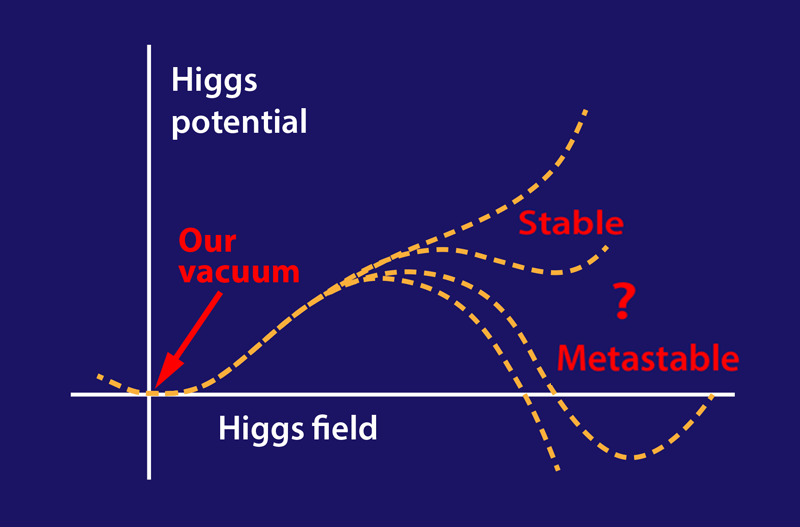
In quantum theory, a stable, “true” vacuum corresponds to the global minimum of the scalar potential, a function that depends on all the scalar fields associated with the fundamental forces of nature. A metastable or “false” vacuum is instead a local minimum. If the Universe lies in the only (or deepest) minimum of the potential, then its future is not threatened. However, it is also possible that the current minimum is “local” and a deeper minimum exists, or the potential has a bottomless abyss separated from the local minimum by a finite barrier. In these cases, the Universe will eventually tunnel out into some other state, in which life as we know it might be impossible. Of course, the probability of such a catastrophic event must be small, because the Universe has remained in its present state for over ten billion years. However, the mere possibility of an inevitable, albeit distant, “end of the world” is disquieting for all.
The discovery of the Higgs boson confirmed that the ground state of the Universe depends on the potential of the Higgs field (see Fig. 1). Whether the Universe is in a true vacuum or a false vacuum can be calculated from the masses of the Higgs boson and the top quark. For such a calculation, one must assume that no physics beyond the standard model, such as new particles or forces, appear up to an extremely high energy scale—the Planck scale. The connection between the masses of these particles and the fate of the Universe is nontrivial. Its analysis is facilitated by a mathematical formalism called “renormalization group evolution” [2], which describes the behavior of a system at different length scales (or, equivalently, energy scales). The renormalization group equations allow researchers to explore the entire shape of the Higgs potential and find any additional maxima and minima.
Questions about the Universe’s stability have been put in sharper focus by the measurements of the Higgs boson’s mass [3]. The current mass estimates, around 125 giga-electron-volts, imply a borderline possibility that the Universe exists in a metastable state [4]. It is of interest, therefore, to refine the theoretical calculations and the associated predictions.
Bednyakov et al. have now carried out a state-of-the-art analysis—arguably the most reliable to date. They calculated the Higgs potential using very precise approximations. For instance, they took into account strong-interactions corrections up to four loops, renormalization group evolution up to three loops, etc. (In the language of Feynman diagrams, a “zero-loop” approximation is the classical description, and higher numbers of loops are needed for more accurate inclusion of quantum effects. However, high-loop orders are notoriously difficult to calculate.)
Their conclusion is that the best theoretical fit to measured parameters, including the Higgs and top-quark masses, points to a metastable Universe. However, their analysis also concludes that values of parameters are closer to a region of absolute stability than suggested by previous studies: it is possible for the Universe to be fully stable (and for the standard model to work all the way up to the Planck scale), if the true values of measured parameters are only 1.3 standard deviations away from the current best estimates. A more precise knowledge of the Higgs boson mass, the top-quark mass, the strong coupling constant, and other parameters will be needed to shed light on the issue.
If the Universe does rest in a false vacuum, one should ask how it got there, despite the presence of a deeper minimum or a bottomless slope in the potential [5]. It has been argued that the formation of negative-energy bubbles prevents the Universe from populating the Higgs false vacuum if deeper minima exist [6]. Therefore, the predicted metastability would imply that the standard model cannot be valid all the way to the Planck scale, and that new particles and interactions must contribute to the scalar potential. If the newly discovered particles are bosons, they will make the scalar potential multidimensional, and one will have to reexamine the Universe’s stability in view of a more complex potential [7].
Another observation one can make is that proximity to instability implies that the Higgs potential is not growing as steeply as one might expect. Scalar fields with shallow potentials tend to develop very large expectation values during inflation in the early Universe. In the case of the Higgs field, its relaxation to the present day minimum can be responsible for the observed matter-antimatter asymmetry [8] (see also 11 February 2015 Synopsis). An understanding of the possible role of the Higgs field in generating the matter-antimatter asymmetry also relies on the knowledge of the Higgs potential at high energy scales.
To understand the future and the past of the Universe, and to assess the validity of eschatological predictions, one now needs more precise measurements of the Higgs boson mass and of other parameters of the standard model. Progress in this direction will come from future experiments at the LHC, as well as at other upcoming facilities, such as the International Linear Collider and the Very Large Hadron Collider. However, the same experiments may also discover new particles and interactions, which would modify the Higgs potential and thus profoundly alter the current discussion on the Universe’s stability.
This research is published in Physical Review Letters.
References
- A. V. Bednyakov, B. A. Kniehl, A. F. Pikelner, and O. L. Veretin, “Stability of the Electroweak Vacuum: Gauge Independence and Advanced Precision,” Phys. Rev. Lett. 115, 201802 (2015).
- Kenneth G. Wilson, “The Renormalization Group: Critical Phenomena and the Kondo Problem,” Rev. Mod. Phys. 47, 773 (1975).
- G. Aad et al. (ATLAS Collaboration), “Observation of a New Particle in the Search for the Standard Model Higgs Boson with the ATLAS Detector at the LHC,” Phys. Lett. B 716, 1 (2012); S. Chatrchyan et al. (CMS Collaboration), “Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC,” 716, 30 (2012); G. Aad et al. (ATLAS Collaboration, CMS Collaboration), “Combined Measurement of the Higgs Boson Mass in pp Collisions at √s=7 and 8 TeV with the ATLAS and CMS Experiments,” Phys. Rev. Lett. 114, 191803 (2015).
- G. Degrassi, S. Di Vita, J. Elias-Miró, J. R. Espinosa, G. F. Giudice, G. Isidori, and A. Strumia, “Higgs Mass and Vacuum Stability in the Standard Model at NNLO,” J. High Energy Phys. 2012, No. 8, 98 (2012).
- M. S. Turner and F. Wilczek, “Is our Vacuum Metastable?,” Nature 298, 633 (1982); A. Kusenko and P. Langacker, “Is the Vacuum Stable?,” Phys. Lett. B 391, 29 (1997).
- J. R. Espinosa, Gian F. Giudice, E. Morgante, A. Riotto, L. Senatore, A. Strumia, and N. Tetradis, “The Cosmological Higgstory of the Vacuum Instability,” J. High Energy Phys. 2015, No. 9, 174 (2015).
- A. Kusenko, P. Langacker, and G. Segrè, “Phase Transitions and Vacuum Tunneling into Charge- and Color-breaking Minima in the MSSM,” Phys. Rev. D 54, 5824 (1996); M. Bobrowski, G. Chalons, W. G. Hollik, and U. Nierste, “Vacuum Stability of the Effective Higgs Potential in the Minimal Supersymmetric Standard Model,” 90, 059901 (2014); J.F. Gunion, H.E. Haber, and M. Sher, “Charge/Color Breaking Minima and A-parameter Bounds in Supersymmetric Models,” Nuclear Physics B 306, 1 (1988).
- A. Kusenko, L. Pearce, and L. Yang, “Postinflationary Higgs Relaxation and the Origin of Matter-Antimatter Asymmetry,” Phys. Rev. Lett. 114, 061302 (2015).