Connecting the Higgs Mass with Cosmic History

Michael Dine

Viewpoint

Connecting the Higgs Mass with Cosmic History

Santa Cruz Institute for Particle Physics and Department of Physics, University of California at Santa Cruz, Santa Cruz, CA 95064, USA

November 23, 2015• Physics 8, 113

A theoretical proposal ties the puzzling light mass of the Higgs particle to a hypothetical new particle that plays an important role during the big bang.

Figure caption — **Figure 1:** Potential of the relaxion field proposed by Graham and colleagues to solve the hierarchy problem. When the relaxion field has a zero value, the Higgs field (not shown) becomes unstable. At this point, the oscillations of the relaxion potential become pronounced.

The mass of the recently discovered Higgs particle is one of the greatest mysteries in present-day particle physics. While much larger than the mass of most known elementary particles, it is far smaller than other energy scales. Within our current understanding of quantum mechanics and relativity, this disparity is puzzling and is referred to as the hierarchy or naturalness problem. One popular explanation is provided by a hypothesized new symmetry of nature, supersymmetry. Peter Graham from Stanford University, California, and collaborators [1] have now put forward an alternative theory in which the hierarchy among mass scales is a consequence of cosmic history. In their theory, the Higgs mass depends on the value of a field dubbed the relaxion. Like the gravitational field, the relaxion pervades all space. Immediately after the big bang, this field repeatedly changes, but at a certain point its value is frozen, and this value is predicted to give a mass to the Higgs comparable to that observed.

More than 40 years ago, Kenneth Wilson [2], who won the physics Nobel Prize in 1982 for his work on understanding questions of energy scales in quantum field theory, formulated the hierarchy problem. He pointed out that the Higgs particle, which is associated with a field (the Higgs field), should naturally have a mass many orders of magnitude larger than the value compatible with other features of the theory. This discrepancy can be described as a failure of dimensional analysis. Particle physicists work under the assumption that physics at particular energy scales is determined by physics at much larger energies. In such a framework, why shouldn’t the Higgs mass be determined by the largest energy scale that one might contemplate? In the standard model of particle physics one finds that there are in fact quantum corrections to the Higgs mass, caused by the coupling of photons and other standard model particles with the Higgs field. These corrections can be extremely large, possibly proportional to the Planck scale [which can be constructed from the gravitational constant and the speed of light and is about $1 0^{19}$ giga-electron-volts $(GeV)$ ] or the scale responsible for the masses of neutrinos (which is believed to be about $1 0^{14} GeV$ ). These scales are far larger than the observed Higgs mass, about $125 GeV$ . Most proposed solutions to this problem postulate the existence of new particles, likely observable at CERN’s Large Hadron Collider, whose coupling to the Higgs field should cancel out the quantum corrections due to standard model particles.

The failure, so far, to observe such new particles has led some theorists to propose anthropic explanations of the Higgs mass. The idea is that the Higgs mass determines the masses of the $W$ and $Z$ bosons, which mediate the weak force that is responsible for the radioactive decay of subatomic particles. Changing the Higgs mass would change the strength of this force, affecting, for example, processes which are crucial to the production in stars of heavy elements such as carbon and iron—the building blocks of life as we know it. If, somehow, nature can select among many possible values of the Higgs mass, for example within a “multiverse” comprising many universes, then, necessarily, observers such as humans find themselves in parts of the Universe where the Higgs mass is such that it allows for the production of heavy elements. But many physicists recoil at this type of explanation, believing that the laws of nature, and the Universe which surrounds us, should be unique.

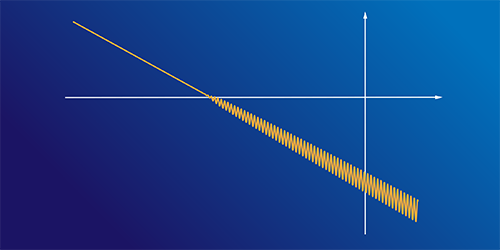
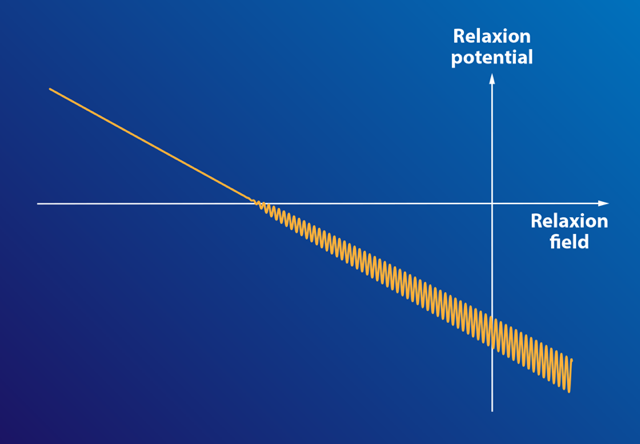
Graham and co-workers propose a very different type of resolution of the hierarchy problem. In their theory, a new field, beyond those already present in the standard model, couples to the Higgs field. This field, the relaxion, can have many different values. More precisely, it has a potential with many local minima (Fig. 1). The Higgs mass depends on the value of this field. At the present time, the relaxion sits in one of these local minima, and the Higgs mass has its observed value. But immediately after the big bang, the relaxion sits far from this point, and the Higgs mass takes a large value compatible with the value expected from dimensional analysis. For this large value, the Higgs field can’t play its assigned role of giving mass to the $W$ and $Z$ bosons. But as the value of the relaxion changes and gives rise to the phenomenon of cosmic inflation, the Higgs mass gradually decreases, eventually becoming zero. Beyond that point, the Higgs field is unstable, and as a result, it takes on a value throughout the Universe. This value is responsible for the masses of the W and Z. In Graham and colleagues’ model, the relaxion tunnels from one minimum to another, but the parameters of the model are such that tunneling automatically stops when the W and Z have their observed values. The Higgs mass is then frozen.

The challenge in this scenario is to find a particle associated with the relaxion that has precisely the required properties. One candidate is a hypothetical particle known as the axion, introduced [3] to solve another puzzle of the standard model: Why do the strong interactions that bind quarks into hadrons, such as protons and neutrons, respect time reversal invariance to an extremely high degree? The axion field has many of the needed properties. Graham and co-workers argue that it can have a potential of the required type (though a recent study [4] raises questions about whether the potential can actually look like that shown in Fig. 1). It turns out that their theory’s association with the axion runs into certain difficulties, but Graham and colleagues suggest alternative candidates for the relaxion that appear promising.

There is another puzzle of the standard model that poses similar challenges. This is the question of the so-called dark energy, which is thought to be causing the Universe to expand at an increasing rate. While dark energy is the dominant form of energy in the Universe at the present time, its density is much smaller than dimensional analysis would predict. It has been proposed that the explanation might be anthropic [5], but an earlier cosmological explanation, invoking a field with features similar to those of the relaxion, was also put forward in the past [6].

This research is published in Physical Review Letters.

References

P. W. Graham, D. E. Kaplan, and S. Rajendran, “Cosmological Relaxation of the Electroweak Scale,” Phys. Rev. Lett. 115, 221801 (2015).
K. G. Wilson, “The Renormalization Group and Strong Interactions,” Phys. Rev. D 3, 1818 (1971).
R. D. Peccei and H. R. Quinn, “CP Conservation in the Presence of Pseudoparticles,” Phys. Rev. Lett. 38, 1440 (1977).
R. S. Gupta, Z. Komargodski, G. Perez, and L. Ubaldi, “Is the Relaxion an Axion?,” arXiv:1509.00047.
S. Weinberg, “The Cosmological Constant Problem,” Rev. Mod. Phys. 61, 1 (1989).
L.F. Abbott, “A Mechanism for Reducing the Value of the Cosmological Constant,” Phys. Lett. B 150, 427 (1985).

About the Author

Michael Dine is Professor of Physics at the University of California, Santa Cruz. In the past, he was a research associate at SLAC, a Long Term Member of the Institute for Advanced Study, and the Henry Semat Professor of Physics at the City College of CUNY. He works on problems in particle physics, astrophysics, and cosmology. A large part of his research effort through the years has been devoted to understanding the hierarchy problem, especially in the context of supersymmetry. He has also done extensive work on axions.