More Power to Atom Interferometry
Atom interferometry, in which atomic waves are coherently split and later recombined, has been called the Swiss Army knife of atomic physics because of its numerous applications [1]. Atom interferometers can be used to study gravity, observe quantum effects, and measure fundamental constants. However, the spitting of atomic beams has always been a challenging task. Several beam splitters for atoms have been developed over the years, many of which rely on complex, high-powered lasers whose photons collide with atoms to steer them along separate beam paths. Paul Hamilton and colleagues at the University of California, Berkeley, have built a more versatile beam splitter by using, for the first time, an optical cavity [2]. Laser pulses bounce back and forth inside the cavity, increasing the effective power in standing waves of light and reducing imperfections in the wave fronts. The light concentration within the cavity allows the use of common low-powered lasers for the initial pulses. The new design may lead to a universal atom interferometer with optical gratings that works with a wide range of atomic species.
Atom interferometry applications fall into three broad areas: inertial sensing, measurements of fundamental constants, and demonstrations of quantum phenomena [3]. For inertial sensing, atom interferometers offer such excellent precision for gravimetry, gravity gradiometry, and rotation sensing that there are now proposals for direct dark matter searches and gravitational wave detection with atom interferometers. For fundamental constants, atom interferometers have been used to measure the fine structure constant [4], the universal gravitational constant [5], and atomic properties such as polarizabilities, van der Waals forces, and tune-out wavelengths [6], in many cases with unprecedented precision. In the quantum phenomena category, atom interferometers have been used to study decoherence, topological phases, and quantum many-body physics.
In order to observe atom interference, it is necessary to split a beam of atoms into two or more paths. Physicists have a lot of experience splitting beams. The first beam splitters for light were developed in the 19th century, making possible the inventions of optical interferometers, such as the Mach-Zehnder and Michelson-Morely interferometers. In the case of light, beam splitters are typically pieces of glass that reflect half of the incoming light, while transmitting the rest. Other forms of beam splitters exist for massive particles.
In the case of electrons, the electrostatic biprism—dating back to 1955—splits an electron beam using the electric field from a charged filament [7]. Neutron interferometers—developed in 1974—harness diffraction from solid crystals, a process that scatters neutrons into a coherent superposition of beams[8]. But none of these beam-splitting techniques work for atoms. Atoms stick to surfaces, they are only weakly affected by electric fields, and they certainly don’t propagate very far in solid crystals. Atoms do, however, interact strongly with light, so the first atom beam splitters that appeared in the late 1980s were based on lasers.
By now, a wide variety of beam splitters have been added to the atom optics toolkit: laser pulses, standing waves of light, nanogratings, and magnets. What these methods have in common is that they coherently manipulate the atomic de Broglie waves that represent the center-of-mass motion of atoms. One of the first and most commonly used techniques involves laser pulses. When counterpropagating pulses with particular light frequencies strike an atom, they stimulate so-called Raman transitions that give a coherent combination of momentum kicks to the atom. However, stimulated Raman transitions usually require elaborate laser systems with significant power.
Alternative atom beam splitting techniques pose problems of their own. Standing waves of light can be arranged to form thick “crystals of light” that cause Bragg diffraction of atom waves, but this requires carefully prepared initial momentum states (ultracold atoms). Nanostructure gratings cause atom diffraction via periodic transmission through nanoscale slits, but the gratings absorb atoms that stick to the material. Better beam splitters for atoms, such as the one built by Hamilton et al., may overcome some of these problems and lead the way towards better atom interferometers.
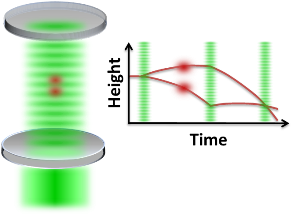
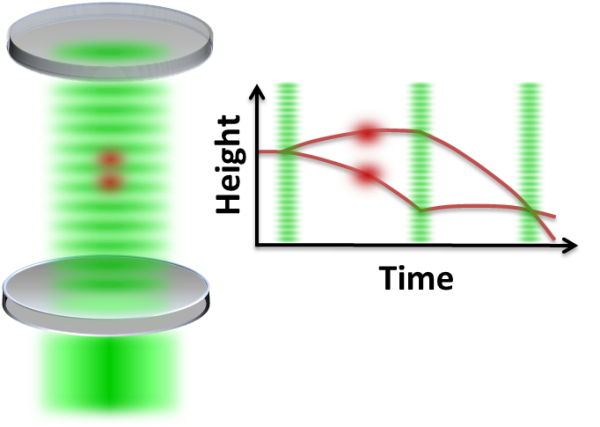
The optical cavity beam splitter works in the same way as previous laser-pulse techniques, but it doesn’t require a high-powered laser. The high-finesse cavity temporarily traps laser light between its curved mirrors, allowing the power to increase by a factor of 150. Hamilton et al. chose the cavity length of 40 centimeters so it would build up power at two distinct wavelengths that together drive stimulated Raman transitions between the hyperfine splitting of the cesium ground state. These transitions induce beam splitting, as the researchers demonstrate in a traditional Mach-Zehnder interferometer. Cesium atoms enter the cavity from one side—their paths curving downward because of the force of gravity (see Fig. 1). A first pulse splits the beam into two by giving half the atoms a kick in the up direction. The second pulse deflects both beams, placing them on a collision path. The third and last pulse combines the beams so that they can interfere. The researchers measured the gravitational acceleration g for the atoms by studying the phase of the atom interference fringes as a function of the time between the laser pulses.
The team demonstrated cesium atom interferometry with just 90 microwatts of input laser light rather than the tens of milliwatts of power needed in previous Raman techniques. Besides the lower power requirement, the cavity design offers several other advantages. The cavity cleans up aberration and speckle from dust and other imperfections. The cavity also suppresses unwanted optical frequencies, helping to create a higher quality beam splitter.
The Berkeley group carried out this experiment with such “finesse” that it inspires us to reflect on other applications for cavity-based atom interferometry. The power buildup cavity may pave the way for a universal atom interferometer that works for all different types of atoms and molecules. Traditionally, atom beam splitters made with standing waves of light need lasers near an atomic resonance, so separate laser systems were required for different atoms. With enhancement by a cavity, it may become possible to use very far off resonant radiation so that the same laser system would work for multiple different types of atoms. Cavity-enhanced atom interferometry may thus improve tests of the weak equivalence principle by enabling measurements of the gravitational free fall for different types of atoms in the same apparatus. Very far off resonant, but powerful enough, standing waves may enable an interferometer for hydrogen, and possibly offer an efficient means to study the gravitational free fall of antihydrogen [9].
This research is published in Physical Review Letters.
References
- E. Callaway, “Extreme Measures: Atom Interferometry’s Precision Could Make it the Swiss Army Knife of Physics,” Science News 173, (2009)
- Paul Hamilton, Matt Jaffe, Justin M. Brown, Lothar Maisenbacher, Brian Estey, and Holger Müller, “Atom Interferometry in an Optical Cavity,” Phys. Rev. Lett. 114, 100405 (2015)
- A. D. Cronin, J. Schmiedmayer, and D. E. Pritchard, “Optics and Interferometry with Atoms and Molecules,” Rev. Mod. Phys. 81, 1051 (2009)
- R. Bouchendira, P. Cladé, S. Guellati-Khélifa, F. Nez, and F. Biraben, “New Determination of the Fine Structure Constant and Test of the Quantum Electrodynamics,” Phys. Rev. Lett. 106, 080801 (2011)
- G. Rosi, F. Sorrentino, L. Cacciapuoti, M. Prevedelli, and G. M. Tino, “Precision Measurement of the Newtonian Gravitational Constant Using Cold Atoms,” Nature 510, 518 (2014)
- W. F. Holmgren, R. Trubko, I. Hromada, and A. D. Cronin, “Measurement of a Wavelength of Light for Which the Energy Shift for an Atom Vanishes,” Phys. Rev. Lett. 109, 243004 (2012)
- G. Mollenstedt and H. Duker, ”Frensnelscher interferenzversuch mit einem biprisma fur elektronenwellen,” Naturwiss. 42, 41 (1955)
- H. Rauch, W. Treimer, and U. Bonse, “Test of a Single Crystal Neutron Interferometer,” Phys. Lett. A 47, 369 (1974)
- P. Hamilton, A. Zhmoginov, F. Robicheaux, J. Fajans, J. S. Wurtele, and H. Müller, “Antimatter Interferometry for Gravity Measurements,” Phys. Rev. Lett. 112, 121102 (2014)