The Quantum Hall Effect Gets More Practical

Ke He

Viewpoint

The Quantum Hall Effect Gets More Practical

State Key Laboratory of Low-Dimensional Quantum Physics, Department of Physics, Tsinghua University, Beijing 100084, China

May 4, 2015• Physics 8, 41

Thin films of magnetic topological insulators can exhibit a nearly ideal quantum Hall effect without requiring an applied magnetic field.

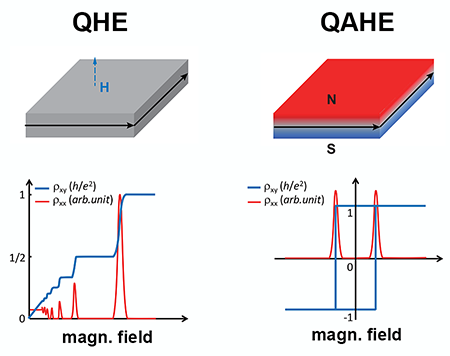
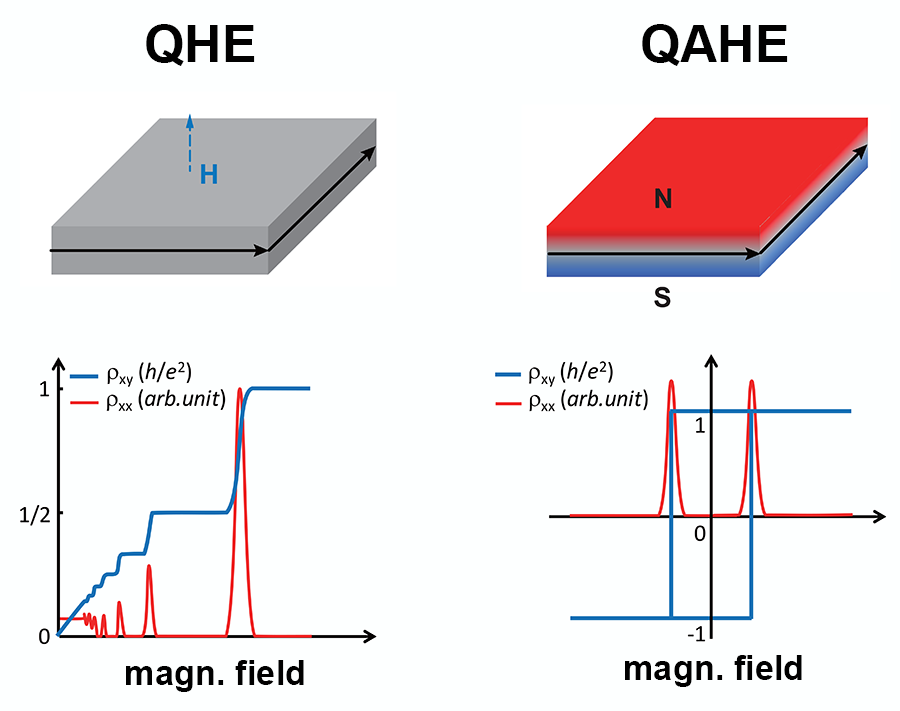
Figure caption — **Figure 1:** (Left) The quantum Hall effect (QHE) occurs in a two-dimensional electron system under a large applied magnetic field. The transverse resistance ( $ρ_{x y}$ ) takes on quantized values while the longitudinal resistance ( $ρ_{x x}$ ) vanishes. (Right) The quantum anomalous Hall effect has quantum Hall features without an applied field. The transverse resistance is precisely quantized at $h / e^{2}$ , where $h$ is Planck’s constant and $e$ the elementary charge, and the longitudinal resistance vanishes at zero field.

The quantum Hall effect is the striking quantization of resistance observed under a large applied magnetic field in two-dimensional electron systems like graphene. In a quantum Hall system, the transverse resistance (measured across the width of the sample) takes on quantized values $h / ν e^{2}$ , where $h$ is Planck’s constant, $e$ the elementary charge, and $ν$ an integer or a fraction. The extreme precision with which the Hall resistance can be measured has important applications in metrology, providing today’s standard definition of the ohm. Another key feature of the effect is that the longitudinal resistance (measured along the length of the sample) vanishes: electrons can be transported without dissipation along the edges of the sample. Quantum Hall systems could thus act as perfect wires with little energy consumption.

From a technological perspective, a dissipationless current is an exciting prospect. But the quantum Hall effect is generally only possible at impractically low temperatures and under strong external magnetic fields. Two independent studies, one by a team led by David Goldhaber-Gordon at Stanford University, California [1], the other by Jagadeesh S. Moodera at the Massachusetts Institute of Technology, Cambridge, and co-workers [2], have now demonstrated that thin films of topological insulators can exhibit a nearly ideal “quantum anomalous Hall effect,” that is, a quantum Hall effect at zero external field [3–5]. The materials feature, in absence of an applied field, a perfect quantization of the transverse resistance and a longitudinal resistance as low as 1 ohm ( $Ω$ ).

Quantum Hall transport can be seen in analogy to atomic physics. In an atom, electrons move around the nucleus without losing their energy, a property guaranteed by the laws of quantum mechanics. A quantum Hall sample is like an atom, but much bigger, allowing electrons to travel a macroscopic distance along the sample edges without energy loss. Such dissipationless quantum Hall edge states result from the unique topological properties of the band structure induced by the magnetic field, which protects electrons from localization or backscattering. The external field required for observing the quantum Hall effect is typically as large as several tesla.

Early theoretical studies [3,4] suggested that a quantum anomalous Hall effect could be possible in materials naturally possessing a topologically nontrivial band structure similar to that induced by the magnetic field (see Fig. 1). The idea, first proposed in 1988 [3], was, however, never implemented until the discovery of topological insulators [6]. In a thin film of a ferromagnetic topological insulator, the combination of spontaneous magnetization and electrons with topological properties could take over the role of an external magnetic field in producing quantum Hall states [4]. In 2013, the quantum anomalous Hall effect was first experimentally observed in thin films of Cr-doped $(Bi,Sb)_{2} {Te}_{3}$ topological insulator [5]. But the longitudinal resistance at zero field was of the order of several k $Ω$ , suggesting that dissipative channels other than the quantum Hall edge states provided a significant contribution to conduction. The resistance only dropped to zero in an applied magnetic field of several tesla, no weaker than that needed for the usual quantum Hall effect [5].

Two mechanisms are likely to contribute to the residual longitudinal resistance of a quantum anomalous Hall sample. First, if the ferromagnetism is not uniform, small regions with different or weaker magnetization can scatter edge electrons into dissipative channels such as surface and bulk states. Second, the dissipative conduction channels can independently carry part of the electrical current. Loosely speaking, the first mechanism adds a resistance in series to the edge-state resistance, while the second creates a parallel resistive channel. This suggests two possible approaches to reduce the zero-field dissipation.

The first approach is to use materials with better ferromagnetic order. This is the approach followed by Moodera’s team. The authors used a magnetic topological insulator material, V-doped $(Bi,Sb)_{2} {Te}_{3}$ , which has an exceptionally large coercivity (the field that reverses the magnetization of a ferromagnetic material): $\sim 1$ tesla at 25 millikelvin [2]. With such a large coercivity, the film at zero field is in a highly ordered ferromagnetic state. This eliminates the regions of weak and heterogeneous ferromagnetism that deteriorate the quantum Hall edge states. The robust ferromagnetism of V-doped $(Bi,Sb)_{2} {Te}_{3}$ allowed the authors to achieve a longitudinal resistance of only about $3 Ω$ as well as a quantization of the transverse resistance to within 6 parts in 10,000.

The second approach is based on minimizing the impact of parallel dissipative electron channels by localizing them. Dissipative channels are thus made to behave like a very large resistance in parallel to the very small resistance of the edge states. The overall sample resistance would thus be dominated by the low resistance. This is the strategy followed by Goldhaber-Gordon’s group, using Cr-doped $(Bi,Sb)_{2} {Te}_{3}$ films. These samples show a very different magnetic field dependence of resistance compared to previous work [5], with the longitudinal resistance dropping to about $15 Ω$ at zero field. The authors further reduce the resistance to around $1 Ω$ by exploiting the cooling effect induced by demagnetization, and they obtain a precise quantization in transverse resistance within 1 part in 10,000. The motion of electrons in a two-dimensional system can be frozen or promoted by quantum interference between different scattering paths, leading to localization or antilocalization, respectively. In a magnetic topological insulator film such as the one used by the authors, the degree of disorder, doping level, and the magnetic properties will control the crossover between different localization or antilocalization regimes [7], each exhibiting a different magnetic field dependence of the longitudinal resistance. Bestwick et al.’s films are evidently tuned to a regime where dissipative electrons are frozen at zero field, but further studies are needed to clarify the exact localization mechanism at play.

The extremely low longitudinal resistance demonstrated in the two experiments indicates that the dissipationless edge states dominate the transport properties at zero magnetic field. Importantly, the effect provides a chance to study the interplay between the quantum Hall effect and other effects that cannot withstand a strong magnetic field, like superconductivity. A superconducting quantum Hall system is predicted to be a chiral topological superconductor [8], which can be used to realize topological quantum computing—a quantum computing approach that is naturally robust against quantum decoherence. But the large field needed for the quantum Hall effect would destroy most superconducting states. The zero-field quantum anomalous Hall effect now opens the door for such studies.

The results are a big step forward towards practical applications of dissipationless quantum Hall edge states. Physicists now need to figure out how to raise the temperature needed to enter the quantum anomalous Hall effect regime, which no study has, so far, been able to increase above 100 millikelvin.

This research is published in Physical Review Letters and Nature Materials.

References

A. J. Bestwick, E. J. Fox, Xufeng Kou, Lei Pan, Kang L. Wang, and D. Goldhaber-Gordon, “Precise Quantization of the Anomalous Hall Effect near Zero Magnetic Field,” Phys. Rev. Lett. 114, 187201 (2015)
C. -Z. Chang et al., “High-Precision Realization of Robust Quantum Anomalous Hall State in a Hard Ferromagnetic Topological Insulator,” Nature Mater. 14, 473 (2015)
F. D. M. Haldane, “Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”,” Phys Rev Lett. 61, 2015 (1988); M. Onoda and N. Nagaosa, “Quantized Anomalous Hall Effect in Two-Dimensional Ferromagnets: Quantum Hall Effect in Metals,” Phys. Rev. Lett. 90, 206601 (2003)
X. -L. Qi, Y. -S. Wu, and S. C. Zhang, “Topological Quantization of the Spin Hall Effect in Two-Dimensional Paramagnetic Semiconductors,” Phys. Rev. B 74, 085308 (2006)
C. -Z. Chang et al., “Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator,” Science 340, 167 (2013)
M. Z. Hasan and C. L. Kane, “Topological Insulators,” Rev. Mod. Phys. 82, 3045 (2010); X. -L. Qi and S. -C. Zhang, “Topological Insulators and Superconductors,” 83, 1057 (2011)
H. -Z. Lu, S. Shi, and S. -Q. Shen, “Competition between Weak Localization and Antilocalization in Topological Surface States,” Phys Rev Lett. 107, 076801 (2011); M. Liu et al., “Crossover between Weak Antilocalization and Weak Localization in a Magnetically Doped Topological Insulator,” 108, 036805 (2011)
X. -L. Qi, Taylor L. Hughes, and S. -C. Zhang, “Chiral Topological Superconductor from the Quantum Hall State,” Phys Rev B 82, 184516 (2010)

About the Author

Ke He is an associate professor of Department of Physics, Tsinghua University, China. He received his Ph.D. in physics from the Institute of Physics, Chinese Academy of Sciences and has worked at the Department of Physics and Institute for Solid State Physics of the University of Tokyo in Japan. His current research focuses on topological-insulator-related materials and quantum phenomena.