Electrons Travel Between Loosely Bound Layers

Kamran Behnia

Viewpoint

Electrons Travel Between Loosely Bound Layers

Laboratoire de Physique et d’Etude de Matériaux Ecole Supérieure de Physique et de Chimie Industrielles, 75005 Paris, France

July 22, 2015• Physics 8, 71

Tungsten-ditelluride cleaves easily into atomically thin layers, but its electrons conduct almost isotropically, suggesting a rare case of good charge conduction across weak mechanical bonds.

Figure caption — **Figure 1:** At left, an electron (green) in ${WTe}_{2}$ travels a long distance between two scattering events (yellow). In the presence of a magnetic field (center and right) the electron experiences a Lorentz force, which bends its trajectory and makes its apparent resistance higher. The magnitude of the effect scales as the square of the magnetic field strength B, provided the mobility, $𝜇$ , of the electron stays constant with field. But in most materials, charge mobility does not remain constant in a magnetic field, and the signal does not grow as fast as B-squared. ${WTe}_{2}$ , in contrast to other semimetals, keeps the same mobility from zero field to a strong field and has a large magnetoresistance at all fields. (Note that in the CGS and MKS system of units, $B 𝜇$ is a dimensionless number.)

In materials science, the quest to solve one mystery can lead to the discovery of another puzzle. That’s the case with the material tungsten-ditelluride ${WTe}_{2}$ , a layered compound that researchers have been actively studying in the last year to understand its unusual magnetoresistance—a property of interest for designing magnetic hard drives and sensors. As reported by Wai-Kwong Kwok at Argonne National Laboratory, Illinois, and colleagues, this material, which was thought to be a two-dimensional metal because of the ease with which it can be cleaved into single atomic layers, has an electronic structure surprisingly close to that of a three-dimensional metal. It remains to be seen whether this finding, which is consistent with that of an earlier measurement, will tell us the origin of ${WTe}_{2}$ ’s magnetoresistance. But the result is interesting in its own right because it shows that the mechanical and electrical properties of a material are not always as closely linked as we may assume.

${WTe}_{2}$ is in the class of materials called transition-metal dichalcogenides (TMDs). These materials consist of layers of metal atoms (such as tungsten, W), sandwiched between two layers of chalcogen atoms (such as tellurium, Te). Because of their layered structure, TMDs are easily cleaved. This process can be repeated until one is left with a single atomic layer, a method first used to produce graphene from graphite. TMDs have therefore been considered as quasi-two-dimensional solids. And because they are semiconductors that can be prepared in very thin layers, they are of interest for making nanoscale transistors and other electronics.

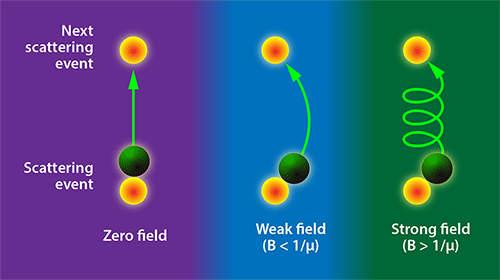
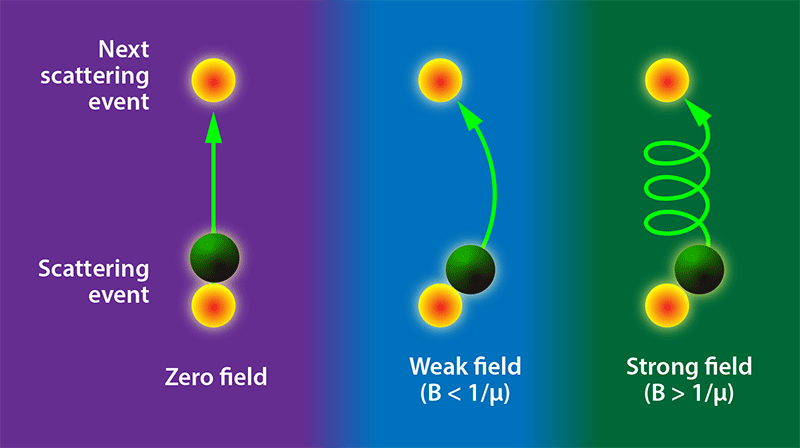
${WTe}_{2}$ in particular has received attention because of the discovery in 2014 that it has a large “unsaturated” magnetoresistance: its resistance steadily increases up to 60 tesla (T), the highest field at which this material has been tested [2]. Magnetoresistance in this material isn’t completely unexpected. Charged particles that acquire a velocity in an electric field will, in the presence of a magnetic field, experience a Lorentz force. This force curves an electron’s trajectory between two scattering events (Fig. 1), reducing its effective velocity. As a result, the resistance of the material increases, an effect dubbed orbital magnetoresistance. The magnitude of this effect scales with the electrons’ mobility, which, in simple terms, is the ease with which the charges move in an electric field. As a consequence, semimetals such as ${WTe}_{2}$ , bismuth, and graphite, which host a small concentration of very mobile carriers, display a large orbital magnetoresistance.

What makes ${WTe}_{2}$ stand out is that its magnetoresistance increases approximately proportional to the square of the magnetic field strength, B [2]. According to textbooks [3], this is the field dependence that would be observed in a “compensated semimetal”—a metal with an equal number of mobile electrons and holes. But all other known semimetals, including bismuth and graphite fail to follow the “B-squared” rule. Researchers have therefore been wondering what makes ${WTe}_{2}$ such a well-behaved semimetal.

One feature that has received significant attention is that perfect compensation between electron and hole concentration can lead to B-squared dependence. However, compensation is only a necessary condition for this field dependence, not a sufficient one. Rather, in deriving a B-squared magnetoresistance from perfect compensation, one implicitly assumes that the mobility of carriers stays constant (see Fig. 1). Pure bismuth provides a good example. This material has an even number of electrons in each elementary cell of its crystal structure, and as such, is perfectly compensated. But its magnetoresistance does not vary as B-squared because its carrier mobility changes in a magnetic field [4]. In contrast, the mobility of charge carriers in ${WTe}_{2}$ appears to be insensitive to a magnetic field as strong as 60 T [2].

To figure out why, researchers have studied the structure of the Fermi surface of ${WTe}_{2}$ using two experimental probes: angle-resolved photoemission spectroscopy [5, 6], which measures electron momentum at different energies and quantum oscillations of resistivity in a steadily rising magnetic field [7], whose frequency quantifies the cross section of the Fermi surface perpendicular to the direction of the field. These experiments have found a number of interesting features in WTe's Fermi surface, but one observation, based on quantum oscillation measurements, is particularly relevant to the findings by Kwok’s group [1]. When the magnetic field is applied perpendicular to the layers, such that the field affects electrons traveling within individual ${WTe}_{2}$ layers, quantum oscillations appear as expected [7]: They have a frequency that is proportional to the in-plane cross section of the Fermi surface. The more surprising finding is that quantum oscillations also occur when the magnetic field is oriented parallel to the layers. This implies that electrons can also travel coherently when they cross from one layer to the next. Moreover, the out-of-plane frequency is only 3 times larger than the in-plane frequency. Since this frequency is a measure of the Fermi velocity, this tells us the Fermi velocity in ${WTe}_{2}$ is fairly isotropic [7].

Kwok and his colleagues’ experiments support this picture. They measure the angular dependence of the magnetoresistance [1]: They rotate the magnetic field, keeping it perpendicular to the applied electric field but modifying its angle with respect to the ${WTe}_{2}$ layers. They find their data are consistent with a finite ratio between in-plane and out-of-plane transverse magnetoresistance. Using this approach, they quantify the anisotropy of the magnetoresistance, showing it increases with decreasing temperature from 100 K down to 2 K but remains moderate, in fair agreement with the small anisotropies measured with quantum oscillations [7].

Because TMDs cleave easily, researchers believe the layers are held together by weak van-der-Waals interactions. But the facility with which electrons flow across layers in ${WTe}_{2}$ indicates that some electron sharing occurs between adjacent layers. The specific crystal structure of ${WTe}_{2}$ may be relevant: the structure is so distorted [5, 8]that the honeycomb lattice common to most TMDs is barely recognizable. Instead, the metal atoms form zigzag chains, which are understood to behave as one-dimensional conductors [2]. Evidently, these distortions improve the out-of-plane conduction and this leads to a mostly three-dimensional metal.

How can this conduction occur despite the large separation between two W atoms across two Te layers? W atoms reside inside distorted ${WTe}_{6}$ octahedra and the W-Te bonds are ionic, so one possibility is that the off-center position of W atoms makes each polyhedron polar and paves the way for electron sharing across the layers. This sharing is, however, too minimal to significantly influence bonding between layers because there are very few mobile electrons and holes (less than 0.005 per formula unit [7]). Further research will tell us if ${WTe}_{2}$ ’s intriguing three-dimensional conductivity [1, 7]and robust magnetoresistance [2]are intimately related or just accidental fellow travelers.

This research is published in Physical Review Letters

References

L. R. Thoutam et al., “Temperature dependent three-dimensional anisotropy of the magnetoresistance in ${WTe}_{2}$ ,” Phys. Rev. Lett. 115, 046602 (2015).
M. N. Ali et al., “Large, Non-Saturating Magnetoresistance in ${WTe}_{2}$ ,” Nature 514, 205 (2014).
A. B. Pippard, Magnetoresistance in Metals (Cambridge University Press, Cambridge, 1989)[Amazon][WorldCat].
A. Collaudin et al., “Angle Dependence of the Orbital Magnetoresistance in Bismuth,” Phys. Rev. X 5, 021022 (2015).
J. Augustin et al., “Electronic band structure of the layered compound ${Td-WTe}_{2}$ ,” Phys. Rev. B 62, 10812 (2000).
I. Pletikosić et al., “Electronic Structure Basis for the Extraordinary Magnetoresistance in ${WTe}_{2}$ ,” Phys. Rev. Lett. 113, 216601 (2014).
Z. Zhu et al., “Quantum Oscillations, Thermoelectric Coefficients, and the Fermi Surface of Semimetallic ${WTe}_{2}$ ,” Phys. Rev. Lett. 114, 176601 (2015).
B. E. Brown, “The Crystal Structures of ${WTe}_{2}$ and High-Temperature ${MoTe}_{2}$ ,” Acta Cryst. 20, 268 (1966).

About the Author

Kamran Behnia obtained his Ph.D. working on heavy-fermion systems in Grenoble. He then spent two years as a postdoctoral fellow at the University of Geneva. In 1992, he was hired by the National Center for Scientific Research (CNRS) and spent seven years working on organic and cuprate superconductors at Paris-Sud University. Since 2000, he has been based at the École Supérieure de Physique et de Chimie Industrielles (ESPCI) in Paris. He is interested in collective quantum phenomena in a variety of solids ranging from semimetals to superconductors. He is the author of the book Fundamentals of Thermoelectricity (Oxford University Press, 2015).