Where the Weyl Things Are

Ashvin Vishwanath

Viewpoint

Where the Weyl Things Are

Physics Department, University of California, Berkeley, CA 94720, USA

September 8, 2015• Physics 8, 84

Analogs to massless fermions predicted by particle physicists 80 years ago have been found in a crystalline metal and in a photonic crystal.

Figure caption — **Figure 1:** Two possible Fermi surfaces (blue lines) for momentum states on the outer face of a material. (The Fermi surface in two dimensions is a line.) The closed Fermi circle at left represents the usual situation, while the open Fermi arc at right only appears in the context of a Weyl semimetal. The two can be distinguished by counting the number of crossings with an arbitrary closed loop (red). An odd number of crossings can only occur from the Fermi arc. This method was utilized for example in Ref. [3] to identify a Weyl semimetal.

In 1929, the mathematician Hermann Weyl proposed a simplified version of the Dirac equation for relativistic particles, whose solution predicted massless fermions with a definite handedness (or chirality) [1]. Weyl’s equation was intended as a model of elementary particles, but in nearly 80 years, no candidate Weyl fermions have ever been observed in high-energy experiments. Now, analogs of the particles have been discovered in the completely different setting of solids, as reported by three independent research groups. Two teams, one led by Zahid Hasan of Princeton University, New Jersey [2], and the other by Hong Ding of the Chinese Academy of Sciences in Beijing [3], have shown that electron excitations in the semimetal tantalum arsenide (TaAs) behave like Weyl fermions. In a concurrent paper, Marin Soljačić of the Massachusetts Institute of Technology, Cambridge, and his colleagues have observed Weyl-like states in a photonic crystal [4]. Weyl particles are associated with a number of unexpected phenomena, and the authors’ findings may lead to applications in optics or electronics.

When Weyl’s equation reappeared in 1937, it was in a rather different context. While studying the properties of the electronic energy bands of solids, physicist Conyers Herring [5] posed the question: Under what conditions will bands have the same energy? Such degeneracies arise in solids with a high crystal symmetry. But they could, he argued, also occur by accident, with two bands touching at points (or nodes). Near these points, the bands—and the low-energy excitations, or quasiparticles, that can fill them—can be described by an equation that, in the simplest scenario, is essentially identical to the Weyl equation. As a result, these touching points are referred to as Weyl points and the quasiparticles near them are reminiscent of Weyl fermions.

Solid-state theorists have, for several decades, steadily explored the relevance of Weyl points to solids. A prescient paper [6] from the early 1980s suggested that exotic effects, like the chiral anomaly—in which the combination of an applied electric field and a magnetic field generates an excess of particles with a particular chirality—were associated with Weyl fermions and could be observable in solids. A further correspondence has been established more recently with the increased understanding of materials with band structures that are “topologically” protected. In these solids, the electrons’ quantum-mechanical wave functions acquire a phase, as though they were moving in a fictional magnetic field that is defined in momentum space. In contrast to a physical magnetic field, this fictional field (known as a Berry curvature) admits excitations that behave like magnetic monopoles. These excitations are topological defects in the Berry curvature and turn out to be the same thing as the Weyl nodes. Thus, two intriguing objects, chiral fermions and magnetic monopoles, are found to be related depending on whether one describes the system in real space or in momentum space.

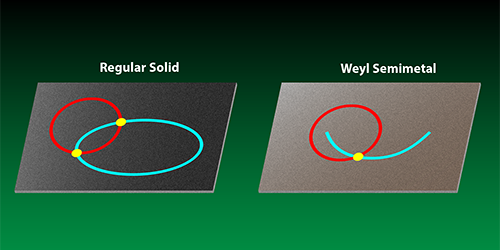
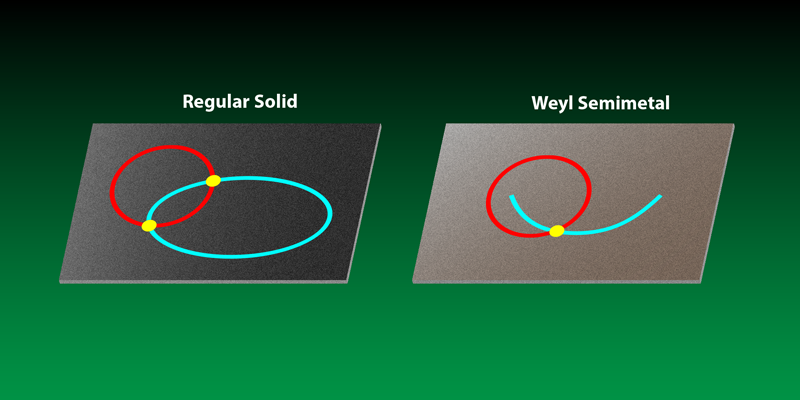
The fact that Weyl nodes are related to magnetic monopoles suggests they will be found in materials that have a topological side to them. In materials known as topological insulators [7] the simplest manifestation of band topology is exotic surface states. The same is true for crystals known as Weyl semimetals, which are associated with very unusual surface states [8]. The surface of a conventional solid has a Fermi surface that forms a closed loop in momentum space; in a Weyl semimetal, these loops become “arcs.” The Fermi arcs terminate at the location of the bulk Weyl points.

Progress in identifying real materials with such surface states has, however, lagged behind theory. One constraint is the energy of the Weyl nodes, which should, ideally, be at or near the Fermi energy. Another is that topological properties associated with a Weyl semimetal only exist in materials that lack either time-reversal symmetry or inversion symmetry. A few years ago, theorists argued that Weyl semimetals should occur in proximity to topological insulators in which inversion symmetry was broken [9]. Building on these ideas, researchers, including the Princeton group, used ab initio calculations to predict candidate materials [10, 11], one of which is TaAs, the material studied by both the Princeton and Chinese Academy of Sciences groups.

In their experiments, Hasan and colleagues and Ding and colleagues used angle-resolved photoemission spectroscopy (ARPES) to detect the Fermi arcs, characteristic of Weyl nodes, on the surface of TaAs. ARPES is an ideal tool for such a purpose. The technique involves shining light on a surface and measuring the energy and momentum of ejected electrons. This allows for the explicit determination of both bulk nodes and the Fermi-arc surface states. Ding’s team used an interesting strategy to identify a Fermi arc and distinguish it from a more conventional closed Fermi surface (Fig. 1). They defined a closed contour in the momentum space spanned by their measurements and investigated how many times surface states at the Fermi energy crossed this contour. Such a contour will intersect a regular Fermi surface an even number of times. But it will intersect a Fermi arc an odd number of times if the arc encloses the projection of a Weyl point, thus providing a clean signature.

Soljačić and his colleagues [4] took a rather different approach to realizing Weyl nodes. Instead of electrons moving through a periodic crystal, they utilized light moving through a photonic crystal—a material with a periodic pattern of holes that only transmits light with certain frequencies. Using a computer-controlled milling machine, the authors carved a precise array of holes into several ceramic layers, which they stacked together to make a 3D photonic crystal with broken inversion symmetry. This structure hosts the electromagnetic-wave analog of Weyl points, which can be accessed by precisely tuning the frequency of a microwave source to the point where the Weyl node occurs.

These experiments finally bring the Weyl equation into the experimental realm. Yet much remains to be done. In TaAs, all manifestations of Weyl physics occur in a narrow window of energies. This requires careful preparation of the material to ensure the Fermi level also lies within this energy window. Candidate Weyl semimetals with larger characteristic energy scales would loosen the constraints on crystal growth. In addition, finding Weyl semimetals that emerge from time-reversal breaking would allow researchers to explore a state with properties analogous to the quantum Hall effect.

Often, new properties lead to new functionalities and applications. Anomalous transport properties that are associated with Weyl physics, such as a reduction of the electrical resistance in the presence of an applied magnetic field, are already being investigated [12]. In optical Weyl systems [4], the number of optical modes has an unusual scaling with the volume of the photonic crystal, which may allow for the construction of large-volume single-mode lasers. Should such effects and applications be realized, they would be a remarkable conclusion to the quest for a simple and beautiful equation that first began eight decades ago.

This research is published in Physical Review X and Science.

References

H. Weyl, “Elektron und Gravitation. I,” Z. Phys. 56, 330 (1929); The Hamiltonian Weyl used to describe particles can be written as $H_{\pm} = \pm c (\begin{matrix} p_{z} & p_{x} - i p_{y} \\ p_{x} + i p_{y} & - p_{z} \end{matrix})$ .
S.-Y. Xu et al., “Discovery of a Weyl Fermion Semimetal and Topological Fermi Arcs,” Science 349, 613 (2015).
B. Q. Lv et al., “Experimental Discovery of Weyl Semimetal TaAs,” Phys. Rev. X 5, 031013 (2015).
L. Lu, Z. Wang, D. Ye, L. Ran, L. Fu, J. D. Joannopoulos, and M. Soljačić, “Experimental Observation of Weyl Points,” Science 349, No. 6248, 622-624 (2015).
C. Herring, “Accidental Degeneracy in the Energy Bands of Crystals,” Phys. Rev. 52, 365-373 (1937).
H. B. Nielsen and M. Ninomiya, “The Adler-Bell-Jackiw Anomaly and Weyl Fermions in a Crystal,” Phys. Lett. B 130, 389 (1983).
J. E. Moore, “The Birth of Topological Insulators,” Nature 464, 194 (2010).
X. Wan, A. M. Turner, A. Vishwanath, and S. Y. Savrasov, “Topological Semimetal and Fermi-Arc Surface States in the Electronic Structure of Pyrochlore Iridates,” Phys. Rev. B 83, 205101 (2011).
S. Murakami, “Phase Transition Between the Quantum Spin Hall and Insulator Phases in 3D: Emergence of a Topological Gapless Phase,” New J. Phys. 9, 356 (2007).
S.-M. Huang et al., “A Weyl Fermion Semimetal with Surface Fermi Arcs in the Transition Metal Monopnictide TaAs Class,” Nature Commun. 6, 7373 (2015).
H. Weng, C. Fang, Z. Fang, B. Andrei Bernevig, and X. Dai, “Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides,” Phys. Rev. X 5, 011029 (2015).
A. A. Burkov, “Chiral Anomaly and Transport in Weyl Metals,” J. Phys. Condens. Matter 27, 113201 (2015).

About the Author

Ashvin Vishwanath is a theoretical physicist specializing in condensed-matter physics. He holds an undergraduate degree from the Indian Institute of Technology, Kanpur, and a Ph.D. from Princeton University. Following a Pappalardo Postdoctoral Fellowship at the Massachusetts Institute of Technology, he joined the University of California, Berkeley, where he is now Professor of Physics. His research interests include the theory of topological phases such as Weyl semimetals, quantum phase transitions, magnetism, and superconductivity. His work has been recognized with a Guggenheim Fellowship (2014) and a Simons Investigator award (2015). He is a Fellow of the American Physical Society and holds a Distinguished Visiting Research Chair at the Perimeter Institute.