Wiring Up Superconducting Qubits
Despite remarkable progress over the past few decades, it remains unclear what form quantum computers will eventually take. Different kinds of quantum bits, or qubits, exist today, but the ideal qubit has yet to emerge. The challenge is that a qubit must satisfy contradictory requirements: It must be isolated from its environment to preserve quantum coherence, but also retain enough coupling to the outside world to enable manipulation and measurement. One possible solution is to combine the advantages of several types of qubits in hybrid architectures.
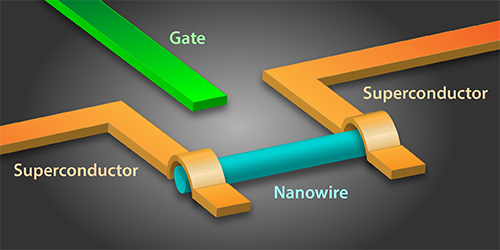
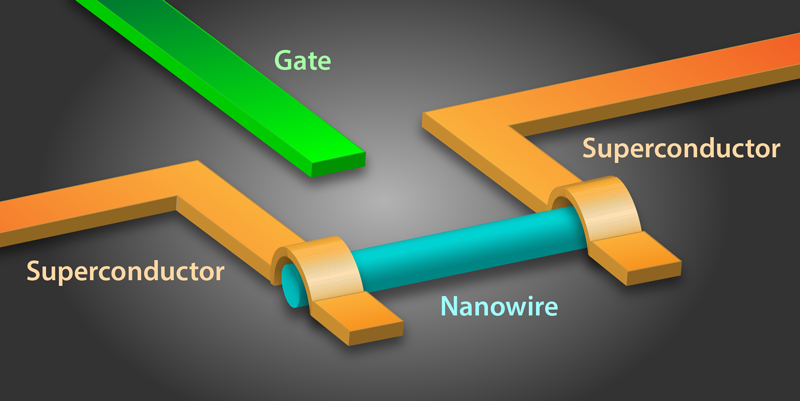
Two independent groups have now demonstrated a new qubit scheme, consisting of two superconductors bridged by a nanowire, that could help researchers design quantum circuits with more flexibility. The teams, led by Leonardo DiCarlo at Delft University of Technology in the Netherlands [1] and Charles Marcus at the University of Copenhagen in Denmark [2], have demonstrated structures in which the nanowire replaces one of the basic elements of a superconducting qubit—the insulating barrier between two superconductors that forms a Josephson junction. The scheme enables the control of the junction properties by an applied electric field, which will lead to superconducting qubits that are easy to tune. The structure might also provide a way to combine the controllability of superconducting qubits with the long coherence times of solid-state spins or future topological qubits.
Today, the most common superconducting qubit is the “transmon” qubit, which consists of a Josephson junction in parallel with a capacitor [3]. The Josephson junction is a superconducting wire interrupted by a short, usually insulating, segment called a “weak link.” The junction serves two purposes. First, it acts as a nonlinear inductor, which, in combination with the capacitor, forms an anharmonic electromagnetic oscillator, whose energy levels are not equally spaced. The oscillator’s ground and first excited states define the |0〉 and |1〉 qubit states that can be manipulated with radio-frequency pulses. Second, the junction allows the control of the qubit resonance frequency. If two junctions are combined in a superconducting loop, the flux of an applied magnetic field through the loop affects the qubit resonance. Tuning the qubit frequency is crucial for many applications: it allows researchers to single out one qubit within an ensemble, entangle multiple qubits by bringing them briefly into resonance, and prevent cross talk in groups of qubits carrying out independent logic operations.
Josephson junctions are typically made from aluminum (Al) superconducting wires and an aluminum oxide barrier. Both groups have instead made transmon qubits in which the aluminum/aluminum oxide junction is replaced by an indium-arsenide (InAs) semiconductor nanowire bridging two superconductors (see Fig. 1). InAs nanowires are ideal for this purpose because they are relatively easy to grow as single crystals and to integrate into superconducting circuits. In particular, the electronic surface states of InAs nanowires enable nearly lossless contacts to a superconductor [4]. To contact the nanowire, Di Carlo’s team uses NbTiN, a superconductor with a high critical magnetic field, while Marcus’ group uses epitaxially grown Al [5].
The teams exploit the semiconducting properties of InAs to tune the qubit resonance frequency by applying an electric field to the nanowire via a nearby gate electrode. The field changes the density of the conduction electrons in the nanowire, shifting the qubit resonance [4]. Both groups demonstrate that an applied gate voltage on the order of 10 volts shifts the qubit frequency over a wide range, from hundreds of megahertz to several gigahertz. These voltage-based tuning schemes significantly simplify the qubit architecture compared to conventional transmon qubits, which require two junctions instead of one as well as on-chip circuitry for generating the tuning magnetic field.
To allow the readout and manipulation of qubits, the researchers embedded the qubit in a cavity—a high-quality-factor superconducting resonator [6]. Both groups demonstrate that the coupling between the nanowire transmons and the cavity can enter the so-called strong-coupling regime of cavity quantum electrodynamics, in which microwave photons in the cavity are strongly coupled to the qubit states. When the qubit and cavity are brought into resonance, a clear hybridization is observed, i.e., the qubit and the cavity behave as a single quantum-mechanical system. In such a regime, the qubit-cavity coupling exceeds the coupling of either the qubit or the cavity to the environment, meaning that individual quanta of energy can be coherently swapped between the qubit and cavity.
Marcus and his collaborators also provide a full characterization of the quantum control achievable with their qubit. They initialize the qubit to the |0〉 state, then apply a microwave field that creates a coherent |0〉−|1〉 superposition, and measure how long the coherent superposition can be maintained. They observe a coherence time of roughly 1 microsecond ( 𝜇s). This value is less than that of state-of-the art Al transmons (exceeding 10𝜇s), but still impressive for this first-generation device. In a computing scheme, such a value implies that roughly 5000 coherent qubit operations can be carried out before the qubit coherence is lost.
These nanowire-based schemes represent an important step toward the creation and understanding of hybrid systems for quantum information processing, offering a promising route for realizing voltage-tuned superconducting qubits. Compared to existing flux-controlled schemes, whose tuning requires flowing currents that dissipate power, the new qubits would be more scalable to larger architectures. Further research, however, needs to assess whether the coherence times can reach those of standard superconducting qubits. But the unique properties of nanowire junctions will be an asset for a number of other applications, such as the study of proximity effects at superconductor/semiconductor interfaces. Another prospect is the possibility of combining these qubits with other types of qubits or quantum systems. These electrically tuned nanowire transmons may be operated at higher magnetic fields than conventional qubits (in particular Di Carlo’s scheme, based on NbTiN, which can withstand much higher magnetic fields than Al without losing superconductivity). This will allow researchers to use them in combination with spin qubits, whose control requires large magnetic fields that would perturb a flux-controlled transmon qubit.
But the most intriguing possibility involves Majorana fermions. These exotic quasiparticles could be used to build a topological quantum computer, in which logic operations take place by “braiding” particles [7]. Researchers believe that InAs nanowires, such as those used to make Josephson junctions in these papers, can host Majoranas [8]. While topological qubits by themselves are not sufficient to build a universal quantum computer [7], recent work has suggested that this could be done by coupling topological qubits to transmons [9]. The new nanowire schemes demonstrated by the groups of DiCarlo and Marcus pose an ideal platform to test such ideas.
This research is published in Physical Review Letters
References
- G. de Lange, B. Van Heck, A. Bruno, D. J. Van Woerkom, A. Geresdi, S. R. Plissard, E. P. A. M. Bakkers, A. R. Akhmerov, and L. DiCarlo, “Realization of Microwave Quantum Circuits Using Hybrid Superconducting-Semiconducting Nanowire Josephson Elements,” Phys. Rev. Lett. 115 (2015).
- T. W. Larsen, K. D. Petersson, F. Kuemmeth, T. S. Jespersen, P. Krogstrup, J. Nygard, and C. M. Marcus, “A Semiconductor Nanowire-Based Superconducting Qubit,” Phys. Rev. Lett. 115 (2015).
- J. Koch, T. M. Yu, J. Gambetta, A. A. Houck, D. I. Schuster, J. Majer, A. Blais, M. H. Devoret, S. M. Girvin, and R. J. Schoelkopf, “Charge-Insensitive Qubit Design Derived from the Cooper Pair Box,” Phys. Rev. A 76, 042319 (2007).
- Y.-J. Doh, J. A. van Dam, A. L. Roest, E. P. A. M. Bakkers, L. P. Kouwenhoven, and S. De Franceschi, “Tunable Supercurrent Through Semiconductor Nanowires,” Science 309, 272 (2005).
- W. Chang, S. M. Albrecht, T. S. Jespersen, F. Kuemmeth, P. Krogstrup, J. Nygård, and C. M. Marcus, “Hard gap in epitaxial semiconductor–superconductor nanowires,” Nature Nanotech. 10, 232 (2015).
- A. Blais, R.-S. Huang, A. Wallraff, S. M. Girvin, and R. J. Schoelkopf, “Cavity Quantum Electrodynamics for Superconducting Electrical Circuits: An Architecture for Quantum Computation,” Phys. Rev. A 69, 062320 (2004).
- J. Alicea, Y. Oreg, G. Refael, F. von Oppen, and M. P. A. Fisher, “Non-Abelian Statistics and Topological Quantum Information Processing in 1D Wire Networks,” Nature Phys. 7, 412 (2011).
- A. Das, Y. Ronen, Y. Most, Y. Oreg, M. Heiblum, and H. Shtrikman, “Zero-Bias Peaks and Splitting in an Al-InAs Nanowire Topological Superconductor as a Signature of Majorana Fermions,” Nature Phys. 8, 887 (2012).
- F Hassler, A. R. Akhmerov, and C. W. J. Beenakker, “The Top-Transmon: A Hybrid Superconducting Qubit for Parity-Protected Quantum Computation,” New J. Phys. 13, 095004 (2011).