Graphene Gets a Good Gap
The invention of silicon semiconductor integrated circuits more than fifty years ago has paved the way for modern electronics and computing. But with more than 10 times better electronic conduction properties than silicon, graphene—a carbon sheet just one atom thick—is considered silicon’s ideal replacement. This “wonder material” promises to deliver electronic devices much smaller, faster, more flexible, and more efficient than their silicon analogs [1]. However, one of the roadblocks to using graphene for making such devices is the lack of a sizeable energy gap, or band gap, in its electronic energy structure. Ed Conrad from the Georgia Institute of Technology and colleagues [2] now show that they have opened a large band gap in a graphene sheet by growing it on the silicon face of a silicon carbide substrate.
The band gap in a semiconductor is the minimum energy required to excite an electron that is stuck in a bound state into a state in which it can participate in conduction. It largely determines the transport and optical properties of the semiconductor. In terms of the material’s electronic energy band structure, the band gap is the energy difference between the top of the valence band and the bottom of the conduction band. The Fermi level, defined as the top of available electron energy levels, is located halfway between these two bands.
Graphene has a peculiar band structure. Its valence and conduction bands, known technically as 𝜋 and 𝜋∗ bands, show a linear (conical) relationship between electron energy and momentum and meet at certain points ( K and K′ in Fig. 1) [1]. This unusual dispersion relationship makes graphene a zero-gap material, which conducts electrons like a metal. But without a gap, there is no way of controlling and stopping the material’s electrons—features that are needed to make electronic circuitry.
Nonetheless, because of graphene’s incredible properties and potential, researchers have been actively searching for ways to create a semiconductor version of the material. Using the method of quantum confinement, band gaps have been engineered in graphene quantum dots [3] and graphene ribbons [4]. The generated band gaps are generally too small, on the order of a few milli-electron-volts. But for extremely narrow ribbons, the gap can reach values as large as 100meV. It is, however, difficult to scale up this narrow form of graphene for mass production.
Among the various methods to make graphene, the technique of epitaxial growth is considered to be a promising route because of its scalability potential. The method involves using high heat to decompose a silicon carbide (SiC) substrate such that it forms one or more carbon layers [5]. So far, attention has mainly been on optimizing the growth of the first electronically active carbon layer, which displays the 𝜋 and 𝜋∗ bands. This graphene layer grows on top of an electronically inert carbon layer, known as the “buffer” layer, which does not exhibit the 𝜋 and 𝜋∗ bands [5, 6] despite having a crystal-lattice structure similar to that of graphene. It is in these epitaxial samples that researchers have managed to open the largest graphene band gap— 0.26eV in size [6]. The band gap in these samples lies well below the Fermi energy. Its opening has been attributed to the breaking of the symmetry of the two carbon sublattices that comprise the graphene layer, which is caused by the interaction between the graphene layer and the substrate [6].
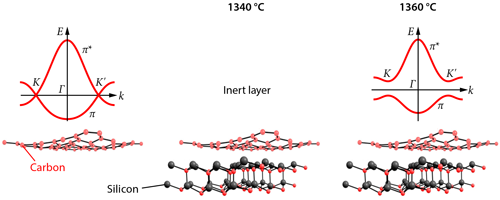
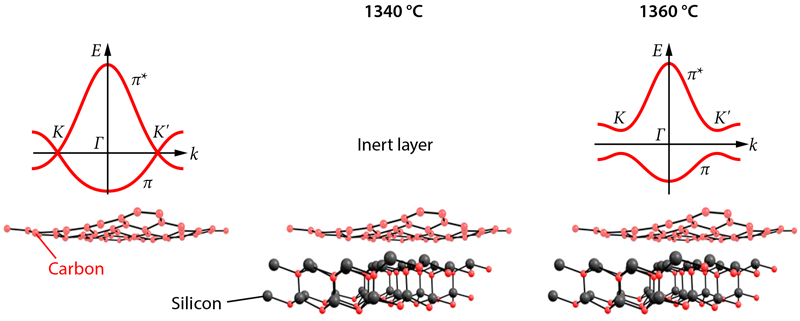
Conrad and colleagues report a band gap in epitaxially grown graphene samples that is about a factor of 2 larger than this previous record value of 0.26eV. What is more, they succeeded in generating a band gap centered around the Fermi level, a fundamental requisite for turning graphene into a practical semiconductor. But a key difference from earlier work is that the authors focused their investigation not on the active layer of the samples but on the buffer layer, exploring a new temperature regime for the growth of the layer. The researchers analyzed their graphene samples using angle-resolved photoemission spectroscopy (ARPES). This is a “photon-in, electron-out technique” that measures the kinetic energy of electrons removed from the samples upon photon irradiation. Therefore, it provides information about the samples’ electronic energy band structure. For samples grown at a temperature of about 1360∘C, the ARPES data revealed 𝜋 and 𝜋∗ bands separated by a gap of at least 0.5eV. However, for a growth temperature about 20∘C lower, the ARPES data did not show any gapped 𝜋 and 𝜋∗ bands. The results indicate that the growth temperature plays a crucial part in defining the electronic character of the buffer layer.
These intriguing observations are in partial agreement with previous studies that investigated the effect of intercalating hydrogen or germanium atoms between the buffer layer and the silicon carbide substrate [7, 8]. These studies showed that the inclusion of the hydrogen or germanium atoms resulted in the appearance of 𝜋 and 𝜋∗ bands in the buffer layer, but in contrast to Conrad and colleagues’ findings, no band gap has been observed in these cases. Also noteworthy is the authors’ finding of anisotropic 𝜋 and 𝜋∗ bands in momentum space. They show that the effective mass and velocity of electrons near the top of the valence band can vary by as much as 50% depending on the electrons’ propagation direction. This anisotropy hasn’t been observed in any previously studied samples of graphene.
The researchers suggest that the opening of the gap and the anisotropy of the 𝜋 and 𝜋∗ bands in their samples is caused by a periodic bonding between the graphene layer and the silicon carbide substrate. Testing this hypothesis, as well as the apparent critical role of sample temperature in turning the first carbon layer into a graphene sheet, will no doubt require further experimental and theoretical work. In the meantime, however, Conrad and co-workers’ results provide another beautiful piece of the puzzle of understanding and manipulating this amazing two-dimensional material and bring us a bit closer to the dream of using graphene to make electronic devices.
This research is published in Physical Review Letters
References
- A. K. Geim and K. S. Novoselov, “The Rise of Graphene,” Nature Mater. 6, 183 (2007).
- M. S. Nevius, M. Conrad, F. Wang, A. Celis, M. N. Nair, A. Taleb-Ibrahimi, A. Tejeda, and E. H. Conrad, “Semiconducting Graphene from Highly Ordered Substrate Interactions,” Phys. Rev. Lett. 115, 136802 (2015).
- B. Trauzettel, D. V. Bulaev, D. Loss, and G. Burkard, “Spin Qubits in Graphene Quantum Dots,” Nature Phys. 3, 192 (2007).
- M. Y. Han, B. Özyilmaz, Y. Zhang, and P. Kim, “Energy Band-Gap Engineering of Graphene Nanoribbons,” Phys. Rev. Lett. 98, 206805 (2007).
- C. Berger et al., “Ultrathin Epitaxial Graphite: 2D Electron Gas Properties and a Route Toward Graphene-Based Nanoelectronics,” J. Phys. Chem. B 108, 19912 (2004).
- S. Y. Zhou, G.-H. Gweon, A. V. Fedorov, P. N. First, W. A. de Heer, D.-H. Lee, F. Guinea, A. H. Castro Neto, and A. Lanzara, “Substrate-Induced Bandgap Opening in Epitaxial Graphene,” Nature Mater. 6, 770 (2007).
- C. Riedl, C. Coletti, T. Iwasaki, A. A. Zakharov, and U. Starke, “Quasi-Free-Standing Epitaxial Graphene on SiC Obtained by Hydrogen Intercalation,” Phys. Rev. Lett. 103, 246804 (2009).
- S. Forti, K. V. Emtsev, C. Coletti, A. A. Zakharov, C. Riedl, and U. Starke, “Large-Area Homogeneous Quasifree Standing Epitaxial Graphene on SiC(0001): Electronic and Structural Characterization,” Phys. Rev. B 84, 125449 (2011).