Caught in the Tube
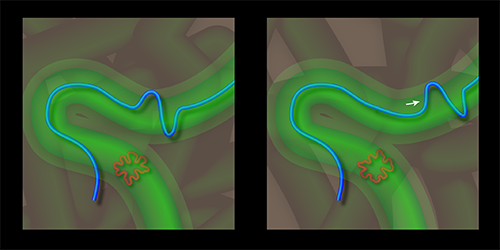
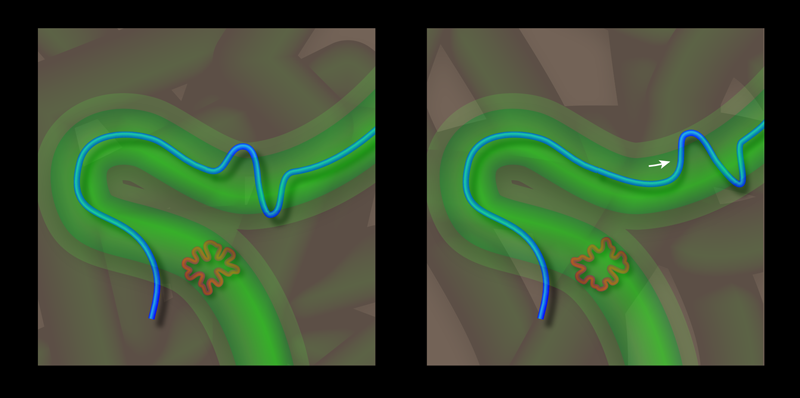
Molten forms of entangled polymer chains are used in many industrial processes, such as the coating of protective films or the molding of plastics. The ability to predict how these “polymer melts” will stretch and pour—their rheology—is thus a technologically relevant problem. For decades, physicists have modeled polymers using reptation theory [1, 2]. This treats each polymer chain like a snake moving in a narrow tube (Fig. 1) whose diameter characterizes the confining effects of surrounding molecules. A team led by Dieter Richter at the Forschungszentrum Jülich, Germany, has now succeeded in measuring the diameter of the tube directly [3]. This value, which was difficult to measure accurately before, can be used to quantitatively test the predictions of polymer models and to make the processing of macromolecular materials more efficient.
Polymer melts are viscoelastic. Unlike a spring, which stretches in direct proportion to how hard it is pulled, viscoelastic materials have a time-dependent response to stress. Under a small, constant stress, such as a shear force, the melt initially has no apparent response (glassy behavior) and then starts to deform by larger and larger amounts. Eventually, the deformation will plateau and the melt will respond like a rubber band. If the stress persists beyond the longest time it takes the polymer chain to relax to equilibrium, the material will start to flow like a liquid. A key theoretical challenge is to figure out how these macroscopic structural effects depend on the properties of the individual chains, such as length and topology.
Starting in the early 1950s, physicists developed a number of models to do exactly this. The Rouse model describes chemically bonded monomers like beads connected by springs and predicts that chains relax via a series of increasingly longer-wavelength longitudinal vibrational modes [4]. In principle, Rouse’s model can describe all of the chains in a polymer melt, but the enormous number of elements involved makes the problem difficult to solve. A breakthrough came from realizing that the confining effects of the melt on a single chain can be approximated by assuming the chain is restricted to moving in a tube: the narrower the tube, the fewer modes of relaxation available to the chain [5]. Pierre-Gilles de Gennes showed that chains can escape the tube via reptation, a movement similar to that of snakes sliding on the ground [1]. Chains relax along the tube via longitudinal modes, while transversal waves exceeding the tube diameter are suppressed. Today, the tube model is the basis of most theoretical predictions in polymer dynamics, such as the relation between relaxation time and polymer length [6–8], though agreement with experiment usually requires a more detailed microscopic description.
Although the tube is a mathematical construct, its diameter can be measured. This is done by comparing the diffusion of a “test chain” in a melt to the diffusion it would undergo in a free environment. The complication is that, as de Gennes showed, chains reptate. So experiments convolute the motion of the chain along the length of the tube with motion in the transverse direction and therefore tend to overestimate the tube’s diameter (Fig. 1).
Richter and his colleagues have resolved this problem by using ring-shaped polymers as the test chain. They discovered that when a ring is immersed in a large number of linear chains made of the same monomer, its dynamics become enslaved to that of the host: the movement of the ring segments strictly follows that of the monomers of linear macromolecules. But because the monomers of a ring form a closed loop, they cannot reptate along the tube. The ring’s motion therefore serves as a perfect probe of the true diameter of the tube.
In their experiments, Richter and his colleagues studied polymer melts of linear chains containing a small concentration (1–10% by volume) of ring-shaped polymers. The authors measured the diffusion of the ring molecule over time using the neutron spin echo technique. This powerful tool, which is widely used to study polymer dynamics, measures the motion of nuclei in a sample by detecting its effect on the precession of polarized spins in a neutron beam. The technique is sensitive to molecular motion at the nanoscale and on the long time scales characteristic of reptation—in this case, up to 600 nanoseconds. The team was able to isolate the motion of the rings by labeling them with deuterium, which, for a neutron probe, provides contrast against the hydrogen-based linear chains.
By analyzing their spin echo data, Richter’s group concluded that ring-shaped polymers were confined in a tube nanometers (nm) wide. The authors compared this value with that obtained by a previous study [9] of linear test chains that were also tagged with deuterium, which found the tube had a larger effective diameter of . Since diffusion rates scale with the area of the tube, this implies rings can explore a surface smaller than that of linear chains. This factor of close to 2/3 has a simple explanation. Because rings only fluctuate transverse to their circumference, they can only relax in two of the three dimensions of the tube. The authors’ measurements are therefore self-consistent with the tube model.
Having a technique that can measure the tube dimensions quantitatively could help researchers answer several questions about polymer dynamics. For example, the approach developed by Richter’s group could be used to understand the phenomenon of “tube dilation” in branched polymers, such as star- and comb-shaped polymers, in which the tube grows larger as individual branches relax. Similarly, an advanced version of the technique, capable of characterizing nanoscopic samples, could probe the reduction in chain-entanglement density that occurs when a melt is confined in a layer of nanoscale thickness, like those formed by spin coating [10]. In these systems, chains overlap less than in unconfined melts and therefore move in effectively wider tubes. Surprisingly, this condition persists up to time scales exceeding by some orders of magnitude those of reptation [11].
From an applications standpoint, the approach could be used to make more accurate predictions in the fabrication of plastics. Manufacturing processes require exact control of the flow of polymers melts within long pipes, in which the raw materials are prepared to achieve their final shape. To reduce production costs, the viscosity of the melt, which can be derived from the tube diameter, needs to be known accurately.
This research is published in Physical Review Letters.
References
- P. G. de Gennes, “Reptation of a Polymer Chain in the Presence of Fixed Obstacles,” J. Chem. Phys. 55, 572 (1971).
- A. E. Likhtman and T. C. B. McLeish, “Quantitative Theory for Linear Dynamics of Linear Entangled Polymers,” Macromolecules 35, 6332 (2002).
- S. Gooßen, M. Krutyeva, M. Sharp, A. Feoktystov, J. Allgaier, W. Pyckhout-Hintzen, A. Wischnewski, and D. Richter, “Sensing Polymer Chain Dynamics through Ring Topology: A Neutron Spin Echo Study,” Phys. Rev. Lett. 115, 148302 (2015).
- P. E. Rouse, “A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers,” J. Chem. Phys. 21, 1272 (1953).
- S. F. Edwards, “The Statistical Mechanics of Polymerized Material,” Proc. Phys. Soc. 92, 9 (1967).
- S. T. Milner and T. C. B. McLeish, “Reptation and Contour-Length Fluctuations in Melts of Linear Polymers,” Phys. Rev. Lett. 81, 725 (1998).
- M. Rubinstein and R. H. Colby, “Self-Consistent Theory of Polydisperse Entangled Polymers: Linear Viscoelasticity of Binary Blends,” J. Chem. Phys. 89, 5291 (1988).
- M. Doi, “Explanation for the 3.4 Power Law of Viscosity of Polymeric Liquids on the Basis of the Tube Model,” J. Polym. Sci., Polym. Lett. Ed. 19, 265 (1981).
- K. Niedzwiedz, A. Wischnewski, W. Pyckhout-Hintzen, J. Allgaier, D. Richter, and A. Faraone, “Chain Dynamics and Viscoelastic Properties of Poly(ethylene oxide),” Macromolecules 41, 4866 (2008).
- S. Napolitano, S. Capponi, and B. Vanroy, “Glassy Dynamics of Soft Matter Under 1D Confinement: How Irreversible Adsorption Affects Molecular Packing, Mobility Gradients and Orientational Polarization in Thin Films,” Eur. Phys. J. E 36, 61 (2013).
- D. R. Barbero and U. Steiner, “Nonequilibrium Polymer Rheology in Spin-Cast Films,” Phys. Rev. Lett. 102, 248303 (2009).