Sharing Quantum States
Forms of collective behavior often emerge in large ensembles of interacting units, such as a network of neurons, a flock of birds, or electrons in solids. In condensed-matter systems, the emergence of these collective phenomena is often associated with spectacular properties that could be harvested in applications. But the complexity of the underlying many-body interactions makes it difficult to both understand and control such effects.
Now, Clemens Rössler, at the Swiss Federal Institute of Technology (ETH) in Zurich, and co-workers [1] have shown that it is possible to control a prototypical many-body effect—the Kondo effect—in a system made of a quantum dot embedded in an electronic cavity. By tuning the coupling between the dot and the cavity, the researchers can bring the electrons in the dot together with the cavity’s electrons to form a unique quantum state with a total spin of 0—a spin-singlet. The scheme, which is controllable by purely electrical means, may allow the faithful transfer of quantum states across distant qubits, serving as a “quantum bus” in quantum processing architectures.
The authors’ approach is based on the ability to control the occurrence of the Kondo effect in the dot-cavity system. In metals, the Kondo effect arises from the interaction of a magnetic impurity, like a defect with an unpaired electron, with the metal’s Fermi sea of electrons. At low temperatures, the unpaired electron and the delocalized electrons in the metal couple to form a spin singlet. The Kondo effect explains the low-temperature downturn in the conductivity of metals and plays a role in important condensed-matter systems, from heavy-fermion materials to high-temperature superconductors.
As already anticipated by theoretical studies in the late 1980s [2], in 1998 David Goldhaber-Gordon and co-workers demonstrated that the Kondo singlet state can be achieved, rather than in an impurity, in a much more controllable system: a quantum dot in a metal [3]. As the surrounding electrons scatter into and out of the quantum dot with a small probability, they may flip the magnetic moment (spin) of an electron in the dot, before returning to the Fermi sea. This many-electron dance screens the local moment of the electron spin and delocalizes it into the surrounding electron sea for temperatures lower than a characteristic energy scale (quantified by the Kondo temperature).
The Kondo temperature in such a system depends on the probability with which the surrounding electrons tunnel into and out of the dot, as well as on the availability of electronic states into which the electrons are allowed to scatter. Thus, controlling how the dot and cavity electrons are connected is key to adjusting the Kondo temperature and the resulting Kondo state. Different groups have used this dot-cavity system to study the Kondo state, exploring its dependence on the number of electrons in the dot and investigating nonequilibrium regimes created by applying large currents or irradiating the dot with microwaves.
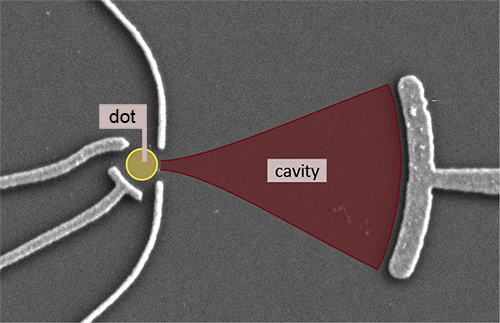
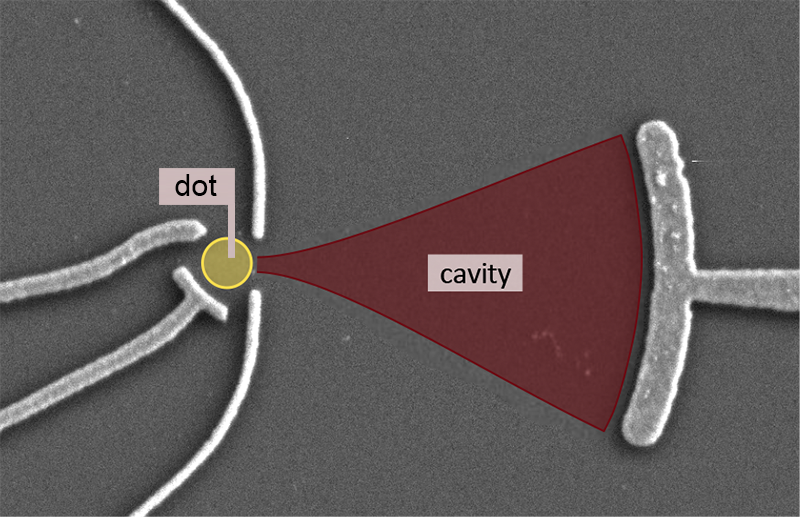
Rössler and co-workers now demonstrate a new level of control of many-body Kondo effects in a quantum dot. Their key idea is to engineer not only the electronic states of the dot, but also those of its environment. The team engineered their scheme on a semiconductor chip, placing a quantum dot in an electronic cavity that uses mirrors to confine a two-dimensional gas of electrons (see Fig. 1). These mirrors are curved metallic surfaces that reflect or attract electrons depending on an applied voltage, and they have been used to steer electrons in two-dimensional structures [4]. Placed opposite one another, two mirrors can create quasistationary states with enhanced amplitudes in the region between them. Such confined states are akin to those of an optical cavity, except that here the amplitudes are those of electronic wave functions, rather than of an optical field. Typically, these mirrors are thought to act on individual electrons. Rössler et al., however, show for the first time that such mirrors can be used to focus collective electronic states, such as Kondo states.
By applying voltages to different electrodes, the authors are able to control how many electrons occupy the dot, tune the reflectivity of the mirror, and measure the dot conductance. Under the right voltage conditions, the structure becomes a resonant electronic cavity for the two-dimensional electron gas [5]. By tuning the coupling between mirror and cavity, the researchers direct cavity electrons to “rob” the local moment from the dot and its electrodes. Under these conditions, the system enters an entirely different quantum state.
In a regime where the quantum dot interacts predominantly with the electrons in the electrodes (and much less with the cavity), the cavity and the electrodes form a Kondo state, as evident from characteristic conductance signatures: around a bias voltage of zero, the dot exhibits a prominent peak of conductivity, which results from the effective screening of the dot local moment by the Fermi sea. In contrast, when the dot interacts more strongly with the cavity, the Kondo conductance peak in the dot splits into two peaks, and it is increasingly suppressed by the dominant competition of the cavity electrons. This reveals that the singlet state is now shared between the dot and the entire cavity. The effect is reminiscent of the behavior of magnetic impurities in small metallic crystals [6, 7], although the tunability of quantum dot systems [8] is proven here to be much more flexible.
Further studies will need to address a number of outstanding fundamental questions on many-body Kondo physics. Once the dot-cavity coupling is turned on, what are the speed and microscopic mechanisms by which the Kondo correlations between electrons are transferred from the electrodes to the cavity? And is the resulting singlet state truly delocalized over the entire cavity and evenly shared by all the system components—the dot, the cavity, and the electrodes?
Finally, the demonstrated scheme might have implications for quantum processing applications. One can envision quantum computing architectures in which multiple qubits communicate via mirror configurations similar to those employed by the authors. Such schemes could control quantum electronic states, project them over mesoscopic distances, and couple them to the internal degrees of freedom of charge or spin qubits. The sharing of Kondo correlations could thus lead to general strategies for sharing quantum information.
This research is published in Physical Review Letters.
References
- C. Rössler et al., “Transport Spectroscopy of a Spin-Coherent Dot-Cavity System,” Phys. Rev. Lett. 115, 16603 (2015).
- L. I. Glazman and M. E. Raikh, “Resonant Kondo Transparency of a Barrier with Quasilocal Impurity States,” JETP Lett. 47, 452 (1988), http://www.jetpletters.ac.ru/ps/1095/article_16538.shtml; Tai Kai Ng and Patrick A. Lee, “On-Site Coulomb Repulsion and Resonant Tunneling,” Phys. Rev. Lett. 61, No. 15, 1768 (1988).
- D. Goldhaber-Gordon, H. Shtrikman, D. Mahalu, D. Abusch-Magder, U. Meirav, and M. A. Kastner, “Kondo Effect in a Single-Electron Transistor,” Nature 391, 156 (1998).
- J. Spector, H. L. Stormer, K. W. Baldwin, L. N. Pfeiffer, and K. W. West, “Electron Focusing in Two-Dimensional Systems by Means of an Electrostatic Lens,” Appl. Phys. Lett. 56, 1290 (1990).
- Similar schemes have previously been used to investigate weak charging effects as well as long-range interactions of magnetic moments. See: S. Amasha, I. G. Rau, M. Grobis, R. M. Potok, H. Shtrikman, and D. Goldhaber-Gordon, “Coulomb Blockade in an Open Quantum Dot,” Phys. Rev. Lett. 107, 216804 (2011); N. J. Craig, J. M. Taylor, E. A. Lester, C. M. Marcus, M. P. Hanson, and A. C. Gossard, “Tunable Nonlocal Spin Control in a Coupled-Quantum Dot System,” Science 304, 565 (2004).
- W. B. Thimm, J. Kroha, and J. von Delft, “Kondo Box: A Magnetic Impurity in an Ultrasmall Metallic Grain,” Phys. Rev. Lett. 82, 2143 (1999).
- P. S. Cornaglia and C. A. Balseiro, “Spectral Densities of Kondo Impurities in Nanoscopic Systems,” Phys. Rev. B 66, 174404 (2002).
- L. G. G. V. Dias da Silva, N. P. Sandler, K. Ingersent, and S. E. Ulloa, “Zero-Field Kondo Splitting and Quantum-Critical Transition in Double Quantum Dots,” Phys. Rev. Lett. 97, 096603 (2006).