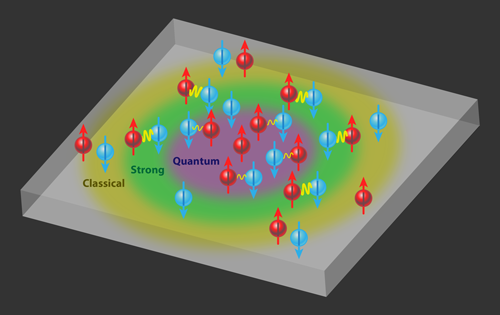
Journey from Classical to Quantum in Two Dimensions
One of the major challenges in physics today is to describe the behavior of many interacting quantum particles. What makes this problem especially hard is when the motion of the interacting quantum particles is severely restricted by the intrinsic structure of the material. This is true in 2D materials like graphene and in layered structures that exist in exceptionally high-temperature superconductors. Such 2D systems feature strongly enhanced interactions compared to 3D and are notoriously difficult to treat theoretically. Now, two experimental groups have extracted fundamental statistical information about the properties of interacting atoms confined to move in a plane. Chris Vale and colleagues from Swinburne University, Australia [1], as well as Tilman Enss and collaborators from Heidelberg University, Germany [2], have measured the equation of state for fermionic atoms in two dimensions (2D), thus determining the relationship between temperature, particle density, and interaction strength. This equation of state reveals the peculiar nature of 2D, where quantum mechanics can fundamentally change the character of interactions, and it provides an important benchmark for theories of two-dimensional interacting systems.
Since the 19th century, physicists have exploited the powerful fact that a single equation can describe the thermodynamics of many substances, even when the constituent particles are very different. A classic example is the ideal gas law, an equation of state that neglects the interparticle interactions and applies to all gases of atoms or molecules at high enough temperatures (corresponding to room temperature in many cases). However, it quickly becomes challenging to construct theories of many-particle systems at lower temperatures, where the quantum nature of the particles and the interactions between them play a significant role.
The situation is even more complex if the particle motion is constrained to lower dimensions such as 2D, giving rise to strikingly different behavior as the gas evolves from classical to quantum. For instance, when the interactions between particles are short ranged, a 2D system of classical particles behaves as if there is no length scale associated with the interactions, unlike in 3D. However, for quantum particles, the uncertainty principle always guarantees a finite length scale: for the case of attractive interactions, it is set by the two-body (dimer) bound state [3]. This length scale becomes apparent in the equation of state as the temperature is lowered (or, equivalently, the density is increased) such that the de Broglie wavelength of the particles approaches the interparticle separation and the gas enters the quantum regime.
Experiments on optically and magnetically trapped ultracold atoms provide a unique test bed in which to investigate the behavior of such 2D quantum gases since they can be tuned across a range of interactions and temperature regimes [4]. If the quantum particles are fermions, the physics is particularly rich, since the Pauli exclusion principle provides an additional form of interaction between particles. In this case, the interplay between Fermi statistics and attractive interactions gives rise to a crossover from a weakly attractive Fermi gas to a Bose gas of tightly bound dimers as the attraction is increased [3, 5]. Below a critical temperature, the system eventually undergoes a transition to a superfluid phase [6]. Within this low-temperature regime, the equation of state has already been probed experimentally [7] and was found to be consistent with the behavior expected from theories at zero temperature [5]. However, it has remained an open question how the 2D equation of state evolves with temperature.
To address this point, the groups in Swinburne and Heidelberg have had to combine two innovative approaches. First, they have employed a highly anisotropic trapping potential that effectively freezes out motion in one direction and only allows atoms to move freely within a single plane (see Fig. 1). The weak in-plane trapping potential creates a region of high atom density at the trap center, where quantum effects are significant, while leaving the trap edges at low density, where the system behaves like a classical high-temperature gas. By measuring the atom number as a function of position in the plane, they were thus able to probe a wide range of parameter phase space in a single cloud. Second, they constrained errors in the temperature and other experimental observables by using known thermodynamic relations between these quantities, similar to what was done in earlier 3D experiments [8]. In particular, they could extract the temperature of their 2D gas by fitting the classical outer edge of the atom cloud to an exact high-temperature equation of state that builds on the ideal gas law.
Following such a protocol, the two teams have produced complementary studies of how the particle density depends on temperature and chemical potential: the Swinburne group has focused on the weakly attractive regime while the Heidelberg team’s experiment spans the crossover to a Bose gas of dimers. In both cases, this 2D equation of state clearly displays the impact of the dimer bound state. By comparing the density with that expected for an ideal (noninteracting) Fermi gas, it becomes apparent that the attractive interactions produce the largest density enhancement in the region between the quantum center and the classical edge. This implies that the particle interactions are strongest here in this intermediate location, where the characteristic distance between particles approaches the scale set by the de Broglie wavelength. For higher densities, the effect of interactions diminishes as the interparticle distance becomes small with respect to the dimer state. This behavior is strikingly absent in previous studies of 2D Bose gases [9] and in recent 3D Fermi gas experiments [8], where the strongest interactions occur in the quantum regime.
These experiments are just the beginning. Knowledge of the equation of state for a 2D Fermi gas can be used to develop theories of strongly interacting fermions, and it can provide a basis for describing phenomena beyond the equilibrium case, such as spin dynamics [10]. However, there is also a hidden richness here, namely, the fact that the 2D gas is embedded in three dimensions. The layer thickness then corresponds to another tuning knob for the interactions, which could, for example, be used to test whether superfluidity exists at a higher temperature when the gas lies between 2D and 3D [11].
This research is published in Physical Review Letters.
References
- K. Fenech, P. Dyke, T. Peppler, M. G. Lingham, S. Hoinka, H. Hu, and C. J. Vale, “Thermodynamics of an Attractive 2D Fermi Gas,” Phys. Rev. Lett. 116, 045302 (2016).
- I. Boettcher, L. Bayha, D. Kedar, P. A. Murthy, M. Neidig, M. G. Ries, A. N. Wenz, G. Zürn, S. Jochim, and T. Enss, “Equation of State of Ultracold Fermions in the 2D BEC-BCS Crossover,” Phys. Rev. Lett. 116, 045303 (2016).
- M. Randeria, J.-M. Duan, and L.-Y. Shieh, “Bound States, Cooper Pairing, and Bose Condensation in Two Dimensions,” Phys. Rev. Lett. 62, 981 (1989).
- I. Bloch, J. Dalibard, and W. Zwerger, “Many-body Physics with Ultracold Gases,” Rev. Mod. Phys. 80, 885 (2008).
- J. Levinsen and M. M. Parish, “Strongly interacting two-dimensional Fermi gases,” Ann. Rev. Cold Atoms Mol. 3, 1 (2015).
- P. A. Murthy, I. Boettcher, L. Bayha, M. Holzmann, D. Kedar, M. Neidig, M. G. Ries, A. N. Wenz, G. Zürn, and S. Jochim, “Observation of the Berezinskii-Kosterlitz-Thouless Phase Transition in an Ultracold Fermi Gas,” Phys. Rev. Lett. 115, 010401 (2015).
- V. Makhalov, K. Martiyanov, and A. Turlapov, “Ground-State Pressure of Quasi-2D Fermi and Bose Gases,” Phys. Rev. Lett. 112, 045301 (2014).
- M. J. H. Ku, A. T. Sommer, L. W. Cheuk, and M. W. Zwierlein, “Revealing the Superfluid Lambda Transition in the Universal Thermodynamics of a Unitary Fermi Gas,” Science 335, 563 (2012).
- R. Desbuquois, T. Yefsah, L. Chomaz, C. Weitenberg, L. Corman, S. Nascimbène, and J. Dalibard, “Determination of Scale-Invariant Equations of State without Fitting Parameters: Application to the Two-Dimensional Bose Gas Across the Berezinskii-Kosterlitz-Thouless Transition,” Phys. Rev. Lett. 113, 020404 (2014).
- M. Koschorreck, D. Pertot, E. Vogt, and M. Köhl, “Universal Spin Dynamics in Two-Dimensional Fermi Gases,” Nature Phys. 9, 405 (2013).
- A. M. Fischer and M. M. Parish, “Quasi-Two-Dimensional Fermi Gases at Finite Temperatures,” Phys. Rev. B 90, 214503 (2014).