Connecting the Bright and Dark Sides of Galaxies

Arthur Kosowsky

Viewpoint

Connecting the Bright and Dark Sides of Galaxies

Department of Physics and Astronomy, University of Pittsburgh, 3941 O'Hara Street, Pittsburgh, PA 15260, USA

November 9, 2016• Physics 9, 130

A universal law shows that the rotation of a disk galaxy is determined entirely by the visible matter it contains, even if the disk is mostly filled with dark matter.

Figure caption — **Figure 1:** (Top) Near-infrared image of the Sculptor galaxy, an example of a disk galaxy. (Bottom) McGaugh *et al.* [1] have derived a universal law governing the rotation of disk galaxies. The law indicates that the rotation of such galaxies is specified by the visible matter it contains, even if the galaxy is mostly composed of dark matter.

Compared to other types of galaxies, disk-shaped galaxies (disk galaxies) have the simplest dynamics. This makes them ideal for studying the relationship between gravitational forces and the motion of astrophysical bodies within galaxies. Stacy McGaugh and Federico Lelli of Case Western Reserve University, Ohio, and James Schombert of the University of Oregon, Eugene, have shown a simple relation between the rotational acceleration of these galaxies and the distribution of the ordinary (baryonic) matter they contain [1]. Since dark matter is the main component of these galaxies—and thus the main determinant of galactic rotation—this finding implies that the distribution of conventional matter in the disk specifies the density profile of the surrounding dark matter halo.

Many disk galaxies have rotational symmetry: the stars move with constant speed along circular orbits with constant gravitational potential. If these galaxies contained only conventional matter, the gravitational pull from matter should decrease with the radial distance from the galaxy’s center, with a corresponding decrease in velocity. However, almost all disk galaxies exhibit rotational speeds that increase and eventually approach a constant value as the radius increases. This suggests there is more matter in these galaxies than we can see, matter we describe as dark matter. Disks with low mass density (known as low-surface-brightness galaxies) are the most extreme example. They can have hundreds of times more dark matter than ordinary matter, and their mass densities are dominated by dark matter at all radii.

The first observations that signaled the presence of dark matter in disk galaxies were made by Vera Rubin and Kent Ford [2] in the 1970s. Shortly after, Brent Tully and Richard Fisher [3] showed a connection between visible and dark matter: the luminosity of a disk galaxy, proportional to its mass in visible matter, depends as a power law on its rotational velocity at large radii, determined primarily by its dark matter content.

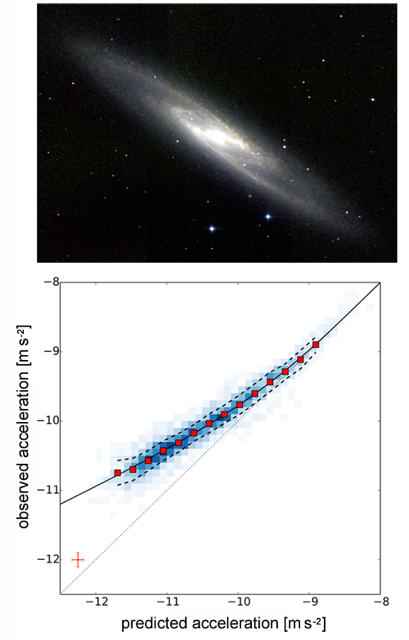
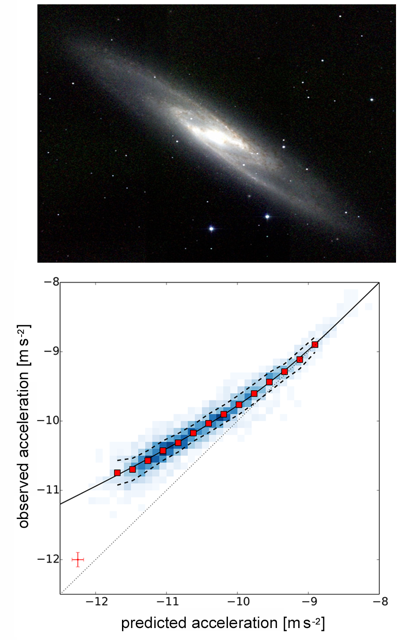
The connection between normal matter and dark matter goes further than the Tully-Fisher relation, however. McGaugh, Lelli, and Schombert have displayed a remarkably simple relation between the radial distribution of visible matter in disk galaxies and the radial dependence of the rotational velocity. The authors analyzed 153 disk galaxies spanning an unprecedented range of masses and densities. The data come from the SPARC (Spitzer Photometry and Accurate Rotation Curves) data set [4], acquired using NASA’s Spitzer telescope, and they were combined with rotation curve measurements from many other sources. The team used infrared-wavelength observations to estimate the visible mass distribution within each galactic disk: the near-infrared luminosity at 3.6 $𝜇$ m is a good tracer of the visible matter content. Then for each radius in a given disk, they computed two quantities: the centripetal acceleration expected from the gravitational pull of the visible matter and the actual centripetal acceleration determined from the measured rotational velocity.

From the 153 galaxies, the authors derive about 2700 data points of the predicted and actual acceleration at different radii within each galaxy’s disk. When plotted against each other, the predicted and measured accelerations trace out a tight relation: if you know the centripetal acceleration at a given radius expected from the gravity of the visible matter in the disk, you then also know the actual acceleration at that radius, even though in many cases it is mostly determined by the dark matter. The authors show that data for all disk galaxies fall on the same curve (see Fig. 1, bottom). Individual galaxies fall along different sections of the curve, depending on their disk mass and surface brightness. This remarkable relation includes galaxies spanning factors of 10,000 in disk mass and 1000 in disk density.

The curve reveals two regimes that depend on the visible versus dark matter content ratio. For values larger than a characteristic acceleration of about $3 \times 1 0^{9} m ∕ s^{2}$ , the observed acceleration equals the acceleration expected from the disk’s visible mass. This corresponds to the inner regions of large galaxies with relatively dense disks, where visible matter dominates. Below this acceleration scale, the observed acceleration becomes systematically higher than that expected from the disk mass, with the difference increasing as the expected disk acceleration gets smaller. The difference is the signature of dark matter. It is worth noting that both the Tully-Fisher relation and the flatness of rotation curves at large radii are contained in the author’s more general scaling relation.

Why should the visible matter in the disk have such a tight correlation with the distribution of surrounding dark matter, over a wide range of disk masses and densities? Some scaling relation connecting disk mass and total mass, like Tully-Fisher, might be expected from the standard cosmological model, because it is reasonable that more massive dark matter halos host more massive galaxy disks. However, the new general relationship, which encompasses both mass and density, is harder to understand. Why should disks of different density at constant mass follow the same scaling relation as disks of different masses at constant density? And why is acceleration the relevant scaling parameter?

No clear answers have been advanced, even though some aspects of this scaling relation have been known, with gradually improving errors, for many years. One possibility is that the observed relation is simply the natural end result of the astrophysical evolution of galaxy disks and dark matter. Cosmological simulations are only now attaining sufficient mass resolution and a sufficiently realistic astrophysical description to produce plausible-looking disk galaxies. The work by McGaugh, Lelli, and Schombert provides a clearly defined and easily computed benchmark for testing whether galaxies in simulations match observations. Current simulations seem to produce similar scaling relations between expected and measured acceleration [5, 6]. But it remains to be seen whether the simulations match the data in detail over the entire range of disk galaxies.

Any alternative explanation is more radical. Dark matter may have more complex physics than assumed by the simplest models, such as additional self-interactions or interactions with normal matter. Or Newtonian gravity may not hold: the scaling relationship could reflect a modification of the Newtonian gravitational force law rather than the presence of dark matter. Mordehai Milgrom has advocated this possibility since 1984 [7], and Jacob Bekenstein demonstrated one possible covariant theory containing such a modification [8]. The modification of Newtonian gravity sidesteps any difficulties in relating dark matter to visible matter in galaxies. But even if a modification of gravity can reproduce observed galaxy dynamics, it generally runs into serious difficulties matching observations on cosmological scales, including the growth of structure, galaxy clusters, gravitational lensing, and driven acoustic oscillations in the microwave background power spectrum.

The observed acceleration relation in disk galaxies presents a clear challenge for simulations of galaxy formation within the standard cosmological model. It will lead us to a deeper understanding of the astrophysical processes shaping galaxies, or—just possibly—to a substantial revision of fundamental physics theories.

This research is published in Physical Review Letters.

References

S. S McGaugh, F. Lelli, and J. M. Schombert, “Radial Acceleration Relation in Rotationally Supported Galaxies,” Phys. Rev. Lett. 117, 201101 (2016).
V. C. Rubin and W. K.Ford, “Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions,” Astrophys. J. 159, 379 (1970).
R. B. Tully and J. R. Fisher, “A New Method of Determining Distances to Galaxies,” Astron. Astrophys. 54, 661 (1977).
F. Lelli, S. S. McGaugh, and J. M. Schombert, “SPARC: Mass Models for 175 Disk Galaxies with Spitzer Photometry and Accurate Rotation Curves,” arXiv:1606.09251; Astron. J. (to be published).
B. W. Keller and J. W. Wadsley, “La Fin du MOND? $Λ$ CDM is Fully Consistent with SPARC Acceleration Law,” arXiv:1610.06183.
A. D. Ludlow et al., “The Mass-Discrepancy Acceleration Relation: A Natural Outcome of Galaxy Formation in CDM Halos,” arXiv:1610.07663.
M. Milgrom, “A Modification of the Newtonian Dynamics as a Possible Alternative to the Hidden Mass Hypothesis,” Astrophys. J. 270, 365 (1983).
J. Bekenstein, “Relativistic Gravitation Theory for the Modified Newtonian Dynamics Paradigm,” Phys. Rev. D 70, 083509 (2004).

About the Author

Arthur Kosowsky is Professor of Physics and Astronomy at the University of Pittsburgh, and Associate Director of the Pittsburgh Particle Physics, Astrophysics, and Cosmology Center (PITT PACC). His research focuses on cosmology, gravitation, and high-energy physics. He is known particularly for work on the cosmic microwave background radiation, and he is a member of the Atacama Cosmology Telescope and the Simons Observatory collaborations to map the microwave sky.