Membrane Holes Can Shrink, Grow, or Stay Put
A hole or pore in the membrane of a biological cell can allow nutrients to enter or a virus to invade, and theorists can predict the stability of such holes. These predictions are difficult to test experimentally, but now researchers have designed a model system using polymer films perforated by an array of different-sized pores. By visually tracking the size of the pores, the team could identify the critical radius at which the pores neither grow nor shrink. The results could help explain the molecular architecture of cell membranes.
Pore formation in a membrane is like the growth of an ice crystal in water at freezing temperatures. The cold water lowers its internal energy when water molecules stick to the crystal seed, so we’d expect the volume of ice to grow continuously. However, there is surface tension at the ice-water boundary, which leads to resistance to any increase in surface area. As a result, ice crystals shrink unless they are larger than some minimum critical radius.
Membrane pores work similarly, says Kari Dalnoki-Veress, from McMaster University in Hamilton, Canada. The area of the pore is like the volume of the ice crystal. An increase in the pore size lowers the internal energy because it reduces the area of the interface between the membrane and the surrounding medium. But this tendency is countered by the edge tension at the rim of the pore, which exerts a shrinking force. The edge tension dominates for small pores, causing them to close, whereas larger pores grow. The critical radius separating growth and collapse depends on the membrane thickness, with thinner membranes typically having a smaller critical radius.
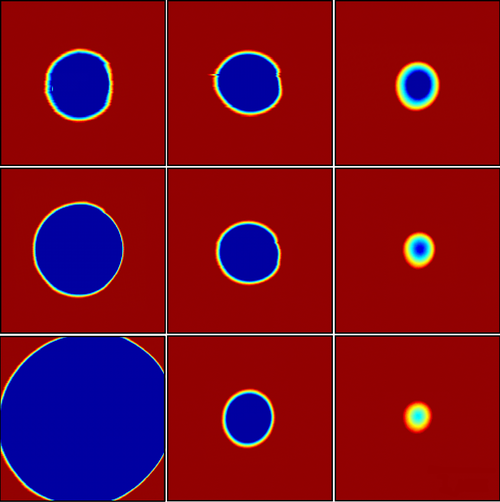
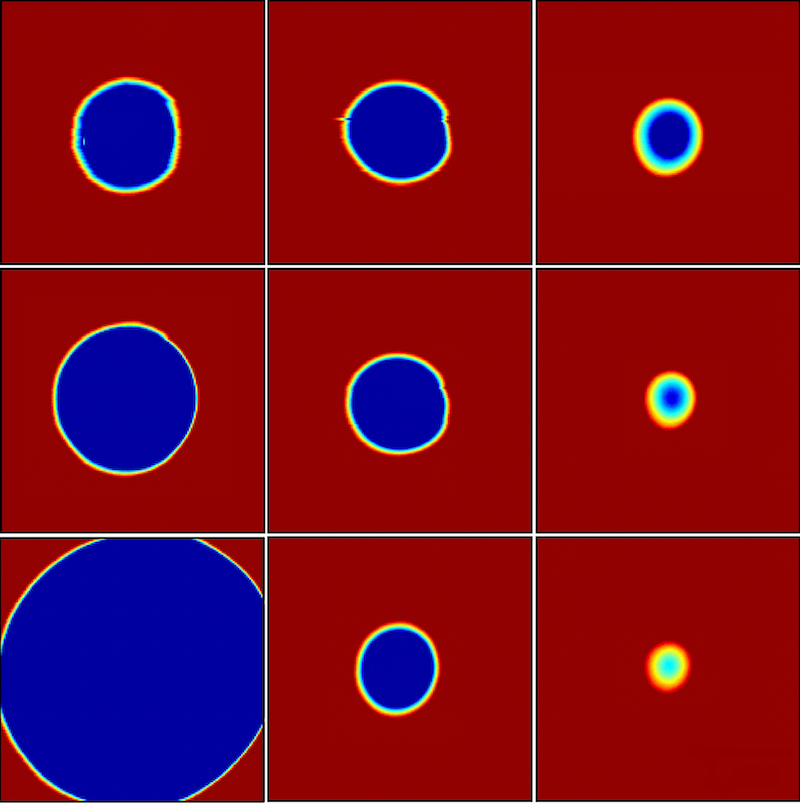
This simple membrane model has never been put to a direct test. Biological membranes have nanometer-sized pores, which are difficult to observe and manipulate. Dalnoki-Veress and his colleagues created a model system with a polymer film that was about a micrometer thick. The stable pore size in this case was in the micrometer range, so the researchers could directly observe pores with an optical microscope.
The team used a laser to burn into the film an array of pores of various sizes. When the temperature was raised to , some pores began to close, while some opened up. “Only one ‘magic’ hole doesn’t grow or shrink,” Dalnoki-Veress says. This pore corresponds to the critical radius, which the team measured precisely by switching to an atomic force microscope. Using films of different thicknesses, the researchers found that the critical radius was proportional to the thickness, as expected for this simple polymer.
In a second round of experiments, the researchers chose a more complex polymer whose molecules have a tendency to line up with each other, forming several layers. This structure mimics the lipid bilayers that make up many biological membranes. When the team burned pores in this polymer, they found that the critical radius reached a minimum value for a film thickness of about 300 nanometers. For films thinner than that, the critical radius became larger. To explain this behavior the team modeled the rim of the pore with a curved surface. They assumed that the bending of the surface disrupts the flat layers of the polymer molecules, forcing them to rearrange. By adding a bending resistance to the edge tension, the researchers’ model predicted a minimum critical radius, in agreement with the data. This theoretical explanation suggests an important effect of the high density of proteins found in cell membranes: the proteins alter the bending resistance, thereby reducing the membrane’s susceptibility to forming pores.
Fluid physicist Jacco Snoeijer from the University of Twente in the Netherlands says that this work consists of “really beautiful, delicate experiments.” In studies of pore formation, as well as crystal nucleation, “one often observes the macroscopic consequences after growth, while the microscopic nucleation events are in many cases difficult or impossible to assess directly,” he says. The team’s direct observation of the critical pore size provides insight into the nature of the edge tension, says Snoeijer.
This research is published in Physical Review Letters.
–Michael Schirber
Michael Schirber is a Corresponding Editor for Physics Magazine based in Lyon, France.