Extending an Alternative to Feynman Diagrams
Scattering amplitudes are the key ingredients for making theoretical predictions about what particle physics experiments will observe. Knowing them allows you to calculate the probability that interacting particles will scatter into a certain collection of particles. A team of theorists from the California Institute of Technology in Pasadena and Charles University in Prague (Cheung et al.) has now outlined how to extend a modern technique for calculating these amplitudes to a class of physical theories known as effective field theories [1]. Such theories are encountered in descriptions of pion interactions and in attempts to extend the standard model, and the work might lead to innovative approaches to solving problems in these areas. But the main interest in this technical advance is that it takes a step toward reformulating quantum field theories in a new way.
Quantum field theories provide the mathematical language in which to express ideas in many branches of modern physics. This language was first developed to address the needs of relativistic quantum mechanics, the domain of high-energy particle interactions. But it’s now also widely used in condensed-matter and statistical physics. Quantum field theories are the starting points for predicting what happens when two relativistic protons collide at a particle accelerator or for understanding the properties of so-called strongly correlated electron materials.
The fields in a quantum field theory represent quantum-mechanical operators that depend on spatial position and time. Each field carries additional quantum numbers for spin and other internal degrees of freedom. All particles—from photons and electrons to the Higgs boson and other fleeting particles produced at high-energy accelerators—are excitations of these fields. The same is true for the quasiparticles that arise in condensed-matter systems.
Thanks to Richard Feynman's deep insight, all observable quantities in a quantum field theory, such as scattering amplitudes, can be expressed using a so-called path integral over all possible classical field configurations. Each configuration is weighted by a pure phase, whose value depends on the spatial integral of the Lagrangian (a functional that describes the interactions between the fields) divided by Planck's constant. The path integral adds in the effects of quantum fluctuations, which depend on the distance (or energy) at which the field is probed. As we probe at shorter and shorter distances (higher and higher energies), we strip away quantum fluctuations.
There are various approaches to calculating the path integral. At strong coupling, the path integral can be put on a spacetime lattice and computed numerically. At weak coupling, path integrals lead to a perturbative expansion via Feynman diagrams. Feynman diagrams provide both a heuristic picture of the scattering amplitudes particle physicists want to calculate and a concrete formalism for doing the calculations. But they suffer from a key flaw in gauge theories, such as the standard model: the number of diagrams increases factorially with the number of external particles or the number of closed loops.
In some special cases, however, the result of summing over many diagrams can be extremely simple, as in the celebrated example of the Parke-Taylor formula, which describes the interaction between gluons [2, 3]. This simplicity led theorists to realize that there was an alternative approach to computing scattering amplitudes that avoids Feynman diagrams entirely. These approaches don’t start with the Lagrangian but, instead, from first principles. The simplest amplitude that can be calculated, and the starting point for calculations involving more particles, is the case of three gluons, the carriers of the strong force. One can start with only three basic ingredients—Lorentz invariance, locality, and a dimensionless coupling—and derive the amplitude for the three gluons [4]. It’s then possible to use this solution to find the scattering amplitudes for greater numbers of gluons by requiring that the new amplitudes “factorize” correctly, meaning they separate into products of simpler amplitudes (see note in Ref. [5]).
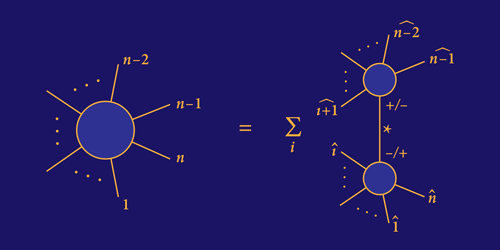
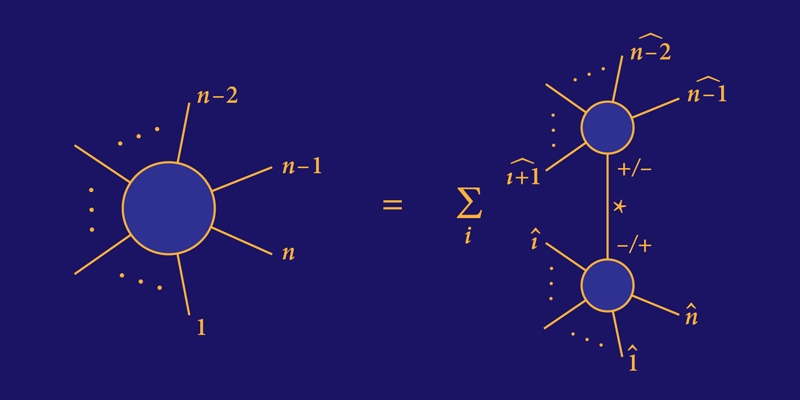
This requirement of factorization is, in general, the key to computing scattering amplitudes without the aid of Feynman diagrams. A decade ago, Ruth Britto, Freddy Cachazo, Bo Feng, and Edward Witten (BCFW) observed that one can use factorization to give a recursive expression [6] in terms of amplitudes with fewer external particles (similar to what is shown in Fig. 1). For example, one can express the interaction of four particles as a product of three-particle interactions. One just has to assume a mild condition on the behavior of the amplitudes, as some modified momenta become infinite while maintaining momentum conservation. This “infinite momentum” condition can be satisfied in a variety of theories and, in particular, in gauge theories. BCFW derived their recursion by using Cauchy's theorem, which allows the evaluation of certain integrals. This enabled them to relate the analytic behavior of the scattering amplitude to its behavior in certain “factorization channels,” the name given to the way in which a scattering amplitude is broken down into simpler amplitudes.
However, this simplifying approach hits a wall when it comes to tackling what are known as effective field theories. Unlike the standard model and other theories in its class, effective field theories contain additional terms, of higher engineering dimension, whose coefficients grow as the theory is probed at shorter distances (higher energy). More importantly, quantum corrections induce a tower of terms of yet higher dimension. These theories are dubbed “effective” because they are not valid at all distance scales—at some short distance, they cease to be valid and must be replaced by a simpler, underlying theory. A classic example is that of the Fermi description of the weak interactions, where a term containing four fermion fields, of engineering dimension six, ultimately gives way to the exchange of W bosons. Unfortunately, the infinite-momentum condition used by BCFW is typically not satisfied in effective field theories. It would seem as though one must revert to the arduous task of computing Feynman diagrams. Cheung et al., however, solve this problem for a particular class of effective field theories [1].
The problem with effective field theories that the authors address is that higher-dimension terms give rise to contributions that cannot be determined by factorization. In some effective field theories, however, these higher-dimension terms are connected to lower-dimension ones by symmetries. This is the case, for example, for nonlinear sigma models, which describe pion interactions at low energies. In this case, and in others, the symmetries are reflected in the behavior of the scattering amplitudes: they approach zero more rapidly as we take some of the external momenta to zero. Cheung et al. take advantage of this behavior to extend the applicability of Cauchy’s theorem to cases where the infinite-momentum condition fails to hold.
Their work allows us to extend the idea of defining quantum field theories via physical principles, instead of via a Lagrangian, to an important class of effective field theories. The ability to derive scattering amplitudes from physical principles may reveal deeper connections between different field theories, a task that would be difficult to do within the Lagrangian framework. The paper by Cheung et al. takes a step in this direction. In addition, the recursion relations for effective theories offer a compact form for computing amplitudes with, for example, many pions. They also connect nicely to recent work on novel representations of amplitudes [7–9].
Acknowledgment
D. A. Kosower acknowledges the support of the Ambrose Monell Foundation.
This research is published in Physical Review Letters.
References
- C. Cheung, K. Kampf, J. Novotny, C.-H. Shen, and J. Trnka, “On-Shell Recursion Relations for Effective Field Theories,” Phys. Rev. Lett. 116, 041601 (2016).
- S. J. Parke and T. R. Taylor, “An Amplitude for n-Gluon Scattering,” Phys. Rev. Lett. 56, 2459 (1986).
- M. L. Mangano and S. J. Parke, “Multi-Parton Amplitudes in Gauge Theories,” Phys. Rep. 200, 301 (1991).
- N. Arkani-Hamed, F. Cachazo, and J. Kaplan, “What is the Simplest Quantum Field Theory?,” J. High Energy Phys. 2010, No. 9, 16 (2010).
- More precisely, the requirement is that the amplitudes factorize when a sum of the external momenta approaches a zero-mass vector.
- R. Britto, F. Cachazo, B. Feng, and E. Witten, “Direct Proof of the Tree-Level Scattering Amplitude Recursion Relation in Yang-Mills Theory,” Phys. Rev. Lett. 94, 181602 (2005).
- F. Cachazo, S. He, and E. Y. Yuan, “Scattering of Massless Particles in Arbitrary Dimensions,” Phys. Rev. Lett. 113, 171601 (2014).
- F. Cachazo, S. He, and E. Y. Yuan, “Scattering Equations and Matrices: from Einstein to Yang-Mills, DBI and NLSM,” J. High Energy Phys. 2015, No. 7, 149 (2015).
- N. Arkani-Hamed and J. Trnka, “The Amplituhedron,” J. High Energy Phys. 2014, No. 10, 030 (2014).