Unexpected Twins
A crystal stressed beyond its elastic limit will undergo plastic deformation, which results in an irreversible change of shape. Such a deformation occurs through two primary mechanisms: twinning, in which one part of the crystal shears with respect to the other along a preferred plane; and slip, a slower and more chaotic process where multiple atomic planes slide over one another. Researchers often rely on a system of simple rules to predict in which of these two ways (or others) a particular material will deform. For instance, aluminum is thought to deform primarily by slipping, while titanium by twinning. However, deformation is a complex process, and the favored mechanism for a given crystal depends not only on its microstructure but also on the way in which an external force (or “load”) is applied. Feng Zhao at the Peac Institute of Multiscale Sciences, China, and colleagues have now shown that a single crystal of aluminum—a material that in most circumstances would deform by slipping—can exhibit a significant degree of twinning. This unexpected behavior was observed when the metal was forced to deform dynamically in a complex geometric environment [1]. Results like the ones reported by Zhao et al. suggest that we need to review our understanding of how crystalline materials deform [2].
A material can deform via a range of competing mechanisms. The material’s strength—its capacity to withstand an applied load without deforming or fracturing—is thus determined by which deformation mechanisms can operate as force is applied. Both twinning and slip start from defects—disordered regions or boundaries between different crystalline grains. At atomic scales, the strength of a solid is dictated by the interactions of valence electrons. If the loaded volume contains only a small number of perfectly packed atoms, its strength has its maximum possible value, which is determined by the strength of the chemical bonds. In larger volumes, however, strength depends on a combination of forces that includes electrostatic bonds and mechanical joints but also the presence of defects. Thus, as more interfaces are included, strength declines because more routes to failure exist.
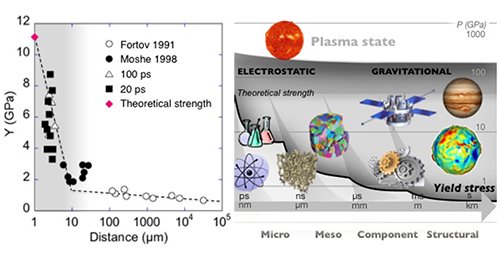
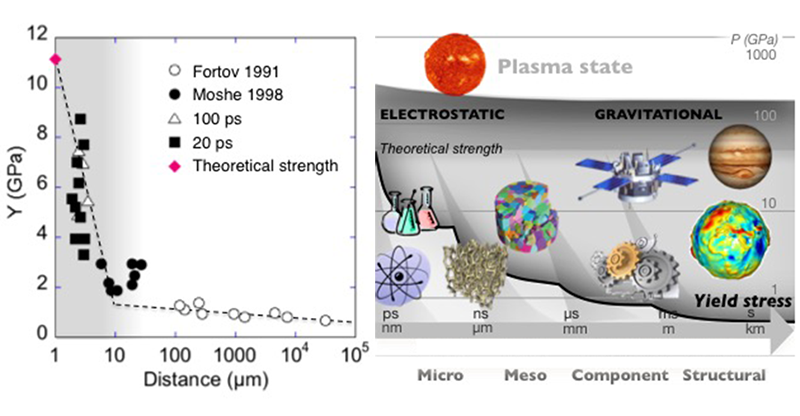
These complexities mean that the strength of matter has no single, universal value. Figure 1 (left) shows the decline in the tensile strength of aluminum as a function of the duration of the pulse that is applying a stress (different pulse duration regimes can be obtained with lasers, guns, and static presses) [3–5]. Since a compression front deforms the material until the end of a pulse completes the loading, longer pulses sweep deeper into the microstructure, sampling larger volumes that contain more defects and reducing the apparent strength of the metal. As the structures become larger, strength is controlled less by electrostatic forces and more by gravitational ones. This is the same reason that planets evolve to be spherical with the densest elements at their core [Fig. 1 (right)] [5].
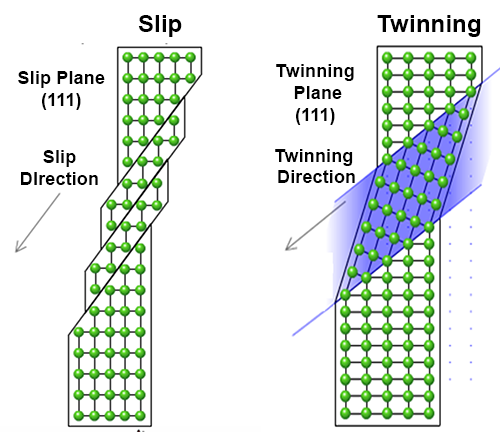
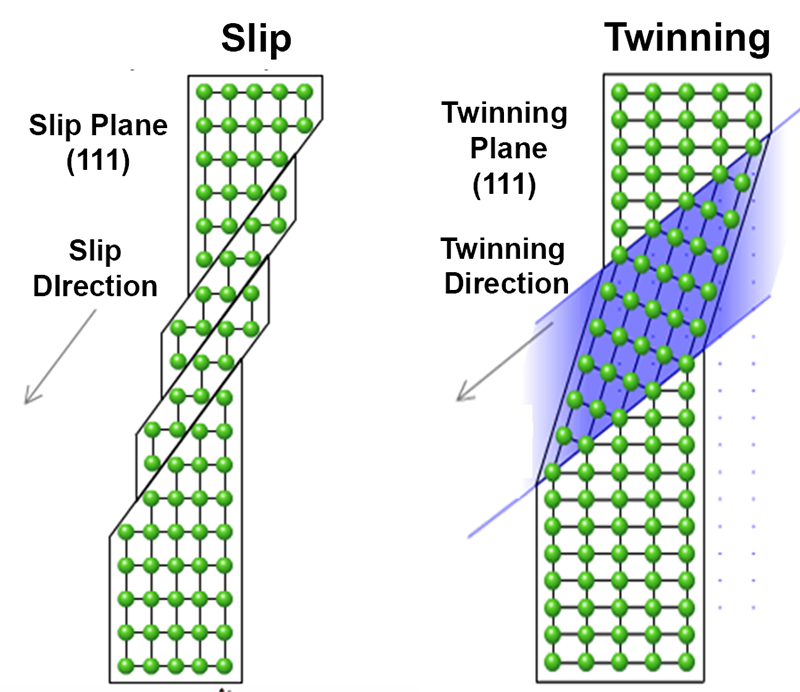
A cartoon of slip and twinning deformations is shown in Fig. 2. Slip is generally more likely than twinning in metals (and certainly in aluminum), but the reverse is true when atomic structure becomes more complex. Importantly, moving a slice of a crystal (as in slipping) takes much longer than shifting the positions of atoms (as in twinning). In both cases deformation starts from some preexisting defects and the processes that initiate it are not entirely understood. Under the right conditions, for instance under very high strain rates, twins may propagate immediately across a single crystalline grain. For this reason twinning is often thought to only occur beyond a “threshold stress” or “twinning pressure.”
But evidence is mounting that there is no single criterion for twinning, as the work of Zhao et al. now shows. The authors have found that single-crystal aluminum (which preferentially slips) starts to twin when the material is compressed and sheared to a point that it forms new grains and (at much larger scales) even shear bands to accommodate the flow. Similarly, other studies have shown that titanium (which preferentially twins) starts to slip when it has a nanograined structure [6]. These counterintuitive observations illustrate the need to review our rules of thumb for the deformation of materials.
In their experiments, the researchers pressed a single-crystal aluminum rod into a T-shaped duct, which extruded the incoming rod into the two 90° bends at the top of the T. This results in complex deformation dynamics within the rod, resulting from high compression, tension, shear in the duct, and friction between the rod and the duct walls. In such a process, the rod underwent a huge strain—about 200%—an amount that can only be achieved by a combination of twinning, slip, and even the formation of shear bands at the mesoscale under the steep gradients of strain rate, velocity, and temperature imposed in the experiments.
The authors used molecular dynamics simulations to provide “movies” of the atomic dynamics that might have occurred in their experiments. The simulations suggest that both slip dislocations and twinning can be nucleated at defects and propagate at the atomic scale. In particular, under the experimental conditions, the estimated shear stress can reach values that are sufficient to initiate deformation twinning. The picture emerging from the simulations was confirmed by experiments. The researchers recovered the cooled fragments and analyzed them with electron microscopy. Images of the samples show mesoscale shear-band features similar to those obtained in the atomic simulations, illustrating that deformation structures evolve from atomic to macroscopic scales as the crystalline material flows. Together, experiments and simulation allowed the authors to conclude that slip and twinning can act together as complementary deformation modes.
If we are to revise our perceptions of crystalline flow in a material, we need to devise new experiments and theories that tackle all of the critical factors that determine slip or twinning. These include the temperature and pressure around a target, the size of the crystalline zone, the magnitude of the stress applied, and the strain rate at which it is delivered. For each microstructural element, the geometry of the crystal and its mechanical state will favor slip or twinning. Once either process starts, the resulting local conditions will close the door to the other until deformation nucleates again at the next defect.
Zhao and co-workers have illustrated that matter can use a wider range of ways to flow than had previously been recognized. This should encourage us to revise the concept that strength has a fixed value, constant over time. It should rather be thought of as a transient, local property of matter, dictated by all the deformation mechanisms available in a certain configuration. To tackle the complexity of these problems, researchers will need to deploy new imaging methods that can probe atomic, meso-, and macroscales. They should also develop suitable techniques for processing the big data generated in experiments and simulations. Moreover, if we can marry the efforts of physics, materials sciences, and engineering, we might be able to construct a wider picture of phenomena that, so far, no individual field has been able to explain.
This research is published in Physical Review Letters.
References
- F. Zhao et al., “Macrodeformation Twins in Single-Crystal Aluminum,” Phys. Rev. Lett. 116, 075501 (2016).
- N. Bourne, “Shock and Awe,” Physics World 22, No. 01, 26 (2009).
- E. Moshe, S. Eliezer, E. Dekel, A. Ludmirsky, Z. Henis, M. Werdiger, I. B. Goldberg, N. Eliaz, and D. Eliezer, “An Increase of the Spall Strength in Aluminum, Copper and Metglas at Strain Rates Larger than 107 s−1,” J. Appl. Phys. 83, 4004 (1998).
- B. A. Remington et al., “Materials Science under Extreme Conditions of Pressure and Strain Rate,” Metall. Mater. Trans. A 35, 2587 (2004).
- N. Bourne, Materials in Mechanical Extremes: Fundamentals and Applications (Cambridge University Press, Cambridge, 2013)[Amazon][WorldCat].
- Q. Yu, Z.-W. Shan, J. Li, X. Huang, L. Xiao, J. Sun, and E. Ma, “Strong Crystal Size Effect on Deformation Twinning,” Nature 463, 335 (2010).