A New Twist in Simulating Solar Flares
Protecting humans and their technologies from the harmful effects of space weather is nothing new. Yet a recent event demonstrated how fateful such events can be. On November 4, 2015, an active region on the Sun known as NOAA 12443 unleashed a flare—a gust of high-speed charged particles—whose radiation deactivated the radars at Sweden’s airports, grounding all of the country’s commercial flights. Such events underscore our need to be able to predict when the next solar flare will occur and how much energy it might release. This longstanding goal of astrophysics will rely heavily on numerical simulations. Now, Piyali Chatterjee of the University of Oslo, Norway, and her collaborators have taken a significant step towards improving such simulations by developing the first numerical model that explains how magnetic fields from deep below the Sun’s surface can produce energetic flares in the corona [1]. Researchers have assumed that this was the mechanism for flares, but it has been difficult to demonstrate with simulations. Chatterjee et al. do so by making very simple, yet physically realistic, assumptions.
Solar flares occur when giant “tubes” of magnetic flux in the Sun’s outer envelope, or corona, become unstable, releasing their stored energy in an explosive burst. The magnitude of this energy is around , which is roughly equivalent to the energy delivered by the impact of a 10-km-wide asteroid, such as the one causing the mass extinction on Earth, 66 million years ago. Only a fraction of the flare’s energy strikes the Earth, but it can be enough to destroy electronics and is a potential health risk to those who travel frequently by air, particularly near the Arctic.
Although solar flares occur in the corona, the tubes of flux that give rise to solar flares originate from the movement of ions and electrons in the Sun’s interior. In fact, it is widely believed that the tubes form deep within the Sun, up to 200,000 km below its surface (the bottom of the convection zone). What’s unclear is how they are able to pass through the Sun’s turbulent interior and to its surface with enough energy density left to produce a flare. One postulate is that the tubes survive the ascent if their field lines twist around like the strands in a braid. This twist provides an inward force that opposes the expansion of the axial field during the tube’s ascent.
So far, twist has been treated as a free parameter in simulations. Chatterjee et al. show that it can emerge naturally in simulations that incorporate the Sun’s rotation. When a flux tube forms, the pressure associated with its field displaces (or dilutes) plasma. This makes the region within the tube lighter than its surroundings, giving rise to an upwards force—an effect known as magnetic buoyancy. As the tube rises, the trajectories of its constituent ions “swerve” because of the Sun’s rotation (the Coriolis effect), causing the field lines to become twisted.
The researchers have recreated this process in their simulations. They start with a sheet of magnetized plasma that lies about 8000 km below the Sun’s surface and has a field strength (parallel to the sheet) of 20,000 G. After 30 min of solar time, the sheet breaks into (energetically more favorable) separated tubes of flux, which become highly twisted by the Sun’s rotation by the time they reach the corona. The authors show that flares, with energies of to , occur at localized sites where magnetic energy is converted into kinetic energy and eventually into heat (see Fig. 1). These events are associated with magnetic reconnection, where field lines of opposite polarity break and reconnect. Chatterjee et al. also show that these flares can occur multiple times when segments of the coronal field suddenly become “overtwisted” and release energy.
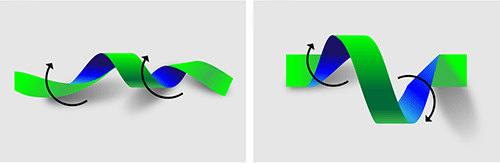
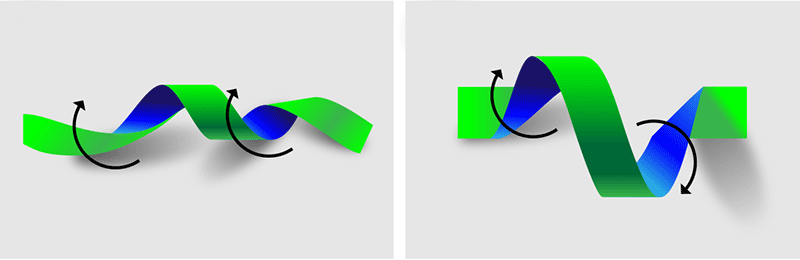
Up to now, simulations have initialized twist in an ad hoc and unrealistic way; specifically, the twist only wound in one sense (like a spiral staircase), as in the left side of Fig. 2. However, in Chatterjee et al.’s simulations, when a twist that winds in one sense appears, it is always accompanied by a counterwinding twist, as in the right side of Fig. 2. This conserves what is known as the magnetic helicity, which is a measure of twist integrated over volume. And it may be the factor that helps the reconnection process associated with a flare, because it increases the chance that a twisted field will be surrounded by an oppositely wound field, allowing the two to easily reconnect.
Several groups have simulated the emergence of magnetic fields from below the convection zone into the corona. But in many of these simulations, the magnetic fields were untwisted. Most of the flux therefore “accumulated” just beneath the surface without actually penetrating it [2], so no flares were produced. But a twisted magnetic field, like that emerging in Chatterjee et al.’s simulations, wants to untwist. It can do so much more easily once it is close to the surface, where the surrounding pressure is smaller [3].
The advantage of the authors’ approach is that the emergence of twist is anchored in a physical phenomenon—the Sun’s rotation. However, the time it takes a flux tube to rise to the surface because of magnetic buoyancy is only a few hours, which is short compared with the Sun’s rotation period of 25 days. One can therefore reasonably ask: How could sufficient twist be generated in such a short time? The answer might be that the Sun is highly stratified—the density of plasma and its pressure change rapidly while moving from the center to the surface. Rising plasma therefore expands rapidly over a short distance, and since the Coriolis effect on the plasma depends on the amount of expansion, this enhances the effect of the Sun’s rotation.
The simulations provide an estimate of the maximum flare energy that the Sun, or another star, could potentially produce. Chatterjee et al. find that their model predicts flares with energies as high at , but the Kepler spacecraft has detected many so-called superflares—flares producing energies above —from stars like our Sun [4]. Since there is no tight correlation between flare frequency and stellar rotation rate [5], superflares might be possible even for the relatively slowly rotating Sun [6]. The consequences of superflares for people and their technologies on the Sun-facing side of the Earth are extreme, and future simulations based on Chatterjee et al.’s model might now be able to put realistic limits on just how bad a worst-case scenario could be.
Acknowledgments
A. Brandenburg acknowledges partial support from the Swedish Research Council grant 2012-5797 and the FRINATEK grant 231444 under the Research Council of Norway.
References
- P. Chatterjee, V. Hansteen, and M. Carlsson, “Modeling Repeatedly Flaring Sunspots,” Phys. Rev. Lett. 116, 101101 (2015).
- P. Syntelis, V. Archontis, C. Gontikakis, and K. Tsinganos, “Emergence of Non-Twisted Magnetic Fields in the Sun: Jets and Atmospheric Response,” Astron. Astrophys. 584, A10 (2015).
- J. Warnecke, A. Brandenburg, and D. Mitra, “Magnetic Twist: A Source and Property of Space Weather,” J. Space Weather Space Clim. 2, A11 (2012).
- H. Maehara, T. Shibayama, S. Notsu, Y. Notsu, T. Nagao, S. Kusaba, S. Honda, D. Nogami, and K. Shibata, “Superflares on Solar-Type Stars,” Nature 485, 478 (2012).
- S. Candelaresi, A. Hillier, H. Maehara, A. Brandenburg, and K. Shibata, “Superflare Occurrence and Energies on G-, K-, and M-type Dwarfs,” Astrophys. J. 792, 67 (2014).
- K. Shibata et al., “Can Superflares Occur on Our Sun?,” Publ. Astron. Soc. Jpn 65, 49 (2013).