A Close Look at the Fermi-Hubbard Model
Understanding how large assemblages of interacting particles behave at low temperatures can be a difficult business. Often, new phenomena are first observed in complicated settings, long before predictive models of the phenomena are identified. Engineering a clean realization of these models of many-body physics in the laboratory can offer a model system with inherent simplicity. In a new study [1], Michael Köhl from the University of Bonn, Germany, and colleagues have done just this, producing detailed images of an atomic gas described by the 2D Fermi-Hubbard model—the simplest model of interacting fermionic particles in a 2D lattice. The researchers present a type of precision test of the model’s equation of state, in a cold-atom setting that we are sure conforms accurately to the model. The test adds an important case to the growing number of precision laboratory tests of simple many-body model systems that have been interrogated in the controlled setting of cold-atom physics.
Even the simplest models of many-body phenomena often present too many riches to contemplate simultaneously. This is perhaps the situation for the case of interacting fermionic particles hopping in the periodic potential defined by a 2D lattice. To begin with, at very low temperatures, the particles do something truly magical. If their density is close enough to commensurate with the periodic potential, with approximately an integer average number of particles per lattice site, they will spontaneously choose to localize. The gas enters an incompressible state called the Mott phase and behaves as an insulator rather than a metal [2]. The simplest model of such behavior, the Fermi-Hubbard model, includes only hopping between adjacent sites and only considers interactions between particles that are on the same site. Localization is just the starting point of this model. With the balance and organization of particle spins still undefined, room is left in the model’s ground-state phase diagram for several phenomena—antiferromagnetism, incommensurate spin order, d-wave pairing, density waves, pseudogap phases, and perhaps more. We have known the phenomenon of localization since Nevill Mott and Rudolf Peierls outlined it in the late 1930s, and Martin Gutzwiller, John Hubbard, and Junjiro Kanamory devised the Fermi-Hubbard model in the early 1960s. Since this time, the Fermi-Hubbard model has become the basis for much of what we know about superfluidity in periodic systems, quantum magnetism, and strongly correlated fermion physics on lattices in general.
Köhl and co-workers present an impressive characterization of the ground-state phase diagram of the 2D Fermi-Hubbard model. The authors created a 2D Fermi gas of neutral potassium-40 atoms that hop between the sites of an optical lattice potential formed by interfering laser beams. Placing the gas within close proximity of a high-resolution imaging apparatus, they were able to image the full density profile of the system in situ, separating singly and doubly occupied sites using a clever trick of radio-frequency spectroscopy. This approach allowed them to capture the behavior of the gas over a wide range of temperatures and particle-interaction strengths, from noninteracting to strongly interacting.
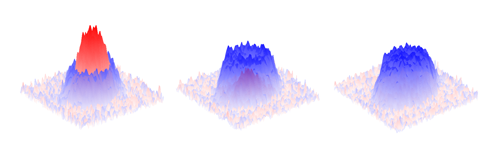
This is not the only recent study to directly image fermionic lattice gases [3], or their bosonic cousins [4], in the insulator regime. But several features set this work apart from other studies. First, the experiment probed a sufficiently large 2D sample to obtain the system’s equation of state from the imaged density profile and the known spatial variation of the lattice potential. Second, the authors carried out a detailed comparison between their data and theory, in the form of computational techniques using numerical linked cluster expansions (NLCE) [5] and dynamical cluster approximations (DCA) [6]. The emergence of a Mott insulator is seen clearly from the measured density (Fig. 1), and the compressibility extrapolates well from the noninteracting metallic limit to the values predicted by DCA deep in the insulator limit. Producing such experimental data is not an easy task: although the technology for creating cold quantum gases is by now mature, arranging for this to happen in a 2D Fermi-Hubbard system near thermodynamic equilibrium is difficult. Maintaining and characterizing near-thermodynamic equilibrium conditions over such wide parameter ranges, and obtaining reliable direct images, require conscientious effort and new tricks.
Understanding phase diagrams of simple model systems precisely is about far more than testing well-established theory, and the 2D Fermi-Hubbard model is perhaps the best illustration of this point. A few decades after it was introduced, the model took on a new significance in the search for the cause of high-temperature superconductivity in copper-oxide compounds. Philip W. Anderson proposed a theory [7] to describe the effect—called the resonating valence bond theory—that is built on the 2D Fermi-Hubbard model. Years later, the Fermi-Hubbard phase diagram was revisited through the lens of quantum criticality, and new interpretations of its structure were offered by the presence of an underlying phase transition. The fact that new insights into the “plain vanilla” Fermi-Hubbard model continued to be uncovered for decades after its introduction, and to this day, is testament to the fact that profound discoveries can lay dormant in seemingly simple quantum systems. It also reminds us that, even in an era of targeted experimentation and daunting theoretical prowess enhanced by large-scale computing, many-body physics is still a humbling natural science based on discovery.
“Trolling” for phase changes via precise experimental extraction of the equation of state makes sense, and Köhl and colleagues give us a taste for this in their study. They provide density measurements precisely at the ratio between the scales of particle interaction and kinetic energy at which antiferromagnetic ordering (recently seen more directly [8]) would persist to the highest temperatures.
There is good reason for studies of Fermi-Hubbard thermodynamics to continue, particularly in two dimensions, at increasingly higher precision, and with close adherence to the simple models prescribed by Hubbard, Mott, and others. The ability to build “precisely simple” model systems and scrutinize them closely is the only way to tease out the essential building blocks of complex many-body behavior.
This research is published in Physical Review Letters.
References
- E. Cocchi, L. A. Miller, J. H. Drewes, M. Koschorreck, D. Pertot, F. Brennecke, and M. Köhl, “Equation of State of the Two-Dimensional Hubbard Model,” Phys. Rev. Lett. 116, 175301 (2016).
- R. Jördens, N. Strohmaier, K. Günter, H. Moritz, and T. Esslinger, “A Mott Insulator of Fermionic Atoms in an Optical Lattice,” Nature 455, , 204 (2008); U. Schneider, L. Hackermuller, S. Will, Th. Best, I. Bloch, T. A. Costi, R. W. Helmes, D. Rasch, and A. Rosch, “Metallic and Insulating Phases of Repulsively Interacting Fermions in a 3D Optical Lattice,” Science 322, 1520 (2008).
- D. Greif, M. F. Parsons, A. Mazurenko, C. S. Chiu, S. Blatt, F. Huber, G. Ji, and M. Greiner, “Site-Resolved Imaging of a Fermionic Mott Insulator,” Science 351, 953 (2016); C. Hofrichter, L. Riegger, F. Scazza, M. Höfer, D. R. Fernandes, I. Bloch, and S. Fölling, “Direct Probing of the Mott Crossover in the SU(N) Fermi-Hubbard Model,” arXiv:1511.07287.
- See, e.g., N. Gemelke, X. Zhang, C.-L. Hung, and C. Chin, “In Situ Observation of Incompressible Mott-Insulating Domains in Ultracold Atomic Gases,” Nature 460, 995 (2009); W. S. Bakr, A. Peng, M. E. Tai, R. Ma, J. Simon, J. I. Gillen, S. Folling, L. Pollet, and M. Greiner, “Probing the Superfluid-to-Mott Insulator Transition at the Single-Atom Level,” Science 329, 547 (2010).
- E. Khatami and M. Rigol, “Thermodynamics of Strongly Interacting Fermions in Two-Dimensional Optical Lattices,” Phys. Rev. A 84, 053611 (2011).
- J. P. F. LeBlanc and E. Gull, “Equation of State of the Fermionic Two-Dimensional Hubbard Model,” Phys. Rev. B 88, 155108 (2013).
- P. W. Anderson, “The Resonating Valence Bond State in La2CuO4 and Superconductivity,” Science 235, 1196 (1987).
- R. A. Hart, P. M. Duarte, T.-L. Yang, X. Liu, T. Paiva, E. Khatami, R. T. Scalettar, N. Trivedi, D. A. Huse, and R. G. Hulet, “Observation of Antiferromagnetic Correlations in the Hubbard Model with Ultracold Atoms,” Nature 519, 211 (2015).