Black Holes Produce Complexity Fastest
Black holes hold an impressive number of world records, both observational and theoretical. In astrophysics, they are believed to be the densest objects and to power the most luminous sources. In the theoretical realm, black holes push the extremes of gravitation and quantum mechanics and in several cases actually set fundamental limits—on density, entropy, and a growing list of other attributes—for quantum systems. Adam Brown and colleagues at Stanford University, California, and the Massachusetts Institute of Technology, Cambridge [1], now argue that we should add a new world record to the list: computational complexity.
Computational complexity in a gravitational theory, in which degrees of freedom are continuous rather than discrete, is easy to describe but difficult to define. The authors propose a simple and precise formula, show that it passes a number of nontrivial checks, and find an intriguing connection to black hole dynamics. This leads them to conjecture that black holes produce complexity at the fastest possible rate allowed by physical laws.
Complexity has two facets, information storage and information processing, or in computing terms, memory and speed. In the 1970s, Jacob Bekenstein [2] showed that black holes set a theoretical maximum on information storage, which applies to any quantum computer or, indeed, any physical system governed by quantum mechanics. Bekenstein argued that no object can have more entropy than a black hole of the same size. Entropy counts quantum states, and storing more bits of information requires more states, so an upper limit on entropy is also an upper limit on information storage. Bekenstein’s entropy bound is therefore a fundamental limit, imposed by thermodynamics, on the memory capacity of any quantum computer, independent of technological details.
So memory is bounded, but what about speed? The rate of computation also obeys ultimate physical limits. A theorem of Norman Margolus and Lev Levitin states that in one second, a quantum system of average energy E can evolve through, at most, 2E∕𝜋ℏ distinct states, where ℏ is the reduced Planck constant. In computing language, this is a theoretical upper limit on the number of operations that can be performed in a second [3].
Brown et al. [1] discovered a surprising connection between this rate limit and black hole dynamics (see also Ref. [4] for detailed calculations of the results). In an attempt to define the computational complexity of a black hole, they studied the gravitational action of a black hole spacetime. The gravitational action, introduced by Albert Einstein and David Hilbert, is a thoroughly studied quantity that describes the dynamics of the gravitational field. The insight of the present work was to define the action not for the entire spacetime but for a subregion that corresponds roughly to the black hole interior. This was motivated by the intuition that the quantum state of a black hole is somehow encoded in its interior geometry. After a somewhat lengthy and technical calculation, they found that the action of the interior increases at a rate exactly equal to the Margolus–Levitin bound, 2E∕𝜋ℏ. This led them to conclude that action plays the role of complexity in quantum gravity, and that black holes produce complexity at the fastest possible rate.
The importance of black holes in setting physical limits on computing was also discussed by Seth Lloyd [5]. Lloyd invoked Bekenstein’s black hole argument to bound the memory and the Margolus–Levitin theorem to bound the speed. The new surprise that emerges from Brown and colleagues’ study is that, apparently, both bounds are attained by black holes: the bound on memory is set by the thermodynamics of black holes in equilibrium, and the bound on speed is set by the dynamics of black hole interiors. Although the limits are phrased in computing language, a black hole is certainly not a computer in the usual sense—it cannot, as far as we know, be controlled in order to run algorithms or surf the web. However, the bounds apply to any physical system, whether it is a quantum computer, an ordinary laptop, or a natural object like a black hole, since all of these are ultimately governed by quantum mechanics.
Interestingly, the black hole calculations that underlie these bounds are performed using classical general relativity, but the results are interpreted as limits on the memory and speed of quantum systems. This quantum/classical duality began with the work of Bekenstein and developed eventually into a relationship known as the anti-de Sitter/conformal field theory (AdS/CFT) correspondence—an exact mapping between theories of gravity and quantum fields. The recent work of Brown et al. was inspired by the fact that, in this mapping, classical geometries in general relativity encode information-theoretic properties of the dual quantum system [6, 7].
Within the duality, black holes represent quantum states with high energy density. From the outside, they appear to be static, but this is an illusion—the same illusion that makes typical high-energy states almost indistinguishable from thermal states. The inside of a black hole, inaccessible to outside observers, tells a different story [8]. It expands with time, and this expansion translates into a growth in quantum entanglement, quantified by entanglement entropy.
Entanglement entropy is a measure of “quantumness” that vanishes for classical states, and it is large when quantum correlations are important. It is also a measure of complexity. This has practical consequences for numerical calculations of quantum systems, for example using the density matrix renormalization group (DMRG) technique: States with low entanglement entropy can be efficiently simulated on a classical computer but highly entangled states cannot. At high energy density, even simple initial states quickly evolve into highly entangled, very complex states, nearly impossible to simulate. In the dual geometric picture of AdS/CFT, the exponential growth in computing power needed to simulate late-time dynamics of high-energy states [9] is a numerical “discovery” of the growing black hole interior.
However, this raises a puzzle. Entanglement entropy grows at early times, but quickly saturates at its equilibrium value. Black hole interiors, on the other hand, grow for an exponentially long time. Leonard Susskind, a co-author of the new study, proposed that the continued growth in the interior reflects growing complexity of the quantum state, beyond the complexity captured by entanglement entropy [10]. This is what led Brown et al. to interpret the action of the black hole interior as a measure of complexity.
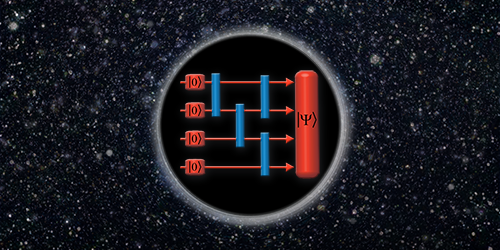
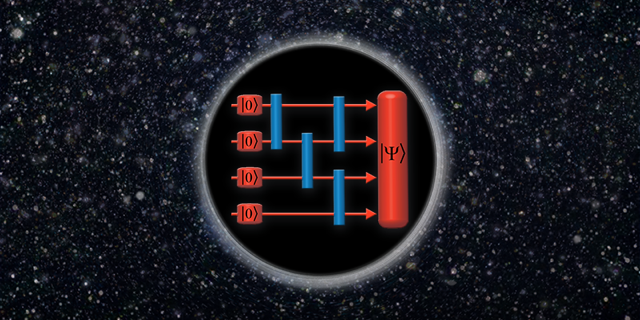
The definition of complexity in this context is unclear. In a discrete quantum system, such as N qubits, the complexity can be defined as the number of simple quantum gates required to construct the state of the qubits from a fixed reference state (say, the vacuum state). This defines the “circuit complexity” illustrated in Fig. 1. Brown and colleagues argue that the action of the interior should be interpreted as a continuum version of circuit complexity. This is speculative but suggests a starting point to find a suitable definition of circuit complexity in continuum quantum systems and hints at a fundamental role for complexity in understanding quantum gravity.
This research is published in Physical Review Letters.
References
- A. R. Brown, D. A. Roberts, L. Susskind, B. Swingle, and Y. Zhao, “Holographic Complexity Equals Bulk Action?,” Phys. Rev. Lett. 116, 191301 (2016).
- J. D. Bekenstein, “Black Holes and Entropy,” Phys. Rev. D 7, 2333 (1973).
- N. Margolus and L. B. Levitin, “The Maximum Speed of Dynamical Evolution,” Physica D 120, 188 (1998).
- A. R. Brown, D. A. Roberts, L. Susskind, B. Swingle, and Y. Zhao, “Complexity, Action, and Black Holes,” Phys. Rev. D 93, 086006 (2016).
- S. Lloyd, “Ultimate Physical Limits to Computation,” Nature 406, 1047 (2000).
- S. Ryu and T. Takayanagi, “Holographic Derivation of Entanglement Entropy from the anti–de Sitter Space/Conformal Field Theory Correspondence,” Phys. Rev. Lett. 96, 181602 (2006).
- Juan Maldacena, “Eternal Black Holes in anti-de Sitter,” J. High Energy Phys. 2003, No. 04, 021 (2003); M. Van Raamsdonk, “Building up Spacetime with Quantum Entanglement,” Gen. Rel. Grav. 42, 2323 (2010).
- T. Hartman and J. Maldacena, “Time Evolution of Entanglement Entropy from Black Hole Interiors,” J. High Energy Phys. 2013, No. 05, 014 (2013).
- T. Barthel, U. Schollwöck, and S. R. White, “Spectral Functions in One-Dimensional Quantum Systems at Finite Temperature Using the Density Matrix Renormalization Group,” Phys. Rev. B 79, 245101 (2009).
- L. Susskind, “Entanglement is Not Enough,” arXiv:1411.0690.