Measuring Quantum Kicks from a Beam of Light

Amir Safavi-Naeini

Viewpoint

Measuring Quantum Kicks from a Beam of Light

348 Via Pueblo Mall, Stanford University, Stanford, CA 94305-4088, USA

June 13, 2016• Physics 9, 64

Force sensors levitated by light have reached the quantum regime, in which their sensitivity is limited by the momentum kicks of individual photons.

Figure caption — **Figure 1:** A nanosphere (orange) levitated by a narrow-waisted optical field (blue) can act as a sensitive force sensor. Normally, the force noise from individual photons scattering from the sphere is too small to affect the sensor’s sensitivity: the kicks correspond to energies that are much smaller than the motional energy of the sphere (see diagram at right). But by stripping away the dominant noise sources—collisions with gas atoms in the trap— Novotny and colleagues were able to measure the miniscule amount of heating from photon kicks.

LIGO’s historic detection of gravitational waves using a laser interferometer [1] is a reminder of just how far scientists have come in their quest to use laser light to sense small forces. A continuing challenge is to improve the sensitivity of optics-based force detectors by eliminating the sources of noise that obscure the signals they’re designed to detect. A team led by Lukas Novotny from the Swiss Federal Institute of Technology (ETH), Zurich, reports progress along these lines by demonstrating an optically levitated nanosphere whose sensitivity to an external force is almost entirely limited by the background of momentum kicks it receives from individual photons [2]. This is a key step in developing force sensors that could eventually be used to study the quantum mechanics of macroscopic objects.

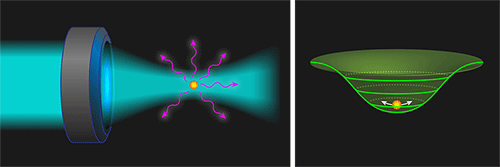
Nearly four decades ago, Art Ashkin pioneered the trapping and levitation of particles with light [3]. The technique takes advantage of radiation pressure to capture a dielectric particle, such as a glass bead, in the center of a tightly focused laser beam, which acts as a harmonic potential (Fig. 1). If an external force is applied to the particle, its position will shift from the center of the trap. Since this new position can be determined with high precision by measuring the phase of a laser that has interacted with the particle, optically levitated particles make excellent forces sensors. They have, for example, been used to detect forces as small as a few zeptonewtons [4].

Since they are not tethered to the outside world by any materials, optically levitated force sensors aren’t susceptible to the lattice vibrations and clamping losses that plague mechanical force sensors, such as cantilevers, tethered mirrors, or mechanically compliant membranes. However, optical sensors are prone to other noise sources. The most frequently observed, though arguably the least interesting, noise source is the dissipation and heating caused by the collision of gas molecules with the dielectric particle. These collisions impart tiny momentum kicks to the particle, producing background noise that is proportional to the pressure in the trapping chamber [3–7].

The experiment by the ETH group is the first to achieve low enough pressures for a noise source of purely quantum-mechanical origin to become dominant [2]. That source is photon-recoil heating, and it occurs because photons in the trapping field of the laser perform a sort of “Heisenberg’s microscope” experiment on the trapped nanosphere. Each time a photon is Rayleigh scattered by the nanosphere, it imparts a momentum kick to the particle. This recoil causes the particle’s energy to change by an amount of order of $ℏ^{2} k^{2} ∕ 2 m$ , where $k$ is the photon’s wavenumber, $m$ is the particle’s mass, and $ℏ$ is the reduced Planck’s constant. But in the ETH team’s experiment, this recoil energy is nearly ten billion times smaller than the amount of energy needed to excite one quantum of the nanospheres’s motion within the optical trap.

An alternative way to understand the miniscule effect of a single photon is to consider how much information about the trapped particle can be extracted from the scattered photon. For the experimental parameters chosen by Novotny’s group, the nanosphere’s zero-point fluctuation length is approximately 10 pm. This is the length scale on which a photon must measure the particle’s position in order to discern quantum fluctuations. However, the photons from the trapping laser have a wavelength of 1 $𝜇$ m, which is one hundred thousand times larger than the fluctuation length. As such, a scattered photon cannot perform a “strong” measurement of the particle’s position. In other words, the quantum backaction from the scattering of a single photon can have only a minor effect on the dynamics of the particle.

However, the cumulative momentum kicks from many scattering events can change the state of the nanosphere. The time scale needed for such a change is determined by the recoil-heating rate, which depends on the photon-scattering rate and the effect of each scattering event. The achievement of Novotny's group has been to measure the recoil-heating rate for an object as large as a 50-nm-diameter nanosphere.

For this measurement to succeed, the team had to reduce the motional energy of the sphere to an extremely low level, corresponding to an occupancy of 60 phonons in the harmonic trap, or a temperature of a few hundred microkelvins. Such cooling is typically accomplished by applying radiation pressure from a laser field along three orthogonal positions in the trap independently. In contrast, the ETH team utilized a parametric cooling process. This involves reading out the particle’s motion in each direction and then modulating the intensity of the trapping laser so as to adjust a parameter (in this case, the natural frequency of the harmonic trap) that deamplifies the particle’s motion [8]. The process is a bit like standing on a swing to decrease its amplitude.

Under optimal conditions, the researchers obtained a balance between cooling from the lasers and heating from noise that leads to an equilibrium temperature of about 500 $𝜇$ K. This final temperature has a linear dependence on pressure from $1 0^{- 6}$ to $1 0^{- 2}$ mbar, the range of trap pressures in which molecular collisions constitute the dominant noise source. However, at pressures below $1 0^{- 6}$ mbar the equilibrium temperature ceases to depend on the pressure. This is the regime in which photon recoil is the dominant source of heating and force noise. To measure the photon-recoil heating rate, the ETH group turned off their mechanism for cooling the particle by holding the laser intensity constant and allowing the particle to heat up through its interaction with the (room-temperature) environment. They then measured the rate at which this warm-up occurred, over many runs and at ultralow pressures, and determined that its value was on the order of a few tens of kilohertz—an impressively slow rate for a room-temperature experiment. In addition, the measured values of the photon-recoil heating rate for various experimental parameters agree with quantum predictions.

Since the first proposals for using trapped nanoparticles in quantum optical and optomechanical experiments [9, 10], major efforts have been directed at using these systems to observe quantum phenomena. Such sensors might allow us to someday test quantum mechanics itself in the limit of “massive” systems, which, like the nanosphere, consist of hundreds of millions of atoms [11]. By demonstrating a measurement of photon recoil heating, Novotny’s group has unambiguously observed the first signatures of quantum phenomena on optically levitated nanoparticles.

This research is published in Physical Review Letters.

References

B. P. Abbott et al., “Observation of Gravitational Waves from a Binary Black Hole Merger,” Phys. Rev. Lett. 116, 061102 (2016).
V. Jain, J. Giesler, C. Moritz, C. Dellago, R. Quidant, and L. Novotny, “Direct Measurement of Photon Recoil from a Levitated Nanoparticle,” Phys. Rev. Lett. 116, 243601 (2016).
A. Ashkin, “Optical Trapping and Manipulation of Neutral Particles Using Lasers,” Opt. Photon. News 10, 41 (1999).
G. Ranjit, M. Cunningham, K. Casey, and A. A. Geraci, “Zeptonewton Force Sensing with Nanospheres in an Optical Lattice,” Phys. Rev. A 93, 053801 (2016).
T. Li, S. Kheifets, and M. G. Raizen, “Millikelvin Cooling of an Optically Trapped Microsphere in Vacuum,” Nature Phys. 7, 527 (2011).
N. Kiesel, F. Blaser, U. Delić, D. Grass, R. Kaltenbaek, and M. Aspelmeyer, “Cavity Cooling of an Optically Levitated Submicron Particle,” Proc. Natl. Acad. Sci. 110, 14180 (2013).
P. Asenbaum, S. Kuhn, S. Nimmrichter, U. Sezer, and Markus Arndt, “Cavity Cooling of Free Silicon Nanoparticles in High Vacuum,” Nature Commun. 4, 2743 (2013).
J. Gieseler, B. Deutsch, R. Quidant, and L. Novotny, “Subkelvin Parametric Feedback Cooling of a Laser-Trapped Nanoparticle,” Phys. Rev. Lett. 109, 103603 (2012).
O. Romero-Isart, M. L. Juan, R. Quidant, and J. I. Cirac, “Toward Quantum Superposition of Living Organisms,” New J. Phys. 12, 033015 (2010).
D. E. Chang, C. A. Regal, S. B. Papp, D. J. Wilson, J. Ye, O. Painter, H. J. Kimble, and P. Zoller, “Cavity Opto-Mechanics Using an Optically Levitated Nanosphere,” Proc. Natl. Acad. Sci. 107, 1005 (2009).
R. Kaltenbaek, G. Hechenblaikner, N. Kiesel, O. Romero-Isart, K. C. Schwab, U. Johann, and M. Aspelmeyer, “Macroscopic Quantum Resonators (MAQRO): Testing Quantum and Gravitational Physics with Massive Mechanical Resonators,” Exp. Astronomy 34, 123 (2012).

About the Author

Amir Safavi-Naeini is an Assistant Professor of Applied Physics at Stanford University. He received his Ph.D. at the California Institute of Technology, where he worked with Oskar Painter, and then conducted a year of postdoctoral research with Andreas Wallraff at the ETH, Zurich. As a graduate student, he and his colleagues succeeded in observing the first nonclassical phenomena with optomechanical devices. At Stanford, his group tries to find new ways of harnessing quantum complexity in chip-scale microwave, optical, and mechanical circuits.