Classical Simulation of Quantum Systems?
The field of quantum computing originated with a question posed by Richard Feynman. He asked whether or not it was feasible to simulate the behavior of quantum systems using a classical computer, suggesting that a quantum computer would be required instead [1]. Saleh Rahimi-Keshari from the University of Queensland, Australia, and colleagues [2] have now demonstrated that a quantum process that was believed to require an exponentially large number of steps to simulate on a classical computer could in fact be simulated in an efficient way if the system in which the process occurs has sufficiently large loss and noise.
The quantum process considered by Rahimi-Keshari et al. is known as boson sampling, in which the probability distribution of photons (bosons) that undergo a linear optical process [3] is measured or sampled. In experiments of this kind [4, 5], single photons are sent into a large network of beams splitters (half-silvered mirrors) and combined before exiting through possible output channels. The calculation of the probability distribution for finding the photons in each of the output channels is equivalent to calculating the permanent of a matrix. The permanent is the same as the more familiar determinant but with all of the minus signs replaced with plus signs. On any classical computer, the number of computational steps required to calculate the permanent of a matrix is believed to increase exponentially with increasing values of [3], which would make the problem impossible to solve for large values of .
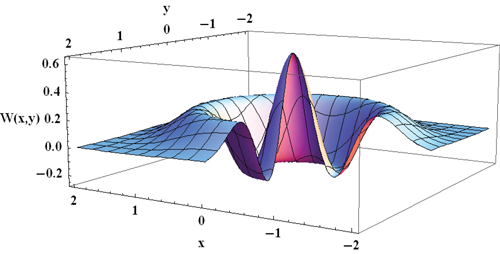
Rahimi-Keshari and colleagues argue that simulating boson-sampling experiments is not as difficult as calculating the permanent of a matrix if the loss and noise in the experiments are sufficiently large. Their theoretical proof is based on the use of quasiprobability distributions [6, 7], such as the Wigner distribution. As a simple example, the Wigner distribution for a state containing two photons in a single channel is shown in Fig. 1. Quasiprobability distributions have many of the same properties as classical probability distributions, but the Wigner distribution can have negative values, which demonstrates the quantum-mechanical nature of the system. The researchers showed that, for sufficiently large loss and noise, the Wigner distribution describing the photons was positive and, therefore, that the results of the experiment could be simulated classically without requiring an exponentially large number of computational steps.
This proof does not overturn Feynman’s suggestion about the need for quantum simulation in general but clarifies when it applies. A boson-sampling system is a simple but representative case of a quantum system that, when large enough, is seemingly unsolvable with a classical computer. Rahimi-Keshari and co-workers’ study is significant in that it provides upper bounds on the experimental conditions in order for that to be the case.
These results are closely related to the fact that the experimental errors in a quantum computer must be sufficiently small in order to perform quantum error correction. The information in a quantum computer is represented by qubits, which can take on various physical forms, including single photons, trapped ions, electronic spins, and superconducting Josephson junctions. Error correction involves identifying and correcting experimental errors that affect the fragile states of the qubits without disturbing their values. Protocols for quantum error correction have a maximum allowed error rate, which is typically calculated using a “top-down” approach that uses quantum information techniques that are independent of the physical nature of the qubits. The methods used by Rahimi-Keshari et al. might allow a “bottom-up” approach in which the physical properties of the qubits themselves can be used to bound the maximum error rate for a quantum computation that cannot be simulated classically.
Experimental tests of nonlocality typically involve mathematical inequalities that bound the predictions of classical field theories [8] or local hidden variable theories. [9]. Quantum mechanics predicts the violation of these inequalities, but this can only be observed if the experimental errors are sufficiently small, which is similar to the situation for boson sampling or quantum computing. To date, these inequalities have applied only to specific experimental setups, such as tests of Bell’s inequality [9]. It may be possible to apply the techniques used in the study by Rahimi-Keshari and co-workers to derive other types of inequalities or more general bounds on the predictions of any classical theory.
Quantum computers are expected to be able to solve certain problems that are not feasible on a classical computer, such as factoring large integers. To the best of my knowledge, there is no rigorous proof that quantum computers can provide an exponential speed-up compared to classical computers [10]. For example, the argument that boson sampling cannot be simulated classically (even in the limit of no experimental errors) is based on the assumption that various computational complexity classes are not equivalent [3]; certain kinds of calculations require many more steps than others using the best-known algorithms, and this is believed to be true for any algorithm. Perhaps Rahimi-Keshari and colleagues’ approach could be used to avoid the need for this assumption. That would be an important step towards answering Feynman’s original question [1] in a more rigorous way.
This research is published in Physical Review X.
References
- R. P. Feynman, “Simulating Physics with Computers,” Int. J. Theor. Phys 21, 467 (1982).
- S. Rahimi-Keshari, T. C. Ralph, and C. M. Caves, “Sufficient Conditions for Efficient Classical Simulation of Quantum Optics,” Phys. Rev. X 6, 021039 (2016).
- S. Aaronson and A. Arkhipov, “The Computational Complexity of Linear Optics,” in Proceedings of the ACM Symposium on the Theory of Computing, STOC (Association for Computing Machinery, New York, 2011), p. 33[Amazon][WorldCat].
- J. B. Spring et al., “Boson Sampling on a Photonic Chip,” Science 339, 798 (2013).
- M. Tillmann, B. Dakic, R. Heilmann, S. Nolte, A. Szameit, and P. Walther, “Experimental Boson Sampling,” Nature Photon. 7, 540 (2013).
- R. A. Brewster and J. D. Franson, “Generalized Delta Functions and Their Use in Quasi-Probability Distributions,” arXiv:1605.04321.
- W. P. Schleich, Quantum Optics in Phase Space (Wiley-VCH, Berlin, 2001)[Amazon][WorldCat].
- J. D. Franson, “Violations of a Simple Inequality for Classical Fields,” Phys. Rev. Lett. 67, 290 (1991).
- J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics (Long Island City) 1, 195 (1964).
- M. J. Bremner, R. Jozsa, and D. J. Shepherd, “Classical Simulation of Commuting Quantum Computations Implies Collapse of the Polynomial Hierarchy,” Proc. R. Soc. London A 467, 459 (2010).