Fermionic Vortices Find their Dual
Dirac fermions in 2+1 dimensions (two spatial dimensions plus time) have been found in graphene and on the surfaces of topological insulators (TIs). A trio of papers now shows that these particles can also be found in a dual description of quantum electrodynamics (QED) [1–3]. This deceptively simple statement joins together several disparate lines of progress in theoretical physics: interacting topological insulators, anomalies in quantum field theory, spin liquids, and compressible quantum Hall states.
Humans are not very good at understanding interacting many-body systems. We understand the behavior of free particles and can sometimes use perturbation theory to incorporate weak interactions between them. But what happens when we couple the particles strongly? To reveal the interesting collective phenomena that can result, we’ve had to rely largely on experiments. Examples include superconductivity, superfluidity, the integer and fractional quantum Hall effects, the fractionalization of charge and spin, and the wetness of water.
Duality is the circumstance in which cranking up interactions results in another system we understand, usually one that can be described in terms of another set of weakly coupled particles. When such a dual representation is found, it gives a solution to the strong coupling problem. A further reason that theoretical physicists get excited about dualities is that they undermine the very notion of an “elementary particle.” In terms of the original variables, the dual, weakly coupled particles are generally solitons—large, heavy, classical objects made up of many quanta. The remarkable thing is that solitons can become “elementary,” in the sense that the model that describes the system can be reformulated with the solitons as the basic constituents. An example of a duality, which we will use below, arises in Maxwell’s theory of electromagnetism, where the strength of the interactions is determined by the electric charge . The duality exchanges electric and magnetic point charges, and the interaction strength in the dual description is , which is small when is large. This idea has been generalized to many other field theories, thanks, in particular, to tools of supersymmetry [4].
Another classic example of duality involves vortices. A vortex is a localized object in the plane around which a phase field winds. (A phase field takes values on the circle.) Dualities relating particles and vortices have a rich history in particle physics and condensed-matter physics. The simplest version relates the particles in the normal state of a superfluid to the vortices in a dual superconductor [5]. This charge-vortex duality has been a workhorse in the study of two-dimensional condensed-matter systems, such as fractional quantum Hall states, superconducting thin films, and beyond-Landau critical phenomena [6].
Vortices can be fermions. A dual description of a system with fermionic vortices thus requires a new ingredient, since it must include such a fermionic particle. The new work [1–3] builds on earlier theoretical work [7] to make an appealing proposal for the required duality: the fermionic vortex of QED in 2+1 dimensions is a free Dirac fermion. The argument for this proposal builds on our understanding of TIs.
TIs are distinguished only by their edge states. The most famous example is a (3+1)-dimensional time-reversal invariant TI, which can host boundary states whose band structure is defined by a single Dirac cone. A single time-reversal-symmetric Dirac cone is not possible without the bulk TI, so its appearance in experiments provides a signature of the bulk phase. But the Dirac cone is not the only possible signature. Deformations of the boundary conditions can dramatically change the spectrum of the edge states, yet preserve some essential “TI-ness.” This essential property is called an anomaly in high-energy theory.
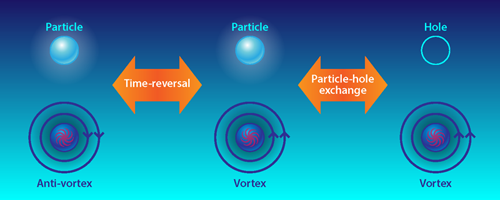
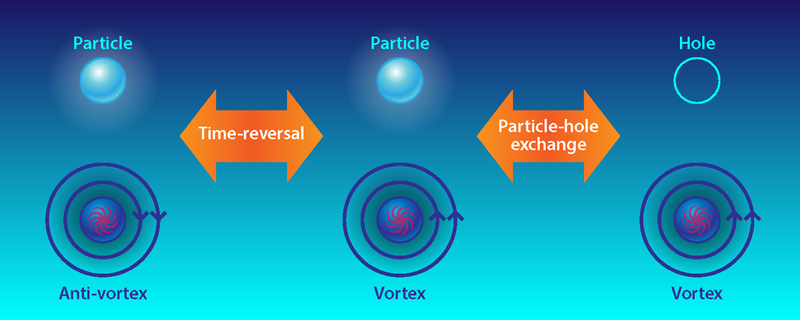
Max Metlitski of the University of California, Santa Barbara, and Ashvin Vishwanath of the University of California, Berkeley [1], and independently, Chong Wang and Todadri Senthil at the Massachusetts Institute of Technology, Cambridge [2], use this ambiguity in the edge theory and the electric-magnetic duality of an auxiliary theory of bulk electromagnetism coupled to the TI to argue for the duality. When I said that (3+1)-dimensional QED had a duality that interchanged the electric and magnetic charges, one could have complained that the electron is a fermion, while a magnetic monopole may not be. However, the authors observe that in a TI, a charge-two monopole is also a fermion. By analyzing the spectrum of electric and magnetic charges, they conclude that the duality exchanges the electron and the charge-two monopole and, moreover, exchanges a TI with time-reversal symmetry with a “chiral TI,” which instead has particle-hole symmetry. But this is just what is required of a symmetry that exchanges a fermionic particle with a fermionic vortex: time-reversal symmetry maps the electron to itself but maps the vortex to another vortex whose phase winds the other way (see Fig. 1). The exchange of particles and holes, in turn, preserves the vortex. The bulk duality implies a duality between edge theories.
The freedom to deform the edge of the TI implies a weak form of equivalence: although the edge theories are topologically the same (in terms of symmetry assignments and anomalies), they need not have identical low-energy physics. One side of the duality is a free, massless Dirac particle, but the long-distance physics of (2+1)-dimensional QED is a long-standing problem, which is important in the study of spin liquids. Many gauge theories in two dimensions develop a gap in their energy spectrum because of the proliferation of monopoles. In the realization proposed by Metlitski and Vishwanath [1] and by Wang and Senthil [2], this cannot happen because the monopoles carry electric charge, and indeed the stronger notion of duality as an equivalence of low-energy physics may hold. Evidence for the stronger relation comes from David Mross and colleagues at the California Institute of Technology, Pasadena [3], who have derived a lattice version of the duality using a clever but explicit change of variables. Their construction is particularly interesting because it uses a lattice of one-dimensional models which themselves can only occur at the edge of a TI.
These developments solve outstanding theoretical puzzles about interacting TIs and their symmetric, gapped, topologically ordered surface states [1, 2], and they have inspired furious activity in the field. The “auxiliary” bulk gauge theory formulated in Refs. [1, 2] actually predicts a novel (3+1)-dimensional spin liquid with time-reversal symmetry [8], which is a candidate description of certain pyrochlore magnets. Perhaps most interesting is the connection to the manifestly particle-hole symmetric theory of a half-filled Landau level [7], the best-understood non-Fermi liquid state. Briefly, the successful theory of this state makes a distinction between half-filled and half-empty electronic bands. The associated particle-hole symmetry is emergent, and an exact local realization can only occur at the edge of a TI. The main outcome is a new understanding of the Dirac-like nature of the composite fermion excitation of this system, which provides a new point of view on the phenomenology [7, 9]. This circle of ideas has also led to new insights [10] on two-dimensional superfluid-insulator transitions with nearby metallic phases, where the fermions come alive. More recently, consequences of the duality have been checked mathematically and numerically and the fermionic vortex duality has been fit into the wider web of field-theory dualities [11].
This research is published in Physical Review Letters, Physical Review B, and Physical Review X.
Correction (15 July 2016): Sentence 1 of paragraph 5 was changed from “Vortices can be fermions (as they frequently are, for instance, in type-II superconductors)” to “Vortices can be fermions.”
References
- M. A. Metlitski and A. Vishwanath, “Particle-Vortex Duality of Two-Dimensional Dirac Fermion from Electric-Magnetic Duality of Three-Dimensional Topological Insulators,” Phys. Rev. B 93, 245151 (2016).
- Chong Wang and T. Senthil, “Dual Dirac Liquid on the Surface of the Electron Topological Insulator,” Phys. Rev. X 5, 041031 (2015).
- D. F. Mross, J. Alicea, and O. I. Motrunich, “Explicit Derivation of Duality Between a Free Dirac Cone and Quantum Electrodynamics in (2+1) Dimensions,” Phys. Rev. Lett. 117, 016802 (2016).
- For more examples and references, I recommend J. Polchinski, “Dualities of Fields and Strings,” arXiv:1412.5704; Evidence can be found for the duality symmetry of Abelian gauge theory on the lattice, in J. L. Cardy and E. Rabinovici, “Phase structure of Zp models in the presence of a parameter,” Nucl. Phys. B 205, 1 (1982); J. L. Cardy, “Duality and the Parameter in Abelian Lattice Models,” 205, 17 (1982); In the continuum, see E. Witten, “On S-duality in Abelian Gauge Theory,” Selecta Math. 1, 383 (1995); Erik Verlinde, “Global Aspects of Electric-Magnetic Duality,” Nucl. Phys. B 455, 211 (1995).
- T. Banks, R. Myerson, and J. Kogut, “Phase Transitions in Abelian Lattice Gauge Theories,” Nucl. Phys. B 129, 493 (1977); M. E. Peskin, “Mandelstam-'t Hooft Duality in Abelian Lattice Models,” Ann. Phys. 113, 122 (1978); P. R. Thomas and M. Stone, “Nature of the Phase Transition in a Non-Linear O(2)-3 Model,” Nucl. Phys. B 144, 513 (1978); C. Dasgupta and B. I. Halperin, “Phase Transition in a Lattice Model of Superconductivity,” Phys. Rev. Lett. 47, 1556 (1981); M. P. A. Fisher and D. H. Lee, “Correspondence between Two-Dimensional Bosons and a Bulk Superconductor in a Magnetic Field,” Phys. Rev. B 39, 2756 (1989).
- M. P. A. Fisher and D. H. Lee, “Correspondence between Two-Dimensional Bosons and a Bulk Superconductor in a Magnetic Field,” Phys. Rev. B 39, 2756 (1989); D.-H. Lee and M. P. A. Fisher, “Anyon Superconductivity and the Fractional Quantum Hall Effect,” Phys. Rev. Lett. 63, 903 (1989); M. P. A. Fisher, G. Grinstein, and S. M. Girvin, “Presence of Quantum Diffusion in Two Dimensions: Universal Resistance at the Superconductor-Insulator Transition,” 64, 587 (1990); T. Senthil, L. Balents, S. Sachdev, A. Vishwanath, and M. P. A. Fisher, “Quantum Criticality Beyond the Landau-Ginzburg-Wilson Paradigm,” Phys. Rev. B 70, 144407 (2004).
- D. T. Son, “Is the Composite Fermion a Dirac Particle?,” Phys. Rev. X 5, 031027 (2015).
- C. Wang and T. Senthil, “Time-Reversal Symmetric U ( 1 ) Quantum Spin Liquids,” Phys. Rev. X 6, 011034 (2016); “Half-Filled Landau Level, Topological Insulator Surfaces, and Three-Dimensional Quantum Spin Liquids,” Phys. Rev. B 93, 085110 (2016).
- B. I. Halperin, P. A. Lee, and N. Read, “Theory of the Half-Filled Landau Level,” Phys. Rev. B 47, 7312 (1993); C. Wang and T. Senthil, “Half-filled Landau Level, Topological Insulator Surfaces, and Three-Dimensional Quantum Spin Liquids,” 93, 085110 (2016); G. Murthy and R. Shankar, “ Landau Level: Half-Empty versus Half-Full,” 93, 085405 (2016); C. Wang and T. Senthil, “Composite fermi liquids in the lowest Landau level,” arXiv:1604.06807; See J. Alicea, “Composite fermions meet Dirac,” Journal Club for Condensed Matter Physics (Sep, 2015) http://www.condmatjournalclub.org/?p=2655..
- M. Mulligan and S. Raghu, “Composite Fermions and the Field-Tuned Superconductor-Insulator Transition,” Phys. Rev. B 93, 205116 (2016); M. Mulligan, “Particle-Vortex Symmetric Liquid,” arXiv:1605.08047.
- S. D. Geraedts, M. P. Zaletel, R. S. K. Mong, M. A. Metlitski, A. Vishwanath, and O. I. Motrunich, “The Half-Filled Landau Level: The Case for Dirac Composite Fermions,” Science 352, 197 (2016); Further strong mathematical evidence for the duality relating electromagnetism coupled to class AII and class AIII TIs: M. A. Metlitski, “S-Duality of u(1) Gauge Theory with on Non-Orientable Manifolds: Applications to Topological Insulators and Superconductors,” arXiv:1510.05663; Web of dualities: A. Karch and D. Tong, “Particle-Vortex Duality from 3d Bosonization,” arXiv:1606.01893; J. Murugan and H. Nastase, “Particle-Vortex Duality in Topological Insulators and Superconductors,” arXiv:1606.01912 ; N. Seiberg, T. Senthil, C. Wang, and E. Witten, “A Duality Web in 2+1 Dimensions and Condensed Matter Physics,” arXiv:1606.01989.