Liquid Light with a Whirl
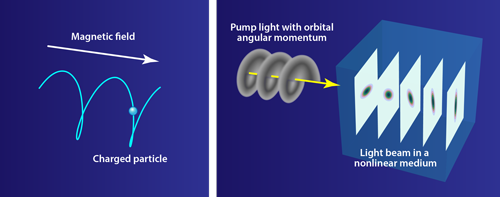
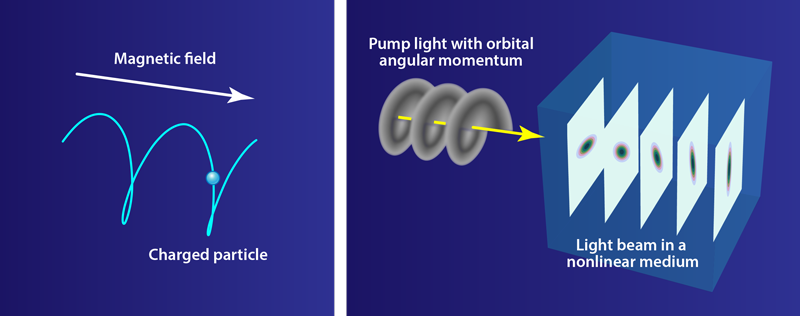
Magnetism and rotation have a lot in common. The effect of a magnetic field on a moving charge, the Lorentz force, is formally equivalent to the fictitious force felt by a moving mass in a rotating reference frame, the Coriolis force. For this reason, atomic quantum gases under rotation can be used as quantum simulators of exotic magnetic phenomena for electrons, such as the fractional quantum Hall effect. But there is no direct equivalent of magnetism for photons, which are massless and chargeless. Now, Niclas Westerberg and co-workers at Heriot-Watt University, UK, have shown how to make synthetic magnetic fields for light [1]. They developed a theory that predicts how a light beam in a nonlinear optical medium pumped by “twisted light” will rotate as it propagates, just as an electron will whirl around in a magnetic field. More than that, the light will expand as it goes, demonstrating fluid-like behavior. We can expect synthetic magnetism for light to bring big insights into magnetism in other systems, as well as some beautiful images.
The idea that light can behave like a fluid and, even more interestingly, a superfluid (a fluid with zero viscosity), goes back at least to the 1990s [2]. The analogy comes about because Maxwell’s equations for nearly collimated light in a nonlinear medium look like the Schrödinger equation for a superfluid of matter, modified to include particle interactions. Fluids of light, or photon fluids, propagating in bulk nonlinear media show a range of fluid and superfluid behavior, such as free expansion and shock waves [3]. In microcavities, fluids of light can be strongly coupled to matter, such as semiconductor electron-hole pairs, to make hybrid entities known as polariton condensates [4]. These condensates can exhibit quantized vortices, which are characteristic of superfluidity [5]. Despite these impressive advances, it has proven difficult to induce the strong bulk rotation required for phenomena such as the quantum Hall effect to show up in photon fluids, hence the need for synthetic magnetism.
The concept of synthetic magnetism is borrowed from ultracold atoms. With atoms, it is experimentally unfeasible to reach a regime of rapid rotation corresponding to a large magnetic field, not least because the traps that confine the atoms are unable to provide the centripetal force to stop them from flying out. Instead, it is possible to take advantage of the fact that atoms have multiple internal states. These can be used to generate geometric phases, as opposed to dynamic phases (which can be imposed by any forces, whatever the structure of the internal states may be). A geometric phase, otherwise known as a Berry phase [6], arises when a system’s internal states (for example, its spin) smoothly follow the variations of an external field, so that its phase depends on which path it takes between two external states (for example, two positions of the system), even if the paths have the same energy. In atomic systems, the variations of the external field in position are achieved with phase or amplitude structures of the electromagnetic field of laser light [7]. These variations can be engineered to produce the rotational equivalent of the vector potential for a magnetic field on a charged particle, inducing strong bulk rotation that shows up as many vortices in a superfluid Bose-Einstein condensate [8].
To produce a geometric phase in a fluid of light, Westerberg and colleagues considered light with two coupled internal states—a spinor photon fluid. They studied two types of nonlinear media, with second- and third-order optical nonlinearities, respectively. The second-order nonlinearity comes in the form of mixing of three fields in a birefringent crystal, in which one field, the pump light field, splits into two further fields with orthogonal polarizations, these being the two required internal states of the spinor fluid. Slow spatial variations of the strong pump field generate a synthetic vector potential that is equivalent to a magnetic field for electric charges or rotation for atoms.
The third-order optical nonlinearity occurs in a medium with a refractive index that depends on the intensity of light. The spinor photon fluid in this case consists of weak fluctuations around a strong light field that carries orbital angular momentum (colloquially known as twisted light). The two internal states of the fluid are distinguished by their differing orbital angular momentum. The resulting vector potential produces synthetic magnetism, much as with the second-order nonlinearity. Coincidentally, for the medium with a second-order nonlinearity, Westerberg and co-workers also propose using twisted light.
The authors present numerical simulations for both types of nonlinearity. For the second-order nonlinear medium, they show that an elliptical light beam in a synthetic magnetic field rotates about its propagation axis and expands as it propagates (Fig 1). The expansion shows that the light is behaving as a fluid in rotation. For the third-order nonlinear medium there is a trapped vortex that causes the beam to rotate, which is akin to cyclotron motion of a charge in a magnetic field. Short of spinning the medium extremely rapidly [9], it is not obvious how one could otherwise make a beam continuously rotate as it propagates.
Westerberg and colleagues’ work makes important connections between several disparate topics: nonlinear optics, atomic physics, geometric phases, and light with orbital angular momentum. Spinor photon fluids in themselves are a new development. The complete state of a photon fluid—its amplitude, phase, and polarization—can be mapped out; this is not possible for atoms or electrons. Some of the authors of the present study have recently experimentally driven photon fluids past obstacles in ways that are hard to achieve for atoms, and obtained evidence for superfluidity through the phase of the photon fluid [10]—evidence that cannot be obtained for electronic magnetism. Furthermore, they have also made photon fluids that have nonlocal interactions, via thermal effects. Generalizing synthetic magnetism to nonlocal fluids of light will enlighten us about magnetism and rotation in solid-state and atomic superfluids. Experimental implementation will surely follow hot on the heels of this proposal.
This research is published in Physical Review A.
References
- N. Westerberg, C. Maitland, D. Faccio, K. Wilson, P. Öhberg, and E. M. Wright, “Synthetic Magnetism for Photon Fluids,” Phys. Rev. A 94, 023805 (2016).
- L. A. Lugiato and R. Lefever, “Spatial Dissipative Structures in Passive Optical Systems,” Phys. Rev. Lett. 58, 2209 (1987); R. Y. Chiao and J. Boyce, “Bogoliubov Dispersion Relation and the Possibility of Superfluidity for Weakly Interacting Photons in a Two-Dimensional Photon Fluid,” Phys. Rev. A 60, 4114 (1999).
- W. Wan, S. Jia, and J. W. Fleischer, “Dispersive Superfluid-Like Shock Waves in Nonlinear Optics,” Nature Phys. 3, 46 (2006).
- I. Carusotto and C. Ciuti, “Quantum Fluids of Light,” Rev. Mod. Phys. 85, 299 (2013).
- A. Amo, J. Lefrère, S. Pigeon, C. Adrados, C. Ciuti, I. Carusotto, R. Houdré, E. Giacobino, and A. Bramati, “Superfluidity of Polaritons in Semiconductor Microcavities,” Nature Phys. 5, 805 (2009).
- M. V. Berry, “Quantal Phase Factors Accompanying Adiabatic Changes,” Proc. R. Soc. London A 392, 45 (1984).
- J. Dalibard, F. Gerbier, G. Juzeliūnas, and P. Öhberg, “Colloquium : Artificial Gauge Potentials for Neutral Atoms,” Rev. Mod. Phys. 83, 1523 (2011).
- Y.-J. Lin, R. L. Compton, K. Jiménez-García, J. V. Porto, and I. B. Spielman, “Synthetic Magnetic Fields for Ultracold Neutral Atoms,” Nature 462, 628 (2009).
- S. Franke-Arnold, G. Gibson, R. W. Boyd, and M. J. Padgett, “Rotary Photon Drag Enhanced by a Slow-Light Medium,” Science 333, 65 (2011).
- D. Vocke, K. Wilson, F. Marino, I. Carusotto, E. M. Wright, T. Roger, B. P. Anderson, P. Öhberg, and D. Faccio, “Role of Geometry in the Superfluid Flow of Nonlocal Photon Fluids,” Phys. Rev. A 94, 013849 (2016).