Curling Up Extra Dimensions in String Theory
The ultimate goal of string theory is not only to unify quantum mechanics with general relativity, but also to explain the spectrum of particles and forces observed in nature. Matrix theory, the latest formulation of string theory, has eleven spacetime dimensions. Its proponents have struggled with the most vexing problem of all such theories: explaining exactly how the extra dimensions are “compactified” to make them unobservable in our four-dimensional world. Compactification also specifies most of the interesting properties of such a theory. In the 6 April PRL, a team of string theorists makes a leap toward solving the compactification problem for matrix theory.
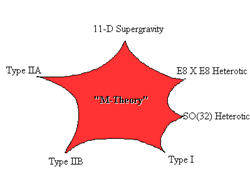
String theory posits that the world is made of incredibly small strings vibrating in a ten-dimensional spacetime. Three years ago it was discovered that the five distinct types of string theory were actually different limits of “M theory,” an eleven-dimensional theory that includes supergravity. There is no consensus on the meaning of the “M,” but many string theorists take it to stand for “membrane,” since the theory contains vibrating surfaces of several different dimensions. M theory lacks precise equations of motion, but in 1996, Tom Banks, of Rutgers University in Piscataway, NJ, and his colleagues proposed that M theory might be described by ”matrix theory,” whose basic variables are matrices.
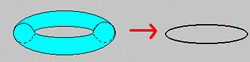
But compactifying this eleven-dimensional theory down to four dimensions has been challenging. Compactifying means “curling up” extra dimensions of the theory to a very small size. To curl up two dimensions, for example, take a doughnut (a two-dimensional surface), and begin by squeezing it down to a circular wire with an unobservably small cross section. Then squeeze the wire loop down to a point. Without a probe sensitive enough to detect the “shrunken” dimensions, the wire appears one dimensional, and the point appears to have zero dimensions. In M theory that scale, which is of order 10-33 cm, is well beyond the reach of present-day probes, so after compactifying seven tdimensions it seems as though we live in only four dimensions.
In this week’s PRL, Shamit Kachru, of the University of California at Berkeley, Albion Lawrence, of Harvard University, and Eva Silverstein, of the Stanford Linear Accelerator Center in Stanford, CA, tackle the problem of compactifying six dimensions–going from eleven dimensions down to five. (“Qualitatively new” problems arise, according to Kachru, if they try to extend their approach down to four dimensions.) Compactifying six dimensions of matrix theory using a six-dimensional torus (doughnut), a conventional choice, is difficult because the surface has many holes. It also leads to a theory with more symmetries than are observed in nature because tori are too symmetric–they are invariant under many different rotations and reflections. A correct theory must be compactified using a complicated six-dimensional space called a Calabi-Yau manifold, which has fewer symmetries than a six-torus.
There have been many attempts at the first exercise–compactifying matrix theory using a six-torus–but none have succeeded. No one considered trying the presumed harder problem of compactifying with Calabi-Yau manifolds, even though it was known that would utlimately be necessary for a valid theory. But to the surprise of Kachru and his colleagues, it is actually easier to compactify matrix theory with Calabi-Yau manifolds than with six-tori. Calabi-Yau manifolds have fewer holes, which avoids some complications in matrix theory and outweighs the difficulties caused by the complexity of their manifolds. “Matrix theory might teach you why strings like to be compactified on one manifold as opposed to another,” says Kachru.
String theorists are still far from knowing whether matrix theory represents the world at very small scales. But according to Edward Witten, of the Institute for Advanced Study in Princeton, NJ, “it is surprising how one can build a theory that includes gravity from a starting point that includes only gauge theory.”
–Robert Garisto
Robert Garisto is the Chief Editor of Physical Review Letters.