Landmarks: Powerful Pictures
Focus Landmarks feature important papers from the archives of the Physical Review.
Every popular explanation of particle physics is liberally illustrated with cartoon-like pictures of straight and wiggly lines representing electrons, photons, and quarks, interacting with one another. These so-called Feynman diagrams were introduced by Richard Feynman in the Physical Review in 1949, and they quickly became an essential tool for particle physicists. Early on, Feynman struggled to explain the meaning of the diagrams to his fellow physicists. But using them, he came up with easy answers to difficult problems in quantum mechanics and ultimately won a share of the Nobel Prize.
Through the 1940s, theoretical physicists were wrestling with infinities. They arose from the “self-energy” that electrons and other charged particles possess because their charge interacts with their own electromagnetic field. This self-energy contributes, through the equivalence of mass and energy, to the particle’s mass. But all attempts to calculate self-energy yielded infinite results, which stymied attempts to evaluate such basic processes as the scattering of an electron by a photon.
The answer to this difficulty was a trick known as “renormalization.” Crudely put, the idea was to give the electron an infinite “bare” mass that was amended by the infinite correction arising from self-energy. The measured mass–the difference between these two infinities–could then be made finite. Performing this mathematical balancing act was challenging, but in 1948, Julian Schwinger of Harvard University calculated the self-energy as the sum of an infinite series of progressively smaller terms and showed that renormalization could tame the infinities arising from each term in the series. A Japanese theorist, Sin-Itiro Tomonaga, independently came up with a similar demonstration [1].
Richard Feynman, then a young professor at Cornell University, also solved the problem, but in an idiosyncratic way: he drew pictures, with smooth lines representing electrons and wavy lines representing photons. The vertical axis was time, with space on the horizontal. One contribution to the electron’s self-energy, for example, was a photon emitted by the electron and then quickly reabsorbed by it–a vertical line with a wavy line that starts and ends on the electron line. This “virtual” photon can appear out of nowhere because its energy and lifetime are below the limit set by the uncertainty principle–meaning that the photon is strictly unobservable. Feynman drew other more complicated self-interactions with more virtual photons and electrons appearing and disappearing and then wrote down mathematical formulas for each diagram’s contribution to the self-energy. A series of such pictures was his starting point for any calculation.
At a conference in the Poconos mountains, in Pennsylvania, in March 1948, Schwinger gave a marathon presentation that exhausted but impressed his audience. A frustrated Feynman, however, failed during his talk to convince the attending physicists of the soundness of his methods. Elder statesmen such as Paul Dirac and Niels Bohr concluded that the young American simply did not understand quantum mechanics.
But Feynman was able to solve complex problems far more quickly than those using the Schwinger formulation. Clarification came from Freeman Dyson, of the Institute for Advanced Study in Princeton, New Jersey, who showed in a classic paper that the Schwinger, Tomonaga, and Feynman methods were equivalent [2].
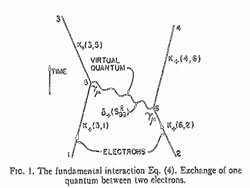
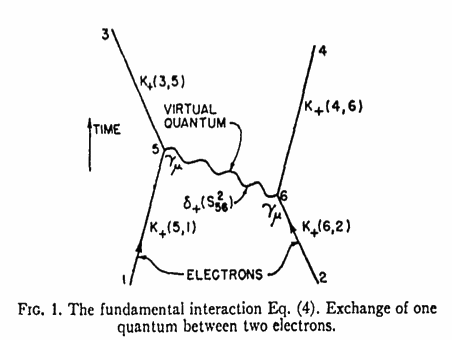
The first published example of what is now called a Feynman diagram appeared in Feynman’s 1949 Physical Review article. It depicted the simplest contribution to an electron-electron interaction, with a single virtual photon (wavy line) emitted by one electron and then absorbed by the other. In Feynman’s imagination–and in the equations–this diagram also represented interactions in which the photon is emitted by one electron and travels back in time to be absorbed by the other, which is allowed within the Heisenberg time uncertainty.
More complex versions of the electron-electron interaction, involving additional virtual photons and electrons, correspond to contributions that were extremely hard to write down mathematically using the Schwinger-Tomonaga approach. So it isn’t surprising that Feynman’s diagrams were quickly adopted by the physics community, says Sylvan Schweber of Brandeis University in Waltham, Massachusetts. Feynman, Schwinger and Tomonaga shared the 1965 Nobel Prize in physics.
–David Lindley
David Lindley is a freelance science writer in Alexandria, Virginia.
References
- S. Tomonaga and J. R. Oppenheimer, “On Infinite Field Reactions in Quantum Field Theory,” Phys. Rev. 74, 224 (1948); J. Schwinger, “Quantum Electrodynamics. I. A Covariant Formulation,” Phys. Rev. 74, 1439 (1948)
- F. J. Dyson, “The Radiation Theories of Tomonaga, Schwinger, and Feynman,” Phys. Rev. 75, 486 (1949)