How colloidal dispersions relax under stress

Norman J. Wagner

Viewpoint

How colloidal dispersions relax under stress

Department of Chemical Engineering, University of Delaware, Newark, DE 19716, USA

September 22, 2008• Physics 1, 22

A shear force can melt a colloidal glass, causing it to flow in a highly nonlinear fashion. Physicists have now found a way to put the description of this type of flow on a more formal theoretical footing.

Figure caption — **Figure 1:** The cartoon at left shows how the motion of particles can become arrested in a colloidal dispersion. The caging mechanism occurs in concentrated dispersions: a reference particle (red) is hindered from moving by excluded volume interactions with its neighbors (blue), that are in turn are hindered by their neighbors (grey). Caging effects can make the response of the colloidal dispersion to a time varying shear force ( $\overset{\cdot}{γ}$ ) highly nonlinear. The image on the right shows a simulation of how the microstructure is distorted in the plane of shear for a concentrated hard sphere dispersion under shear flow at a relatively moderate shear rate (see [11]) [Courtesy of J. F. Brady, CalTech]

Of the many physical systems that we can study, colloids and colloid dispersions may well be one of the most prevalent in our daily lives. Inks, paints, clays, emulsions, and milk, as well as surfactant aggregates (micelles) and nanoparticle suspensions are all colloid dispersions. The study of how these dispersions and other complex liquids flow—a field called rheology—is essentially a problem of nonequilibrium statistical mechanics that must account for many-body interactions. The response of colloid dispersions to a shear force is often nonlinear and can result in interesting physical phenomena. The application of a shearing force, for example, can increase the viscosity of a dispersion, an effect that can be harnessed to make personal protective devices [1].

Predicting how a colloid dispersion responds to an external stress and connecting this relationship to the microscopic interactions between the dispersed particles is a key goal of theoretical rheology. Writing in Physical Review Letters, Joseph Brader and Matthias Fuchs of the Universität Konstanz in Germany and Michael Cates of The University of Edinburgh report the development of a rheological constitutive equation for dense colloidal suspensions and glasses [2] (here, constitutive refers to the stress-response relationship). The work links a highly successful microscopic theory, which describes how colloidal particles become arrested at the glass transition of a colloid, to a formal description of suspension rheology. Although this is not the first effort in this direction [3], the paper by Brader et al. is an important contribution because it applies to both colloidal dispersion and glasses, can describe the response for nonlinear, arbitrary deformation fields, and satisfies the criterion that the stresses should be invariant for different reference frames.

The theory of the flow of colloidal dispersion under shear has a rich history that spans over a century. The field really begins with the seminal work of Einstein in 1906 [4,5], in which he studied how single-particle motion contributes to the viscosity of a suspension. Around the same time, Smoluchowski developed a statistical description of Brownian motion of colloidal particles [6]. In the early 1970s, Batchelor formulated the stress tensor—a matrix whose components describe the forces acting on the material in all three spatial coordinates—for both hydrodynamic (that is, mediated by the fluid between the particles) and conserved interactions [7–9]. The past thirty years of theoretical development have largely focused on handling the fact that a concentrated colloid dispersion is a many-body problem, though the challenge of many-body hydrodynamic interactions is, in practice, largely resolved [10–12]. With advanced simulation methods, it is possible to obtain accurate solutions for sufficiently large ensembles of particles [13,14], even if analytical calculations are intractable for all but regular arrays.

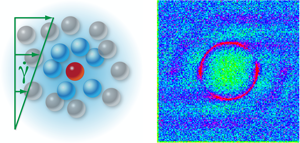
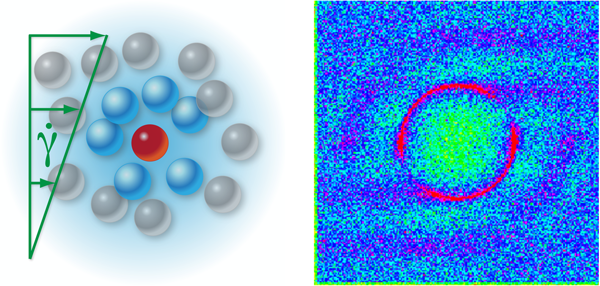
One way that many-body interactions affect particle dynamics is through excluded volume effects that result from the finite size of the dispersed particles (see Fig 1, left panel). In a sufficiently dense suspension of hard spheres, these effects can lead to the formation of a colloidal glass, a kinetic transition characterized by “dynamical arrest” of the particle motion [15]. However, when theories that are based on only pair-wise interactions between particles (rather than a many-body picture) are extended to concentrated dispersions, they do not capture this divergence in the viscosity at the ideal glass transition, but at much higher concentrations [16,17].

A promising approach for describing colloidal dynamics just above and below the colloidal glass transition has proven to be mode-coupling theory (MCT). This theory is an ansatz proposed to handle highly correlated systems and can therefore account for the particle caging shown in the left panel of Fig. 1. The relaxation modes of the test particle (the red particle) are formally coupled to those of the neighbors (blue) comprising the cage, which themselves are caged by their neighbors (grey), ad infinitum. Indeed, MCT has been shown to accurately model the diffusion of particles, at equilibrium, and the viscoelasticity for charged sphere dispersions where hydrodynamic interactions are not dominant [3,18–20] The theory also provides a qualitative framework for understanding the linkage between viscoelasticity and particle “caging” in hard-sphere dispersions [21,22].

In their new work, Brader, Cates, and Fuchs put their earlier ansatz extending MCT for colloidal suspensions to nonlinear shear deformations on a more formal footing. A significant advantage of their approach is that they fold the successful MCT description of particle dynamics into a generalized formulation of the stress tensor (in particular, they use the Green-Kubo formalism [3]). Their identification of the full tensorial structure of the theory means it is not restricted to simple shear deformation. To illustrate their approach, Brader et al. consider a hard-sphere colloidal glass and calculate the dynamic yield stress, i.e., the force required to melt the glass and cause the dispersion to flow, under shear as well as uniaxial and planar extension flows.

The theory predicts what happens to the microstructure of a colloidal suspension under an applied deformation (an example of this sort of calculation is shown in the right panel of Fig. 1). The results could be directly compared with neutron scattering measurements of the density distribution in the colloidal suspension under shear flow [23], as well as against measurements of the viscoelastic properties [24]. The calculated stress tensor agrees with previous exact derivations based on micromechanics [25] in the dilute limit (i.e., when the many-body direct correlation function reduces back to the pair potential). Differences should arise for strongly correlated systems and they can now be rigorously tested against simulations and experimental measurements. It also remains to formally determine if the stress tensor and dynamical equation that Brader et al. have calculated for the nonequilibrium microstructure are thermodynamically consistent [26].

A further challenge for the theory will be to reproduce experimental measurements of the divergence in the viscosity for hard-sphere dispersions [27]. These dispersions have a large, but finite viscosity for volume fractions above the ideal glass transition, suggesting that particle motion is activated in a way that is not captured by MCT [28]. Finally, it will at some point be necessary to include in the theory the effects of hydrodynamic interactions, which are more significant in strongly shearing or deforming dispersions.

The phase behavior and dynamics of colloidal dispersions with attractive interactions are a current topic of great scientific interest but of even greater importance in technological practice [29]. The recent successes of MCT in describing the attractive driven glass transition in colloidal dispersions [30–33] or the formation of a colloidal gel [34] suggest that the new formalism presented here might lead to accurate rheological constitutive equations for these systems, too. Further, with the formalism developed by Brader et al. it may be possible to describe time-dependent viscosities that occur in fluids exposed to changing shear (i.e., thixotropy) [35,36] as well as ageing effects [37]. Thus, this theoretical advance opens numerous opportunities for further explorations of the rich behavior of concentrated colloidal dispersions.

References

M. Decker, C. Halbach, C. Nam, N. Wagner, and E. Wetzel, Composites Science and Technology 67, 565 (2007)
J. M. Brader, M. E. Cates, and M. Fuchs, Phys. Rev. Lett. 101, 138301 (2008)
G. Nägele and J. Bergenholtz, J. Chem. Phys. 108, 9893 (1998)
A. Einstein, Ann. Phys. 324, 289 (1906)
A. Einstein, Ann. Phys. 339, 591 (1911)
M. von Smoluchowski, Ann. Phys. 326, 756 (1906)
G. K. Batchelor, J. Fluid Mech. 41, 545 (1970)
G. K. Batchelor and J. T. Green, J. Fluid Mech. 56, 401 (1972)
G. K. Batchelor and J. T. Green, J. Fluid Mech. 56, 375 (1972)
B. Cichocki, B. U. Felderhof, K. Hinsen, E. Wajnryb, and J. Bławzdziewicz, J. Chem. Phys. 100, 3780 (1994)
D R. Foss and J. F. Brady, J. Fluid Mech. 407, 167
A. Sierou and J. F. Brady, J. Rheol. 46, 1031 (2002)
A. J. Banchio and J. F. Brady, J. Chem. Phys. 118, 10323 (2003)
A. J. C. Ladd and R. Verberg, Journal of Statistical Physics 104, 1191
W. van Megen and P. N. Pusey, Phys. Rev. A 43, 5429 (1991)
J. F. Brady, J. Chem. Phys. 99, 567 (1993)
J. F. Brady, J. Chem. Phys. 98, 3335 (1993)
A. J. Banchio, G. Nägele, and J. Bergenholtz, J. Chem. Phys. 113, 3381 (2000)
A. J. Banchio, G. Nägele, and J. Bergenholtz, J. Chem. Phys. 111, 8721 (1999)
A. J. Banchio, J. Bergenholtz, and G. Nägele, Phys. Rev. Lett. 82, 1792 (1999)
T. G. Mason and D. A. Weitz, Phys. Rev. Lett. 75, 2770 (1995)
K. Miyazaki, et al., "Nonlinear viscoelasticity of metastable complex fluids," 2005 (to be published)
B. J. Maranzano and N. J. Wagner, J. Chem. Phys. 117, 10291 (2002)
J. J. Crassous, M. Siebenbürger, M. Ballauff, M. Drechsler, D. Hajnal, O. Henrich, and M. Fuchs, J. Chem. Phys. 128, 204902 (2008)
N. J. Wagner and B. J. Ackerson, J. Chem. Phys. 97, 1473 (1992)
N. Wagner, J. Non-Newton. Fluid 96, 177
Z. Cheng, J. Zhu, P. M. Chaikin, S-E. Phan, and W. B. Russel, Phys. Rev. E 65, 041405 (2002)
E. J. Saltzman and K. S. Schweizer, Phys. Rev. E 77, 051504 (2008)
R. Buscall, J. Rheol. 37, 621
E. Zaccarelli, J. Phys. Condens. Mat. 19, 323101 (2007)
P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino, and D. A. Weitz, Nature 453, 499 (2008)
J. Bergenholtz and M. Fuchs, Phys. Rev. E 59, 5706 (1999)
J. Bergenholtz and M. Fuchs, J. Phys. Condens. Mat. 11, 10171
J. Bergenholtz, W.C.K. Poon, and M. Fuchs, Langmuir 19, 4493
P. C. F. Møller, J. Mewis, and D. Bonn, Soft Matter 2, 274 (2006)
K. Dullaert and J. Mewis, J. Rheol. 49, 1213 (2005)
F. Pignon, A. Magnin, and J.-M. Piau, J. Rheol. 42, 1349 (1998)

About the Author

Norman Wagner leads an active research team at the University of Delaware that studies the rheology and nonequilibrium statistical mechanics of complex fluids. He also heads the Center for Neutron Science, a cooperative agreement with the National Center for Neutron Research at the National Institute of Standards and Technology (NIST). His research has led to inventions such as novel rheo-light scattering and rheo-SANS (small angle neutron scattering) devices, as well as STF-Armor™ (www.ccm.udel.edu/STF/).