Just-in-time DNA replication

Suckjoon Jun; Nick Rhind

Viewpoint

Just-in-time DNA replication

Suckjoon Jun

FAS Center for Systems Biology, Harvard University, Cambridge, MA 02138, USA

Nick Rhind

Biochemistry and Molecular Pharmacology, University of Massachusetts Medical School, Worcester, MA 01605, USA

October 27, 2008• Physics 1, 32

Genome replication originates at random places along the DNA strand, yet replication of the genetic material finishes within a defined time. A model based on phase-transition kinetics in condensed-matter systems explains how this just-in-time replication can happen.

Figure caption — **Figure 1:** DNA replication and the nucleation-and-growth model. (A) When water freezes, for example, nucleation sites grow to fill the entire volume (only one spatial dimension is shown as a function of time increasing upwards). (B) In cells, the last coalescent event at time $t$ between the growing replication bubbles determines the duration of DNA replication. The distribution of $ρ (t)$ depends on the “nucleation” rate $I (x, t)$ as well as the growth rate $v$ . (C) If origin firing is randomly distributed in space and time, occasional large gaps will greatly delay the completion of replication. (D) Yang and Bechhoefer have shown rigorously how the optimal timing can be achieved so all the bubbles finish at the same time . Even with a random distribution of origin firing in space, if the probability of origin firing increases with time, large gaps are efficiently replicated. Because large gaps are rare, this increased origin firing late in the replication phase does not significantly increase the total number of origins fired.

Complete and timely replication of the genome is a prerequisite to fulfilling the “dream” of every cell to become two cells . So far, biologists have been successful in identifying the processes involved in DNA replication, but they have not been able to explain a fundamental control problem that cells face, the “random-completion” or “random-gap” problem: how do cells ensure that every last piece of the genome is replicated on time ? In a paper in Physical Review E, Scott C.-H. Yang and John Bechhoefer of Simon Fraser University use insights from condensed-matter physics to answer this question . Using a physical model originally developed to describe the kinetics of first-order phase transitions, they show that, despite the intrinsic stochasticity of the initiation of DNA replication, cells can still control the amount of time it takes to replicate the genome. The authors thus provide a rigorous solution to a long-standing problem in cell biology. The elegance of their formal approach bridging physics and biology, and the depth of their analysis, should inspire scientists from both disciplines.

The heart of the problem is that the sites at which replication initiates are randomly distributed along the chromosomes of Xenopus laevis embryos, a frog widely used in cell biology experiments. There are on the order of $10^{5}$ so-called origins where replication can start in Xenopus embryos, and it was quickly realized that, if these origins were truly randomly activated, one would expect an exponential distribution of distances between origins. Such a distribution would include infrequent large gaps between origins, suggesting a total replication time longer than the 20 minutes observed in frog embryos. In fact, early workers concluded that origin distribution must not be random, for exactly that reason . However, over the years, experimental evidence for stochastic “firing” of origins has piled up. It is to this apparent conflict between stochastic origin firing and well-defined replication times that Yang and Bechhoefer bring analytical rigor.

Similar problems have confronted condensed-matter physicists. Consider a tray of water that is put into a freezer at time $t = 0$ . A short while later, the water is all frozen. What fraction $f (t)$ of water is frozen at time $t > 0$ ? In the 1930s, several scientists independently derived a stochastic model that could predict the form of $f (t)$ , and this “Kolmogorov-Johnson-Mehl-Avrami” (KJMA) model has since been widely used by metallurgists and other materials scientists to analyze phase-transition kinetics .

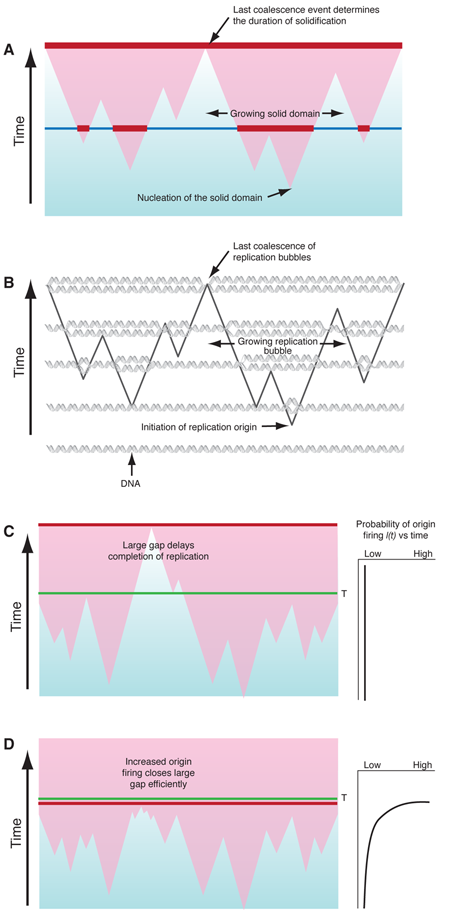
In the KJMA model, the kinetics of freezing results from three simultaneous processes: nucleation of solid domains, growth of existing domains, and coalescence, which occurs when two expanding domains merge (Fig. 1(a)). In the simplest form of KJMA, solid domains nucleate anywhere in the liquid, with equal probability $I$ for all locations. Once a solid domain has been nucleated, it grows out as a sphere, typically at constant velocity $v$ . When two growing domains impinge, growth ceases at the point of contact, while continuing elsewhere. Later workers revisited and refined KJMA’s methods to take into account various effects, such as finite system size and inhomogeneities in nucleation rates $I (x, t)$ in space and time .

About ten years ago, Bechhoefer and colleagues, who have studied nonequilibrium processes such as the growth of snowflakes, made the connection that features of DNA replication can be mapped onto the basic assumptions of the KJMA model (Fig. 1(b)): (i) DNA replication starts at a large number of origins, where replication “forks” are created, (ii) DNA synthesis propagates at replication forks bidirectionally from each activated origin, with propagation speed or fork velocity $v$ , and (iii) DNA synthesis stops when two replication forks meet. There is, however, one fundamental difference between the analysis of DNA replication and most other nucleation-and-growth systems. In crystal growth, for example, one is interested in $f (t)$ and the size distribution of “solid” and “liquid” domains for a known $I (x, t)$ , whereas in DNA replication, $I (x, t)$ itself is the unknown quantity that is important in understanding how the cell regulates the replication process in space and time. In other words, $I (x, t)$ is the replication “program” that varies from organism to organism. For example, if all the origins are initiated at the beginning of replication, then $I (x, t) = δ (t - t_{0})$ , where $t_{0}$ is the start time. Alternatively, if every origin has an equal probability of initiation at any time, then $I (x, t)$ is a constant. The question becomes, given an observed $f (t)$ , can one extract $I (x, t)$ ?

In a series of papers since 2002, Bechhoefer and colleagues have shown how one can map the DNA replication process onto the basic assumptions of the KJMA model . Importantly, by reversing the KJMA formalism, they managed to recover a spatially averaged, “mean-field” $I (t)$ from experimentally measured distributions of replicated and unreplicated domains of chromosome . To this end, they focused on the model system of Xenopus early embryo replication, in which data collection is relatively easy. It is also a perfect system to study the random-completion problem because, unlike cells of adult animals, which take many hours to replicate their genomes, these embryos finish everything in 20 minutes, making replication time a critical issue.

Biologists have proposed two solutions to the random-completion problem . The first is that replication avoids big gaps (Fig. 1(c)) altogether by using a nonrandom spacing mechanism. However, this model has received little experimental support. The second assumes there is an excess of potential origins that are randomly distributed and that origins that do not fire early in replication, but become more likely to fire as replication progresses, i.e., I(t) increases with time. The intuitive idea is that if a gap persists late in replication, it will be much more likely to have origins within it fire and thus get replicated in a timely manner. The drawback to this kind of model has been that it is not clear how robust a solution it would be.

Recently, various theoretical and experimental studies have strengthened the second view, and the emerging consensus is that there is a pool of potential origins present in Xenopus embryos and probably all other animal cells, much larger than the actual number of initiations during replication , and the probability of initiation increases steeply . However, these observations still did not completely solve the random-completion problem because the solution requires understanding the distribution (as opposed to the mean) of the replication timing for a given $I (t)$ and spatial distribution of potential origins. That is, knowing the average time it takes for replication to complete does not help; what one cares about is how often replication fails by taking longer than some threshold time $T$ .

With this in mind, Bechhoefer and co-workers interpreted the time it takes to complete replication as a “first-passage” time $t^{*}$ of a stochastic process governed by probability $I (t)$ , which concerns the distribution $ρ (t^{*})$ of a probabilistic event of interest to occur for the first time at time $t^{*}$ or, equivalently, as the largest value $t^{*}$ of the timing of collisions between two growing replication bubbles. For biological success, $t^{*}$ does not have to be less than $T$ for every cell, but the frequency of $t^{*} > T$ has to be less that some acceptable failure rate. This question belongs to the domain of extreme-value statistics (a branch of statistics that is also used to evaluate things like rare but catastrophic events), and the random-completion problem can be translated into finding conditions where $I (t, x)$ results in the observed average time to complete replication and the observed failure rate .

Yang and Bechhoefer have provided the final, clear answer to the random-completion problem: For cells to achieve an acceptable distribution of replication completion times, the initiation rate $I (t)$ should increase during replication (Fig. 1(d)), in agreement with extracted values of $I (t)$ from experimental data . They show that this model can produce arbitrarily low failure rates, but more importantly, that it can produce the observed failure rate using plausible parameters that also produce reasonable mean completion times. And finally, Yang and Bechhoefer show that their result is robust; the increasing $I (t)$ produces timely replication regardless of whether the potential origins are randomly or nonrandomly distributed. This latter point should allay biologists’ fear that in this model the replication time would double if one or two origins fail to initiate and create a gap that is too large to finish replication within 20 minutes.

Given the strong theoretic foundation provided by Yang and Bechhoefer for the increasing $I (t)$ model in frog embryos, the big question is whether this model is applicable to all animal cells. Much of this work will fall to the experimental biologists, but theoretical treatments that capture the more structured replication of adult cells will certainly be important.

References

F. Jacob, Ann. Microbiol. (Inst. Pasteur), 125B, 133 (1971)
O. Hyrien, K. Marheineke, and A. Goldar, Bioessays10.1002/bies.10208 25, 116
S. C-H. Yang and J. Bechhoefer, Phys. Rev. EPLEEE810.1103/PhysRevE.78.041917 78, 041917 (2008)
R. A. Laskey, J. Embryol. Exp. Morphol. 89, 285 (1985)
A. N. Kolmogorov, Izv. Akad. Nauk. SSSR, Ser. Fiz. [Bull. Acad. Sci. USSR, Phys. Ser.] 1, 355 (1937); W. A. Johnson and P. A. Mehl, Trans. AIMME 135, 416 (1939); M. Avrami, J. Chem. Phys.10.1063/1.1750380 7, 1103 (1939); M. Avrami, J. Chem. Phys.10.1063/1.1750631 8, 212 (1940); M. Avrami, J. Chem. Phys.10.1063/1.1750872 9, 177 (1941)
J. W. Christian, The Theory of Phase Transformations in Metals and Alloys, Part I, Volume 10080440193. Pergamon Press, New York, 3rd ed., 2002
H. Orihara and Y. Ishibashi, J. Phys. Soc. Jap.10.1143/JPSJ.61.1919 61, 1919 (1992); J. W. Cahn, Mater. Res. Soc. Symp. Proc. 398, 425 (1996); J. W. Cahn, Trans. Indian Inst. Met. 50, 573 (1997)
J. Herrick, S. Jun, J. Bechhoefer, and A. Bensimon, J. of Mol. Biol.10.1016/S0022-2836%2802%2900522-3 320, 741
S. Jun, H. Zhang, and J. Bechhoefer, Phys. Rev. EPLEEE810.1103/PhysRevE.71.011908 71, 011908 (2005); S. Jun and J. Bechhoefer, Phys. Rev. EPLEEE810.1103/PhysRevE.71.011909 71, 011909 (2005); H. Zhang and J. Bechhoefer, Phys. Rev. EPLEEE810.1103/PhysRevE.73.051903 73, 051903 (2006); S. Jun , Cell Cycle, 3, 223 (2004)
J. Bechhoefer and B. Marshall, Phys. Rev. Lett.PRLTAO10.1103/PhysRevLett.98.098105 98, 098105 (2007)
A. Goldar, H. Labit, K. Marheineke, O. Hyrien, and R. Rhind, PLoS ONE10.1371/journal.pone.0002919 3, e2919 (2008)
J. Lygeros , Proc. Natl. Acad. Sci.10.1073/pnas.0805549105 105, 12295 (2008); A. M. Woodward, The Journal of Cell Biology10.1083/jcb.200602108 173, 673 (2006)

About the Authors

Suckjoon Jun has always been obsessed with the remark by François Jacob, one of the founders of molecular biology, “The dream of every cell is to become two cells.” During his graduate studies in theoretical biophysics and soft-condensed-matter physics at Simon Fraser University, Canada, his main interest was physics underlying DNA replication. He then moved on to study DNA segregation at the FOM–Institute AMOLF in Amsterdam for his first postdoctoral assignment, where he showed theoretically that replicating chromosomes in E. coli and other bacteria can segregate, driven by their conformational entropy. He then had a brief affair with evolution and moved to Paris to work in Miro Radman’s laboratory at L’Hospital Necker until he arrived at Harvard in 2007. His physical biology laboratory is trying to understand the extent to which basic physical principles governing the fundamental biological processes involving chromosomes during the cell cycle.

Nick Rhind studied math and biology as an undergraduate at Brown University and found the biology a lot easier. He went on to do his graduate work at U.C. Berkeley, working on the genetics of sex-determination in the round worm C. elegans. For his postdoctoral assignment, he moved to the Scripps Research Institute to study cell-cycle regulation in fission yeast with Paul Russell. There, he became interested in how and why cells regulate the cell cycle in response to DNA damage. He has continued with that line of research in his own laboratory at the University of Massachusetts Medical School, focusing recently on the regulation of DNA replication by DNA damage. This work has led to an interest in more general questions about the regulation of DNA replication and to a return to his mathematical roots.