Getting to the bottom of the heavy quark jet puzzle
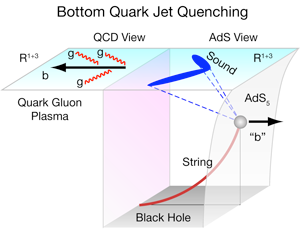
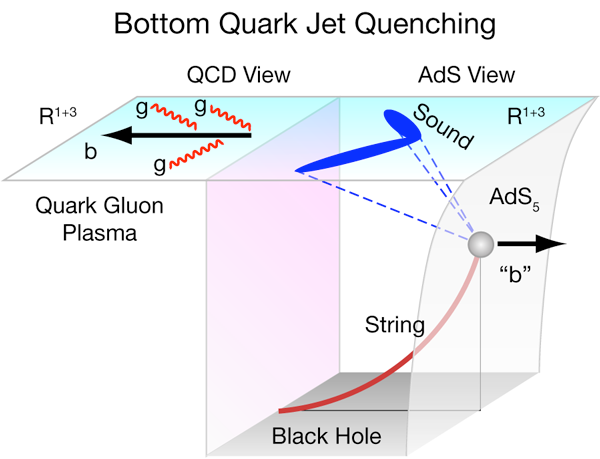
The experimental discovery [1] of a strongly coupled phase of quark-gluon plasma [2] produced in Au+Au reactions at 200GeV center-of-mass energy ( 100 times the sum of the nuclear rest mass) at the Relativistic Heavy Ion Collider (RHIC) has generated wide interest. This phase exhibits several key dynamical properties (in particular, minimally dissipative “perfect” fluidity, and high opacity and quenching of jets emitted in the collision) that have defied a satisfactory explanation in terms of dynamical models based on quantum chromodynamics (QCD) calculations carried out with perturbation theory—so far. This has led some theorists to seek explanations outside conventional QCD. String theorists, led by Maldacena and others [3] have jumped into a fifth dimensional “gedanken” black hole located in the depths of an anti-de Sitter gravity world to seek an alternate “holographic” (that is, a classical gravity) description of very strongly coupled supersymmetric gauge theories (see Fig.1).
One of the most surprising and unexpected properties of the strongly coupled quark-gluon plasma phase is the apparent very high opacity of the plasma to even the highest energy and very heavy bottom quark jets. Such jets are created in rare hard processes when the highly relativistic nuclei collide and they provide one of the important diagnostic tools for studying the plasma. Recently, as now reported in Physical Review C and elsewhere, a refined theory of QCD radiative energy loss has been developed by Magdalena Djordjevic, at Arkansas State University, US, and colleagues [4] that may help resolve, in part, the current heavy quark puzzle at RHIC within the QCD point of view without the need to jump into a five-dimensional anti-de Sitter black holes to get to the bottom of this problem. Color magnetic dynamical effects and finite size nonstatic coherence effects in perturbative quark-gluon plasmas were shown to be able to increase significantly the radiative energy loss of heavy quarks. More importantly, the energy loss of bottom quarks was found to increase by 10– 20% more than the energy loss of light quarks due to these effects.
The strongly coupled quark-gluon plasma produced in Au+Au reactions at RHIC/BNL (at 200GeV per nucleon) and soon Pb+Pb at LHC/CERN (at 5.5TeV per nucleon) exists for only about 10-23s and is produced in a cylindrical volume of transverse radius less than 10-12cm. Yet it appears to reach near perfect local equilibrium at temperatures around 300– 500MeV (a few 1012K) and flow as the most perfect fluid known—even less dissipative than superfluid liquid helium. From the asymptotically free QCD point of view, the quark-gluon phase was predicted over thirty years ago to exist as a novel deconfined, chiral symmetric, and approximately conformal invariant phase of QCD matter when temperatures exceed a critical temperature of approximately 200MeV. This phase differs drastically from the well studied lower temperature (less than critical) hot hadron resonance gas phase in which all the quarks and gluons are permanently confined into color-neutral hadrons and both the chiral and conformal symmetry of the QCD action are manifestly broken. Numerical nonperturbative lattice QCD calculations confirm that for temperatures above a few times the critical temperature, the pressure of a strongly coupled plasma differs by less than about 20% from that of an ideal gas of massless, deconfined quarks and gluons.
Two qualitatively different classes of observables have been used to probe the properties of the strongly coupled quark-gluon plasma: (1) “long” wavelength (low transverse momentum pT<∼1GeV) “soft” hadronic final fragment distributions and (2) “short” wavelength (high transverse momentum pT>10GeV) rare “hard” probes. The intermediate 1<pT<10GeV scale probes properties of the dynamics of confinement (or how hadrons form) and the simple observed quark counting rules provide independent evidence for the deconfinement of quarks in the plasma. The perfect fluidity property of the strongly coupled quark-gluon plasma was discovered via the first class of observations via elliptic flow patterns. Here, I concentrate only on the second class of hard observables that naturally splits into two further subclasses (2a) “light” quark/gluon/charm jets and (2b) “heavy” bottom quark (with mass around 4.5GeV) jets. Bottom quarks were originally thought to be more like bowling balls that should easily penetrate even the densest of strongly coupled quark-gluon plasmas. The surprising high attenuation of bottom jets observed at RHIC has caused a flury of theoretical activity and was an important factor motivating the recent work of Djordjevic [4].
The main idea of jet tomography [5,6] is to use the observed attenuation pattern (the nuclear modification of the Au+Au jet yield relative to appropriately scaled p+p jet yields) as a way to measure the energy loss per unit length as a function of jet energy, mass, and path length. This in turn gives information about the density and opacity of the plasma. Given a theory of quark energy loss, tomographic properties of the medium can be inferred similarly to how computer aided tomography with x rays or positrons are used routinely in medical applications to image density variations. Light quark and gluon jet quenching data have been used [6] to infer that the proper energy density of the strongly coupled plasma is initially about 100 times greater than in the center of neutron stars and ground-state nuclei in such high-energy collisions.
The initial flux of bottom quark jets can be experimentally calibrated in proton-proton reactions and checked against perturbative QCD theory. They are therefore independent and complementary hard probes of the plasma density. In addition, deuterium beam control experiments D+A→bˉb+X can be used to isolate and help to deconvolve initial state effects such as nuclear shadowing.
The successful test of the perturbative QCD theory prediction [5,6] of light jet quenching in central Au+Au and the predicted nonquenching of light jets in the control D+Au reaction convinced me in 2003 that the quark-gluon plasma is produced in almost every reaction at RHIC energies and that the short wavelength properties [item (2a) above] could be well described within perturbation theory. As a further test of the perturbative approach, Dokshitzer and Kharzeev predicted [7] that in contrast to light mass jets, heavy quark jets should exhibit a “dead cone” interference effect that suppresses induced gluon radiation within a range of angles. This should reduce the attenuation of bottom quarks relative to light mass jets. Djordjevic’s earlier work [8] generalized an earlier approach called the Gyulassy-Levai-Vitev (GLV) theory [6] to all orders in opacity theory for heavy quarks and predicted (in what is now called DGLV theory) that less than one half of the bottom quark jets should be absorbed by the plasma while most ( 75%) of the light mass jets should be absorbed.
However, the nonphotonic single electron data [9] from RHIC revealed that bottom quarks are attenuated almost as much as light quark/gluon/charm jets. The data indicated that about 70% of the produced bottom jets at pT∼10– 20GeV are also absorbed by the highly opaque strongly coupled quark-gluon plasma medium. Unlike in the bowling ball analogy predicted by perturbative QCD models, the experimental plasma acted more like a “black hole,” absorbing most of both light and heavy bottom jets. Our subsequent attempts to improve the theory [10,11] by including finite opacity fluctuations of elastic as well as inelastic energy loss and fluctuations of path lengths, reduced, but did not eliminate, discrepancy with the data.
In 2006, Gubser, and independently, Herzog et al. [12], proposed the novel string drag model illustrated in the right side of the figure as a specific realization of the conjectured AdS/CFT holography paradigm. In that picture, heavy quark jet propagation in a strongly coupled quark-gluon plasma is transformed into a “holographic” analog problem of a string moving through a ten-dimensional curved spacetime with one endpoint moving at a fixed height (the vertical thin line) in the fifth dimension. At rest, the heavy quark string hangs vertically down and its mass is fixed by its length times the string tension. When moving as a jet, the string stretches backwards above a three-dimensional flat black hole “brane” (the grey region in Fig.1). The black hole has entropy proportional to its higher dimensional horizon “area” with a corresponding Hawking temperature. It serves as an analog geometric model of the strongly coupled plasma. The supersonic string drag distorts the metric of the background AdS5×S5 geometry and the disturbance propagates (dashed lines) via gravitons to the upper flat Minkowski spacetime boundary, where experimentalists await to measure the hadronic and leptonic fragments from those energy stress ripples.
Heavy quark energy loss is predicted in the AdS approach to increase as the square root of the so called ‘t Hooft coupling constant ( λ=4παQCDNc). However, to justify AdS classical gravity approximation both limits, λ→∞ as well as Nc→∞, must be taken. Of course in this limit even a stampeding elephant could be stopped dead within 10-12cm. To our surprise [13], we found nevertheless that the holographic model can explain both hard class (2b) and soft class (1) quark-gluon plasma dynamical observables when the parameters of the AdS theory are downward extrapolated to a moderate and physically relevant number of colors Nc=3, for a coupling value of λ=g2Nc=12. Unfortunately, light quark and gluon jets are not so easily described in this holographic setup since their corresponding string description [14] remains very sensitive to uncertainties about the initial string shape and velocity distributions. In contrast, such highly virtual light mass jets and their final state quantum coherence can now be quantitatively described by QCD methods as in Djordjevic’s recent work [4].
Of course the impressive successes of the AdS holography approach do not exclude the possibility that sufficiently refined QCD techniques can be developed that can also explain the bottom jet data. Duality implies, after all, only an equivalence of descriptions, albeit in completely different conceptual terms and with different computational algorithms. It may be harder to work in one description than in the other in any particular situation or application, but both are supposed to account for the same physics. The recent work of Djordjevic [4] is an important step to test whether a suitable extrapolation of weak coupling methods, and upward toward stronger coupling dynamics, can reach the same level of compatibility with RHIC data as current downward extrapolations from the ultrastrong coupling AdS holography seems to achieve.
In a remarkable solo tour de force calculation, Djordjevic discovered a simple algebraic rule that could transform the solutions [8] of the static DGLV problem into new solutions [4] of the more complicated dynamical color magnetic scattering problem in finite size plasmas. The first numerical results reported in [4] are encouraging in that the magnetic effects tend to increase the heavy quark energy loss. The open question now is whether that increase is sufficiently large relative to the light quark energy loss to reproduce simultaneously both light and heavy jet quenching data within the same QCD approach. In a separate development, recent work by Vitev [15] identified additional possible hadron final state absorption channels that could further enhance the heavy quark energy loss relative to light jets.
While it is too early to tell which approach illustrated in Fig.1 will prove to be the most robust and useful, these and other developments suggest that it is prudent now to keep at least one foot out of the AdS black hole and rooted on the standard model side, while work continues to advance both theoretical approaches in order to get to the bottom of the heavy quark jet puzzle at RHIC.
Looking forward, the LHC/CERN will soon extend greatly the kinematic range and detector capabilities for identify heavy quark flavor tagged jet studies in ultrarelativistic nuclear collisions. This will enable new tests of both light and heavy quark jet dynamics [16,17] to help further discriminate between the QCD and AdS approaches to strongly coupled dynamics of quark-gluon plasmas.
References
- BNL -73847-2005 Formal Report; I. Arsene et al., Nucl. Phys. A 757, 1 (2005); B. B. Back et al. (PHOBOS Collaboration), ibid. 757, 28 (2005); J. Adams et al. (STAR Collaboration), 757, 102 (2005); K. Adcox et al. (PHENIX Collaboration), 757, 184 (2005); http://www.bnl.gov/rhic/newPhysics.asp.
- M. Gyulassy and L. McLerran, Nucl. Phys. A 750, 30 (2005)
- J. M. Maldacena, Adv. Theor. Math. Phys. 2, 231 (1998); Int. J. Theor. Phys. 38, 1113 (1999); E. Witten, Adv. Theor. Math. Phys. 2, 253 (1998); 2, 505 (1998); O. Aharony et al., Phys. Rep. 323, 183 (2000)
- M. Djordjevic, Phys. Rev. C 80, 064909 (2009); arXiv:0903.4591 (nucl-th); Nucl. Phys. A 830, 163C (2009); M. Djordjevic and U. W. Heinz, Phys. Rev. Lett. 101, 022302 (2008)
- M. Gyulassy and M. Plumer, Phys. Lett. B 243, 432 (1990); X. N. Wang and M. Gyulassy, Phys. Rev. Lett. 68, 1480 (1992)
- M. Gyulassy, P. Levai, and I. Vitev, Nucl. Phys. B 594, 371 (2001); I. Vitev and M. Gyulassy, Phys. Rev. Lett. 89, 252301 (2002); M. Guylassy, I. Vitev, X. N. Wang, and B. W. Zhang, in Quark Gluon Plasma 3, edited by R. C. Hwa and X. N. Wan (World Scientific, Singapore, 2003)[Amazon][WorldCat]
- Y. L. Dokshitzer and D. E. Kharzeev, Phys. Lett. B 519, 199 (2001)
- M. Djordjevic et al., Nucl. Phys. A 733, 265 (2004); Phys. Rev. Lett. 94, 112301 (2005)
- S. S. Adler et al. (PHENIX Collaboration), Phys. Rev. Lett. 96, 032301 (2006); ibid. 98, 172301 (2007); B. I. Abelev et al. (STAR Collaboration), Phys. Rev. Lett. 98, 192301 (2007)
- M. Djordjevic et al., Phys. Lett. B 632, 81 (2006)
- S. Wicks et al., Nucl. Phys. A 784, 426 (2007)
- S. S. Gubser, Phys. Rev. D 74, 126005 (2006); Nucl. Phys. A 830, 657C (2009); C. P. Herzog et al., JHEP 07, 013 (2006)
- J. Noronha, M. Gyulassy, and G. Torrieri, arXiv:0906.4099 (hep-ph)
- S. S. Gubser et al., JHEP 10, 052 (2008); P. M. Chesler et al., Phys. Rev. D 79, 125015 (2009)
- I. Vitev, J. Phys. G 35, 104011 (2008)
- W. A. Horowitz and M. Gyulassy, Phys. Lett. B 666, 320 (2008)
- B. Betz et al., Phys. Lett. B 675, 340 (2009)