A guided tour through the wild nuclear landscape

Gilad Perez

Viewpoint

A guided tour through the wild nuclear landscape

Department of Particle Physics, Weizmann Institute of Science, Rehovot 76100, Israel
and the C. N. Yang Institute for Theoretical Physics, Stony Brook University, Stony Brook, NY 11794-3840

March 16, 2009• Physics 2, 21

Study of variations in the mass and interactions of quarks may reveal whether fundamental constants are governed by “environmental selection rules” that lead to complex universes capable of having observers.

Figure caption — **Figure 1:** Graphical presentation of the parameter space examined by Jaffe, Jenkins, and Kimchij [11]: the triangle altitude corresponds to the sum of quark masses $m_{T} = Σ_{i} m_{i}$ . The quark mass is given by the perpendicular distance from the corresponding side. Our Universe corresponds to the point marked by the arrow on the middle triangle. The green (red) bands represent congenial (uncongenial) worlds and the white region requires further investigation.

Our Universe exhibits a remarkable degree of complexity. We find structures with typical scale of $10^{24}$ meters in the form of superclusters of galaxies all the way down to $10^{- 15}$ meters, the size of a proton. It seems magical that roughly 14 billion years ago, the Universe consisted of a soup of nearly structureless plasma, which later evolved into our rich observed surroundings. The story of our cosmological evolution legitimately deserves to be called a thriller: one can identify various microscopic parameters for which small variations would render a universe drastically different than the one we observe [1]. In many cases the modified Universe would be boring, possibly with a lifetime of a fraction of a second or just frozen and empty [2–7].

The most striking example for this cosmic fragility is related to the cosmological constant (or the present scale of the accelerated expansion of our Universe), $Λ_{CC}$ . In 1987 Weinberg [8] pointed out that the scale of the cosmological constant has to be tiny, roughly smaller than $10^{- 11}$ of the proton mass, or else no galaxies would have formed. Amazingly enough, the measured scale of $Λ_{CC}$ is only slightly smaller than this bound [9]. Thus, our cosmological chronicle is like a Hollywood blockbuster where at any instance the hero might die and the movie is terminated before the end of the first scene. Yet somehow we know that the hero will survive 90 minutes of danger. One may wonder whether a basic form of an environmental selection principle is at work here, where some fundamental parameters may only take values such that a complex enough universe—one capable of having observers—is formed [10].

Robert Jaffe, Alejandro Jenkins, and Itamar Kimchi of the Massachusetts Institute of Technology now report in Physical Review D [11] their investigation related to a precondition to the fascinating issue of whether an environmental selection mechanism exists. In essence, they analyze how different our world would be if the basic laws of physics and constants are varied. Their work tries to answer a naive “what would have happened if…” question. Make no mistake, this question regarding the consequences of changing our basic laws of nature, poses an extremely difficult scientific challenge. Addressing it allows us to look at our habitat from an unusual perspective, which undoubtedly offers a better understanding of our own world. As the physicist Freeman Dyson once put it [12], “The aim is to establish numerical bounds within which the destiny of the Universe must lie.”

One of the most challenging aspects of the task of identifying these environmental bounds is related to nuclear physics. Nuclear dynamics at finite temperature and pressure determines the element abundances in our Universe through big-bang nucleosynthesis (BBN), as well as the rate of production of heavy elements (of which our planet and we are made) in astrophysical environments. Furthermore, at zero temperature, nuclear interactions control the atomic and isotopic structure of our world, the basic input for chemistry. Thus, nuclear physics is a central building block from which structure and complexity stem. Jaffe et al. [11] focus on studying how the structure of elements is modified when the fundamental parameters—the light quark masses and the Quantum Chromodynamics (QCD) fundamental scale $Λ_{QCD}$ (which sets the confining scale of quarks and gluons within the nucleons)—are changed. Issues related to heavy element synthesis and BBN are not addressed and can be included as an additional set of constraints and parameters [3,4,7].

Naively, one might be surprised that nuclear dynamics has a strong sensitivity to the light quark masses. After all, the up and down quark masses are more than an order of magnitude below the scale of $Λ_{QCD} \sim 200 MeV$ and more than two orders of magnitude below the proton mass. However, the nuclear forces, spectrum, and binding energies are in general highly nontrivial functions of the QCD parameters. For instance, increasing the up-down quark mass difference by less than $10 MeV$ (that is, on the order of $1 %$ of the proton mass) would make hydrogen and its isotopes unstable [11].

In the analysis carried out by Jaffe et al. [11] cases satisfying the following requirements are fully considered: (i) only three light quarks, with masses below $Λ_{QCD}$ ; (ii) only two light, long-lived, baryons (analogous to the proton and neutron of our Universe); (iii) stable charge-one and charge-six nuclei (analogous to hydrogen and carbon). The rationale behind these conditions is that it would make organic chemistry possible (with these prior conditions, heavier elements like oxygen are also stable). Regions in parameter space that violate these rules are considered “uncongenial” by the authors.

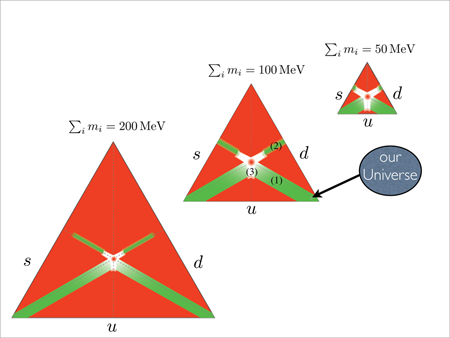
It is not obvious that uncongenial “universes” would be hostile to observers, but it is clear that these worlds will be drastically different than ours. The sum of light quark masses, $m_{T} = m_{u} + m_{d} + m_{s}$ , is varied together with $Λ_{QCD}$ such that the average mass of the two lightest baryons is held fixed to its observed value ( $940 MeV$ ). For a fixed value of $m_{T}$ , light quark masses may be represented by the points in the interior of an equilateral triangle with altitude of $m_{T}$ , as shown in Fig. 1. Quark masses are given by the perpendicular distance from the point to the corresponding triangle’s side. Since the quantum numbers of $s$ and $d$ are identical, we expect a left-right mirror symmetry for the congenial parameter space.

To test congeniality, for each point within the triangle, the authors evaluate the baryon spectrum and the corresponding nuclei structure. This is done by computing the baryon spectrum via $SU (3) (flavor = u, d, s)$ perturbation theory, and evaluating nuclear masses with two separate tools: For a nucleus made of two baryon species, similar to the ones in our Universe, the binding energy is estimated via simple extrapolation, whereas for heavy nuclei or nuclei made of more than two baryons, a semi-empirical mass formula is developed.

The masses of the ultralight mesons, our pions, strongly depend on the quark masses. This affects the binding energy in a way that is hard to evaluate. The authors argue that the dominant effect is due to a correlated two-pion exchange process, mediated via $f_{0}$ ( $600 MeV$ ) (also known as the elusive $σ$ particle), which induces the intermediate range attraction in the nucleon-nucleon force. Consequently, since the $f_{0}$ mass is roughly kept constant on each of the slices [13] the actual sensitivity of the resulting nuclear binding energy may be less dramatic than one might expect [2,6]. Hence, for universes that passed the requirements (i) and (ii) above, the main test is for the stability of nuclei against fission, strong particle emission (analogous to $α$ -decay), and weak nucleon emission.

We now turn to review the main conclusions. The cases that are considered are (a) one light quark leading to a single light baryon, (b) two light quarks with equal electric charge, (c) two light quarks with different charge, (d) one light quark leading to two light baryons, (e) three light quarks. The potentially congenial worlds can be divided into three categories: Type 1, the “neighborhood”—two light quarks with charges $2 / 3$ and $- 1 / 3$ with mass difference up to $30 MeV$ , with our own world lying comfortably away from the edges ( $m_{d} - m_{u} \sim 2 MeV$ ). Type 2, an “inverted hierarchy” with one light quark, charge $- 1 / 3$ , and two heavier, approximately degenerate quarks with charges $- 1 / 3$ and $2 / 3$ , the light nuclei being the analog of the neutron and the $Σ -$ . No other assignment of light quark charges yields congenial worlds with two baryons participating in nuclei. Type 3, the “baryonic zoo”—three or more baryon species form the nuclei building block, where congenial issues are discussed, but a full characterization of them is left for future investigation.

The results are summarized in Fig. 1. The green congeniality bands beginning at the corners belong to type 1. The bands beginning at the centers of edges are of type 2. White regions are of type 3, which, at present, belong to the congeniality limbo. (The numbers are shown on the middle triangle only.) The center of the triangle is red because it probably results in a world with only neutral nuclei, where a fantastically large number of nucleons is required to form a carbonlike atom.

The results of the paper draw a fascinating map of how nuclear dynamics responds to small and correlated deformations of the strength of the $QCD$ force and the light quark masses. We find that three issues are particularly interesting: First, most of the parameter space, scanned in the analysis, consists of universes that are drastically different from ours; second, a universe in which only a single quark is ultralight might not be very different from our own one; and third, a universe with three ultralight quarks seems to lead to a neutrophilic nuclear structure where electrons do not bind to the nucleus, and which is therefore likely to be hostile. Other issues are left for further investigation. The sum of quark masses, $m_{T}$ is bounded from below but the precise value is unknown. Similarly, when $m_{T}$ is increased one should expect several new effects to start being important (for example, higher order terms in $SU (3)$ flavor-breaking might matter, or a single pion exchange might dominates the binding dynamics) and the resulting nuclear structure is expected to be modified. Finally, we emphasize that additional interesting phenomena and constraints may arise once cosmological evolution is included. In particular, analysis of big-bang nucleosynthesis might change the congeniality map since congenial universes might be found to be nucleosynthesis-phobic.

Acknowledgments

The author thanks M. Karliner and R. L. Jaffe for help during the preparation of this article.

Note added (19 March 2009): After publication, the author became aware of related work in a paper by T. Damour and J. F. Donoghue [Phys. Rev. D 78, 014014 (2008)] which, based on recent work on nuclear binding, extend the anthropic constraints on the light quark masses.

References

B. Carter in Confrontation of Cosmological Theories with Observation, edited by M. S. Longair (Reidel, Dordrecht, 1974); J. D. Barrow and F. J. Tipler, The Anthropic Cosmological Principle (Oxford, 1986) [Amazon][WorldCat]; F. Hoyle, D. N. F. Dunbar, W. A. Wenzel, and W. Whaling, Phys. Rev. 92, 649 (1953); A. D. Sakharov, Sov. Phys. JETP 60, 214 (1984) Zh. Eksp. Teor. Fiz. 87, 375 (1984); B. J. Carr and M. J. Rees, Nature 278 605 (1979)
C. J. Hogan, Rev. Mod. Phys. 72, 1149 (2000); arXiv:astro-ph/9909295
M. Tegmark, A. Aguirre, M. Rees, and F. Wilczek, Phys. Rev. D 73, 023505 (2006); arXiv:astro-ph/0511774; M. Tegmark and M. J. Rees, Astrophys. J. 499, 526 (1998); arXiv:astro-ph/9709058; A. Aguirre, Phys. Rev. D 64, 083508 (2001); arXiv:astro-ph/0106143; S. Hellerman and J. Walcher, Phys. Rev. D 72, 123520 (2005); arXiv:hep-th/0508161; M. L. Graesser, S. D. H. Hsu, A. Jenkins, and M. B. Wise, Phys. Lett. B 600, 15 (2004); arXiv:hep-th/0407174; B. Feldstein, L. J. Hall, and T. Watari, Phys. Rev. D 72, 123506 (2005); arXiv:hep-th/0506235
R. Harnik, G. D. Kribs, and G. Perez, Phys. Rev. D 74, 035006 (2006); arXiv:hep-ph/0604027
L. J. Hall and Y. Nomura, Phys. Rev. D 78, 035001 (2008); arXiv:0712.2454; R. Bousso, L. J. Hall, and Y. Nomura, arXiv:0902.2263
V. Agrawal, S. M. Barr, J. F. Donoghue, and D. Seckel, Phys. Rev. Lett. 80, 1822 (1998); arXiv:hep-ph/9801253; Phys. Rev. D 57, 5480 (1998); arXiv:hep-ph/9707380
J. Hogan, Phys. Rev. D 74, 123514 (2006); arXiv:astro-ph/0602104
Weinberg, Phys. Rev. Lett 59, 2067 (1987)
G. Riess et al., (Supernova Search Team Collaboration), Astron. J. 116, 1009 (1998); arXiv:astro-ph/9805201; S. Perlmutter et al., (Supernova Cosmology Project Collaboration), Astrophys. J. 517, 565 (1999); arXiv:astro-ph/9812133
See, e.g., A. Vilenkin, Phys. Rev. Lett. 74, 846 (1995); arXiv:gr-qc/9406010; G. Efstathiou, Mon. Not. Roy. Astron. Soc. 274, L73 (1995); R. Bousso, Phys. Rev. Lett. 97, 191302 (2006); arXiv:hep-th/0605263; R. Bousso, Phys. Rev. Lett. 97, 191302 (2006); arXiv:hep-th/0605263; J. Garriga, M. Livio, and A. Vilenkin, Phys. Rev. D 61, 023503 (2000); arXiv:astro-ph/9906210; A. Vilenkin, arXiv:astro-ph/0407586; A. De Simone, A. H. Guth, M. P. Salem, and A. Vilenkin, Phys. Rev. D 78, 063520 (2008); arXiv:0805.2173; A. Linde, JCAP 01, 022 (2007); arXiv:hep-th/0611043
R. L. Jaffe, A. Jenkins, and I. Kimchi, Phys. Rev. D 79, 065014 (2009)
F. J. Dyson, Rev. Mod. Phys. 51, 447 (1979)
C. Hanhart, J. R. Pelaez, and G. Rios, Phys. Rev. Lett. 100, 152001 (2008); arXiv:0801.2871

About the Author

Gilad Perez received his Ph.D. from the Weizmann Institute of Science in 2003. He was a postdoctoral fellow at Lawrence Berkeley National Laboratory. He joined the faculty of the C. N. Yang Institute for Theoretical Physics at Stony Brook University in 2006 and the Weizmann Institute in 2008. Gilad’s research concerns study of models beyond the standard model of fundamental particle interactions and their experimental implications in astrophysics and colliders.