Order out of noise

Fabio Marchesoni

Viewpoint

Order out of noise

Dipartimento di Fisica, Università di Camerino, I-62032 Camerino, Italy

March 23, 2009• Physics 2, 23

Stochastic resonance, in which a periodic signal applied to a nonlinear system can be amplified by adding noise, has been observed in a mechanical system and predicted to occur in a Bose-Einstein condensate.

Figure caption — **Figure 1:** The torsional oscillator used to study optomechanical stochastic resonance. A gold-coated glass plate is suspended from a tungsten wire, and a laser reflected from the center point indicates the deflection of the plate, while feedback electrodes are used to drive the oscillator dynamics. A mirror fastened to the end of the plate forms an optical cavity with a second laser, which couples the oscillator to a multiwell potential created by radiation pressure. The optical cavity thus causes the resulting torsion arm to pop into one of several positions. A weak noisy signal applied to the electrodes yields an enhanced deflection signal via the stochastic resonance effect if the noise amplitude is in the right range. (Adapted from Mueller *et al.* [4].)

Thirty years ago climatologists asked their physicist friends to explain the almost periodic occurrence of the ice ages, or how a small change of one parameter out of many in the Earth orbit around the Sun can cause a shift of the climate as dramatic as the ice ages. Although not entirely applicable to the problem at hand, the physicists’ puzzling response was thought-provoking [1]. Climate supports two stable states, one at a lower temperature (an ice age) and one at a higher temperature (and let’s forget global warming issues, for the moment); fluctuations attributable to geodynamical events can cause random transitions between those two states. The external small, periodic modulations of the Earth orbit bias the random transitions towards times where such transitions are the most likely. If the fluctuations are too small, the transitions occur too infrequently and out of tune with a given modulation of the Earth orbit; if the fluctuations are too large, the random transitions would be too frequent and, therefore, also out of tune. Hence, at an optimal amplitude of the fluctuation, depending on the modulation frequency [2], periodic transitions can be driven by random noise, a phenomenon known as stochastic resonance.

Although the idea was brilliant, subsequent data did not support the physicists’ explanation for the ice ages. But this was not the end of stochastic resonance. Quite the contrary, the concept of stochastic resonance grew into a new (and at times abused) paradigm, which changed the way we now perceive noise in the natural and social sciences [3]. What triggered scholars’ curiosity the most was the suggestion that noise, a nuisance when you tried to tune in an old radio or TV set, can actually be used to optimize the operation of a variety of systems, ranging from simple physical devices to complex networks of intelligent agents.

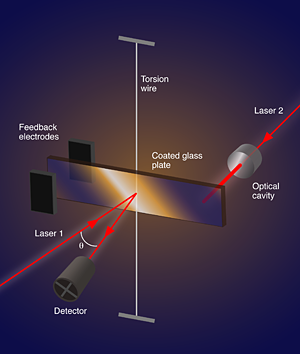
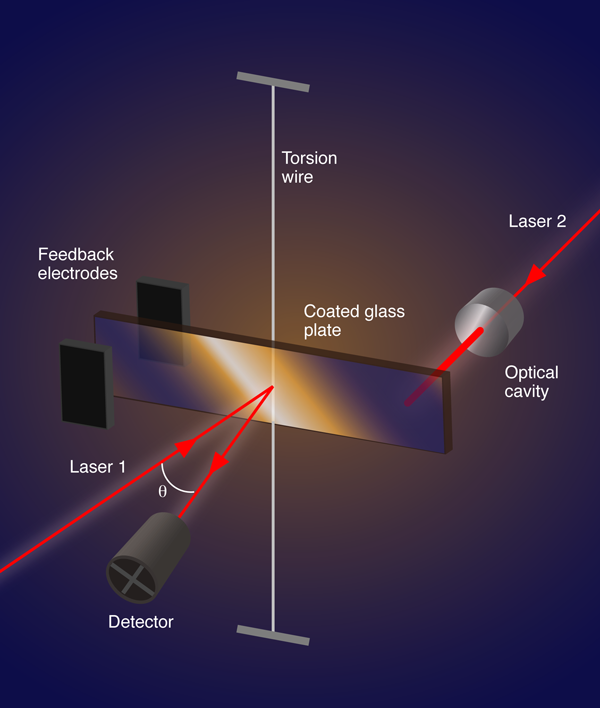
In a paper [4] appearing in Physical Review A, F. Mueller, S. Heugel, and L. J. Wang, at the Max Planck Institute for the Science of Light, Erlangen, Germany, have reported experimental evidence of stochastic resonance in a macroscopic mechanical oscillator, obtained by coupling a linear torsion pendulum to an optical cavity (see Fig. 1). The resulting optomechanical potential is multistable and strongly asymmetric. By feeding an optimal level of white noise to the torsion balance, they succeeded in enhancing the oscillator sensitivity to low-frequency external forces as weak as a few tens of femtonewtons. Such an optomechanical oscillator is likely to prove useful in the technology of gravitational wave interferometers, like LIGO in the USA and VIRGO in Europe, where we are interested in testing new materials for the suspension of optical elements at extremely low frequencies and for detection of vanishingly small forcing amplitudes. The accuracy reached by these experimenters working with a macroscopic oscillator is no less remarkable than that reported for bistable nanomechanical silicon oscillators [5], where stochastic resonance was also observed.

Another group recently explored the possibilities of stochastic resonance in mechanical systems. In a paper that recently appeared in Physical Review Letters [6], F. Cottone, H. Vocca, and L. Gammaitoni, at the University of Perugia, Italy, have implemented the stochastic resonance mechanism to amplify the response of nonlinear oscillators to external mechanical fluctuations, thus outperforming standard linear electromechanical energy converters. Their experiment demonstrates a new, more efficient way of harvesting ambient vibrational energy to power mobile electronic devices at the submillimeter scale (MEMS).

Stochastic resonance can occur in completely different systems as well. In a paper appearing in Physical Review A [7], three theorists, D. Witthaut (Niels Bohr Institute, Copenhagen Denmark), F. Trimborn (Technische Universität, Braunschweig, Germany), and S. Wimberger (Universität Heidelberg, Germany), suggest that the coherence properties of a Bose-Einstein condensate in a double-well trap can be enhanced by tuning the system to an optimal dissipation. More importantly, the interplay of interaction and dissipation can drive the condensate to a state of maximum coherence, while either process alone would lead to a loss of coherence. The observation of stochastic resonance in the absence of an external periodic modulation is a typical quantum-mechanical effect, which is built into the Bloch equations that describe (in the rotating wave approximation) spins driven by an external field. The computational evidence reported by these authors is so compelling that I expect an experimental demonstration of this effect to follow soon.

The physical and methodological settings of these recent articles look so far apart that the reader might be left wondering if stochastic resonance has been oversold as a buzzword for any and, possibly, unrelated manifestations of the constructive role of fluctuations and dissipation. As a matter of fact, from its early inception in the 1980s stochastic resonance has evolved into a rather sophisticated paradigm, where the three original ingredients, noise, bistability (or some sort of a threshold), and periodic modulation, have been and still are the subject of deep elaboration.

A crucial turning point in the history of stochastic resonance occurred with the first attempts to apply the new mechanism to biological matter [3]. Noticing the resemblance between escape-time distributions in a weakly rocked bistable system and the interspike interval distributions of neuronal action potentials was a first step. Proving that externally added noise does enhance the performance of sensory nerves in invertebrates established stochastic resonance as a respected tool of biological physics. These first observations inspired the visionary idea that biological systems may have evolved to perform best under ambient noise levels—the ultimate criterion of Darwinian evolution, and a far cry from the pessimistic implications of Boltzmann’s $H$ theorem and its relentless increase in entropy. The attention of investigators thus focused on the role of intrinsic noise in the cell, i.e., thermal fluctuations that become appreciable because the engines of life are small and made of relatively few constituents. In fact, although Nature had evolved to a state that operates optimally under ambient noise levels, the sources of microscopic noise must be regarded as intrinsic. Despite much effort, the reported evidence of stochastic resonance in periodically gated cellular ion channels, the elementary building blocks of neuronal machinery, is far from being conclusive. The quest for the smoking gun proving that evolution continuously adjusts to unavoidable and ever-changing ambient fluctuations is still being pursued.

Many of the applications of stochastic resonance, in particular to neuroscience, are concerned with large ensembles of coupled constituent systems. Neurons are coupled chemically through synapses and electrically through gap junctions, and thus form large networks. Such a network can exhibit behaviors that are drastically different from those of its constituents. From neurophysiology we learn that the coexistence of two or more stable states, or transition thresholds, and internal dissipation can thus emerge as collective effects, depending on coupling and coupling topology, that is, the coupling between the torsion pendulum and the measurement apparatus in the experiment of Mueller et al. [4].

Early applications [3] of stochastic resonance to nonlinear and dynamical systems made use of drives that possess more complex spectra, as is also the case in many real situations, such as multiharmonic signals and aperiodic signals with a finite bandwidth centered on a dominant frequency. Belonging to the latter category is the case of a bistable dimer traveling on a spatially periodic substrate. The time sequence of the noise-induced switches between the two stable dimer configurations becomes the most ordered for an optimal translational velocity of the dimer itself, a situation reminiscent of the spontaneous stochastic resonance phenomenon reported by Witthaut et al. [7].

As the literature on stochastic resonance keeps growing at a staggering rate [8], concerned colleagues often ask if we really need to advocate stochastic resonance any time an optimal amount of noise is required. It’s a fair question: after all, the positive role of noise as a lubricant is well established and so is its negative garbling effect on data transmission. The answer is no. For instance, an optimal combination of noise, periodic drives, and arrays of activation thresholds is also the basic recipe of noise-controlled rectifiers, known as Brownian motors [9]. But that is a totally different story.

I now come full circle, returning to the physicists’ answer to the ice age problem. Was that answer scholarly and brilliant, perhaps lucky, but really of no practical use in climate theory? While the big ice ages are thought to occur every $10^{5}$ years, during the glacial times sudden warmer periods occur more or less periodically at a rate of about 1500 years (the Dansgaard-Oeschger events). The analysis of Greenland ice-core data revealed a distribution of such event times, which turned out to be consistent with a stochastic resonance model of the North Atlantic climate [10,11]. Moreover, the conclusion that such climate switches can be extremely rapid (less than 5 years) is a new important element to be considered in evaluating the impact of human activities on global warming.

References

R. Benzi, S, Sutera, and A. Vulpiani, J. Phys. A 14, L453 (1981); C. Nicolis and G. Nicolis, Tellus 33, 225 (1981); R. Benzi, G. Parisi, A. Sutera, and A. Vulpiani, 34, 10 (1982)
L. Gammaitoni, F. Marchesoni, and S. Santucci, Phys. Rev. Lett. 74, 1052 (1995)
For a review see, L. Gammaitoni, P. Hänggi, P. Jung, and F. Marchesoni, Rev. Mod. Phys. 70, 223 (1998)
F. Mueller, S. Heugel, and L. J. Wang, Phys. Rev. A 79, 031804 (2009)
R. L. Badzey and P. Mohanty, Nature 437, 995 (2005)
F. Cottone, H. Vocca, and L. Gammaitoni, Phys. Rev. Lett. 102, 080601 (2009)
D. Witthaut, F. Trimborn, and S. Wimberger, Phys. Rev. A 79, 033621 (2009)
For an update see, Topical issue on Stochastic Resonance, edited by L. Gammaitoni, P. Hänggi, P. Jung, and F. Marchesoni, Eur. Phys. J. B (to be published)
F. Marchesoni and P. Hänggi, Rev. Mod. Phys. (to be published); arXiv:0807.1283
B. Alley, S. Anandakrishnan, and P. Jung, Paleoceanography 16, 190 (2001)
H. Braun et al., Nature 438, 208 (2005)

About the Author

A graduate of the University of Pisa (Italy), Fabio Marchesoni specializes in areas of nonequilibrium statistical physics including stochastic processes, self-organized criticality, and stochastic resonance. He is co-founder of the VIRGO project, a French-Italian collaboration for the detection of gravitational waves, and has appointments at RIKEN (Japan) and Loughborough University (UK). He is a Fellow of the American Physical Society (2003), the Institute of Physics (IoP, 2004), and the American Association for Advancement of Science (2008), and was named an APS Outstanding Referee (2007). The author is presently professor of physics at the University of Camerino.