Electron crystallites floating on superfluid helium

François Peeters

Viewpoint

Electron crystallites floating on superfluid helium

Department of Physics, University of Antwerp, B-2020 Antwerp, Belgium

January 12, 2009• Physics 2, 4

Crystalline structures have been observed in nanoislands of electrons floating above superfluid helium. The energy required to add or subtract an electron from these quantum-dot-like islands agrees well with theory.

Figure caption — **Figure 1:** A series of Wigner crystal structures showing the arrangement of electrons in a circular island from an occupation number of $N = 3$ to $N = 100$ . The electrons form ring structures as more electrons are added. At $N = 15$ an inner ring of five electrons is formed, but at $N = 16$ the additional electron is forced to the center to start a new ring. For large $N$ , a triangular Wigner lattice forms in the center, while the outer electrons remain in rings.

When the temperature of a collection of particles is reduced, the kinetic energy will decrease relative to the average potential energy, and correlations between the particles will dictate the many-particle structure. A well-known example is the freezing of atoms or molecules into an ordered crystal phase, e.g., water molecules that crystallize into ice at a temperature of zero degrees Celsius. In 1934, Eugene Wigner, a theorist at Princeton University, made the bold prediction that electrons in a metal would undergo a similar transition to an ordered crystal phase [1]. Such a “Wigner crystal” was never observed in a metal. However, such structures can be observed in other environments and compared in detail with theory, as reported in Physical Review B [2] by Emmanuel Rousseau, Dmitri Ponarin, Likourgos Hristakos, Olivier Avenel, Eric Varoquaux, and Yuri Mukharsky at the Service de Physique de l’État Condensé Centre, Saclay, France.

To overcome the obstacles of trying to observe Wigner structures in metals, scientists in the 1970s constructed a new system where electrons were collected above the surface of liquid helium [3]. Using electrostatic fields and the tiny polarization of the helium, they were able to force the electrons into a two-dimensional layer with only vacuum between the electrons. This system became a model system for physicists because the interaction between the electrons is completely known and the kinetic energy is simply the one of free electrons in vacuum.

With this configuration, Grimes and Adams at Bell Laboratories showed in the late 1970s that when temperature was decreased below some specific value (which increases with the electron density) the electrons would form a strongly correlated state and fall into a triangular crystal lattice arrangement [4]. In contrast to crystals we encounter in daily life, in which the atoms or molecules attract each other, the electrons in a Wigner crystal are ordered due to their Coulomb repulsion. In typical crystals the distances between the atoms are typically on the order of angstroms (1 angstrom equals $0.1 nm$ ) while in an electron crystal this distance is a few thousand times larger. In the 1980s an alternative way to realize a Wigner crystal in a semiconductor heterostructure was demonstrated [5], based on the quenching of the kinetic energy by applying a large magnetic field, i.e., the electrons are forced into an orbiting state in which they all have the same kinetic energy and zero average translational energy.

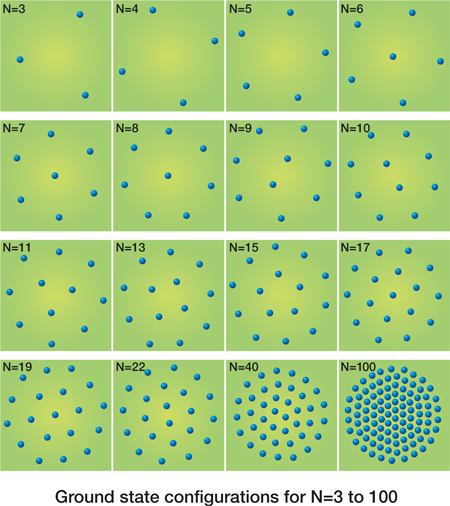
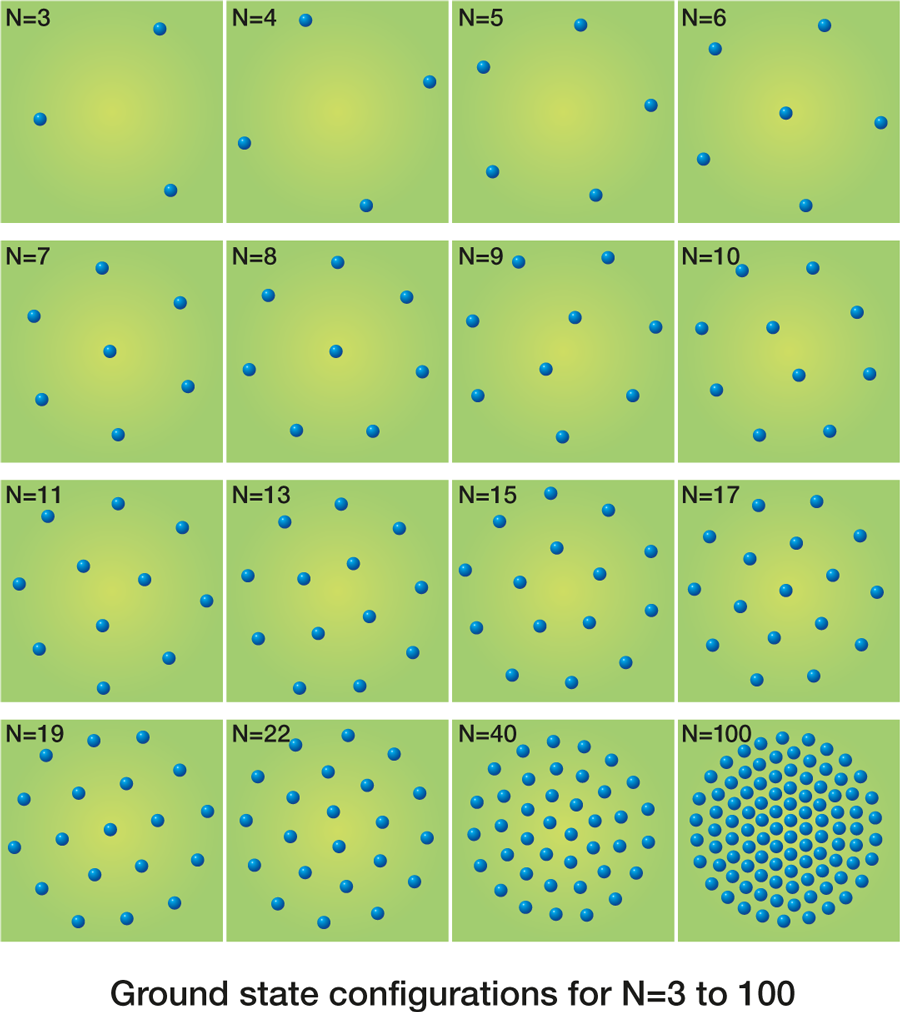
In the 1990s at the University of Antwerp, Bedanov and I investigated theoretically how such a Wigner crystal would be modified if it consists of only a small number of electrons restricted to a small circular area in space [6]. We found that the electrons arrange themselves in ring configurations and the inner shell consists of at most five electrons (Fig. 1). If an additional electron is added on the inner ring it is forced to the center and starts to act as a nucleation center for a new ring. We also constructed a Mendeleyev table for such electron arrangements, which have been called Wigner molecules, Wigner islands, or artificial atoms. If there is a large number of electrons (typically more than 100) the Wigner crystal is recovered in the center of the island while at the edge the electrons are arranged in rings. The electrons in the outer rings were found to be ordered in a circular deformed triangular lattice. If the last three rings are cut open and allowed to relax into a straight line, a one-dimensional Wigner lattice is found.

Up to now such ring arrangements in restricted geometries were observed only for large composite particles, such as colloidal particles in a liquid environment or in dusty plasmas, millimeter-size charged metallic balls, vortices in a mesoscopic superconducting disk, and in rotating liquid helium. In these systems the particles are “big,” typically of micrometer size or larger, and direct (visual) observation of the ordered particles was possible.

Rousseau et al. have now presented the first experimental evidence of Wigner islands of electrons formed on top of liquid helium [2]. In these experiments electrons were injected from a hot filament and trapped above a liquid helium surface. Those electrons float about 100 angstroms above the superfluid helium surface in vacuum. This is as good an ideal system as one is able to realize, because unlike solids, there are no impurities or defects present and there is also no underlying atomic lattice, which would limit the mobility of the electrons. A ring-shaped electrode was positioned below the helium surface, which traps the electrons laterally and through which the size of the island could be varied continuously. A single-electron transistor was positioned at the center of the trap to detect the charge in the island. The island was connected by a narrow channel to a reservoir of electrons through which single electrons could be shuttled between the island and the reservoir.

Because electrons are so tiny they cannot be directly visualized and therefore the geometrical arrangement of the electrons in the island had to be deduced indirectly from such properties as their escape energy (i.e., ionization energy) from the island or the energy required to add a single electron to the island (the addition energy). It has been shown that these energies depend on the ordered state of the electrons. In particular, the addition energy is equal to the difference in electrochemical potential between islands with $N$ and $N + 1$ electrons. From the experimental observed addition spectrum and detailed numerical simulations, information was obtained about the ground-state energy of the many-electron system in the island, which provided information on whether or not the electrons were spatially ordered.

The authors compared the experimental results with Monte Carlo simulations to confirm that they were in fact seeing the expected Wigner structures. Such results suggest that the electrons are radially ordered into shells but not orientationally locked, i.e., the shells can rotate with respect to each other. Although the agreement is satisfactory, questions about the heating of the electron island by the single-electron transistor (i.e., the charge detector) still need to be tackled. Future experiments might achieve lower temperatures by means of a reduction of the noise energy, opening up the possibility for a more detailed study of such Wigner islands and in particular of orientational order.

References

E. Wigner, Phys. Rev. 46, 1002 (1934)
E. Rousseau, D. Ponarin, L. Hristakos, O. Avenel, E. Varoquaux, and Yu. Mukharsky, Phys. Rev. B 79, 045406 (2009)
R. S. Crandall and R. Williams, Phys. Lett. 34A, 404 (1971)
C. C. Grimes and G. Adams, Phys. Rev. Lett. 42, 795 (1979)
E. Y. Andrei, G. Deville, D. C. Glatti, F. I. Williams, E. Paris, and B. Etienne, Phys. Rev. Lett. 60, 2765 (1988)
V. M. Bedanov and F. M. Peeters, Phys. Rev. B 49, 2667 (1994)

About the Author

François Peeters obtained his Ph.D. in 1982 at the University of Antwerp. Subsequently, he was a postdoctoral fellow at Bell Laboratories and Bellcore (New Jersey, USA). His research interests include the theory of semiconductor and superconductor nanostructures, Wigner crystallization of bilayers and wires, and quantum confinement in nanosize superconductors. He is a member of the Editorial board of Physica B, Journal of Nanoscience and Nanotechnology, Microelectronics Journal, and Solid State Communications. Peeters is head of the research group “Condensed Matter Theory” at the University of Antwerp. He is a fellow of the American Physical Society and was recently elected by the editors of the APS journals as an “outstanding referee.”