Lending an iron hand to spintronics

Piers Coleman

Viewpoint

Lending an iron hand to spintronics

Department of Physics and Astronomy, Rutgers University, 136 Frelinghuysen Road, Piscataway, NJ 08854-8019, USA

January 20, 2009• Physics 2, 6

The presence of iron in gold has long been known to lead to an increase in gold’s low-temperature resistivity. Theorists argue that this “Kondo effect” may have implications for spintronics as well.

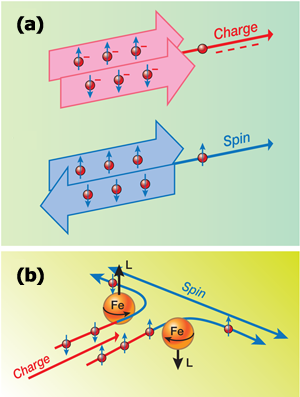
Figure caption — **Figure 1:** (a) In a charge current, spin “up” and “down” electrons flow together. In a spin current, up and down electrons flow in opposite directions. (b) A schematic of the spin Hall effect. Spin-orbit coupling induces an orbital motion opposite in direction to the electron spin, deflecting up- and down-spin electrons in opposite directions. The net effect is a conversion of charge into spin currents.

As semiconductor electronics push up against the limits of Moore’s law, physicists are seeking new ways to manipulate and store information in matter. A promising new direction is “spintronics” [1], a kind of electronics built around the spin carried by electrons, rather than the charge. Spin is the basis of ferromagnets, which are magnets in which the electron spins are aligned. The information bits on a hard drive are stored in tiny ferromagnetic domains, but a conventional electron current is a poor tool for manipulating magnetic information. Instead, spintronics offer the hope of reading and manipulating magnetic memory on microscopic scales through the control of pure spin currents, in which compensating currents of electrons with spin “up” and “down’” move in opposite directions [Fig. 1(a)].

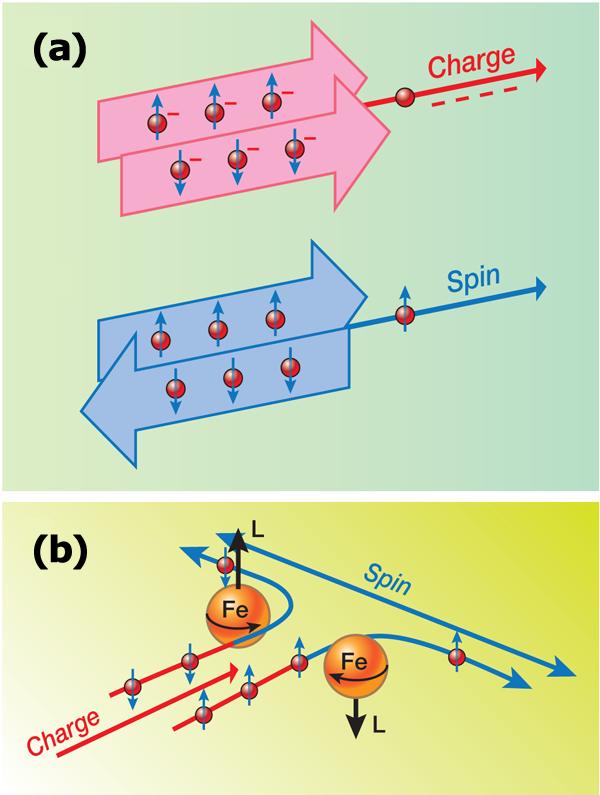
A dream of spintronics is to find a way to easily convert between spin and charge currents, a task many believe will involve tapping into (so far) unutilized quantum properties of matter. One such property is the “spin Hall effect” [2,3], whereby a charge current passing through a material converts into a spin current that moves in a perpendicular direction. This effect is a result of the spin-orbit interaction, which tends to align the spin ( $S$ ) and the orbital angular momentum ( $L$ ) of electrons in opposite directions [Fig. 1(b)]. When a spin-up electron scatters off an atom with strong spin-orbit coupling, it acquires a down-pointing angular momentum, which tends to twist its direction of motion around the atom and divert it off to the right. When a down electron scatters off the same type of atom, it tends to twist off to the left. The combined twisting or “skew scattering” action of spin-orbit coupling thus causes currents of up and down electrons to deflect in opposite directions, and the net effect is to produce a transverse spin current. This is the spin Hall effect. The inverse of this same effect converts a spin current into a transverse charge current. (Note that if the current is spin polarized, there will be more electrons moving in one perpendicular direction than the other, resulting in an actual transverse charge current, also called an anomalous Hall current.) This effect is presumed to be present in all nonmagnetic metals and semiconductors, but in all cases where it has been observed, it is too weak for applications.

A year ago, Takeshi Seki and colleagues at Tohoku University in Japan announced the surprise discovery of a “giant spin Hall effect” in ordinary gold [4]. When they injected a spin-polarized current into the gold, a large transverse Hall voltage developed, one or two orders of magnitude greater than the comparable effect in other heavy metals where the spin-orbit effect is large, such as platinum. Now, in a paper appearing in Physical Review Letters, Guang-Yu Guo, Sadamichi Maekawa, and Naoto Nagaosa [5] propose an intriguing theory for this giant spin Hall effect. Essentially, they argue that the effect is driven by electrons that scatter off iron impurities in the gold.

Magnetic iron impurities have long been known to have a large effect on the low-temperature resistivity of gold, via a mechanism called the Kondo effect. If Guo and collaborators are right in their interpretation, the observation of a giant spin Hall effect resulting from the Kondo effect will add a curious new twist to this story. The history of the Kondo effect stretches back over seventy-five years. In 1934, experimentalists in Leiden [6] found that as gold was cooled, its resistivity reached a minimum, and then started to rise again. It took three decades of improvement in sample quality before the mysterious effect was identified as a consequence of magnetic iron impurities. In 1963, Jun Kondo showed how multiple scattering of electrons off such magnetic impurities gives rise to a growth in resistivity at low temperatures [7,8]. Kondo demonstrated that below a certain temperature, now called the “Kondo temperature,” this magnetic scattering becomes so strong that the perturbation methods he was using broke down. His work opened up a heroic era of discovery in many-body physics. Today we know how to follow the physics of the Kondo effect below the Kondo temperature. Qualitatively, the Kondo effect describes how, at low temperatures, the surrounding electron sea dissolves the spin of the local moment associated with the iron so that it becomes delocalized. All that remains of strong magnetic scattering is a narrow “Kondo resonance” in the Fermi sea, which elastically scatters electrons near the Fermi energy and creates a great deal of resistance. It is this effect that drives the low-temperature upturn in resistance that made Kondo famous.

When a Kondo resonance combines with spin-orbit scattering, it gives rise to skew scattering effects, whereby up electrons are scattered in the opposite transverse direction to down electrons. When the electron current is polarized, this effect gives rise to a net transverse electron current, or anomalous Hall effect. This effect was first studied over twenty years ago by Albert Fert and Olivier Jaoul [9], and later, in the context of rare-earth atoms, by myself, Tiruppattur Ramakrishnan, and Philip W. Anderson [10]. What no one appreciated at the time, is that this same effect continues in the absence of an applied magnetic field, producing a spin Hall effect. It is the spintronics aspect of skew scattering that Guo et al. emphasize and bring out in their new paper. They propose that it is the same resonant skew scattering effect off iron impurities that is responsible for the large spin Hall effect in gold.

Despite its long history, the detailed Kondo physics of iron remains a controversial subject, in part because of the complex orbital structure of the impurity atom. The magnetism of iron in gold is carried by iron’s five valence $d$ electrons, each of which resides in one of five different $d$ orbitals. On an isolated $Fe$ atom, these $d$ orbitals are nearly degenerate, but in the cubic environment of the gold crystal, the $d$ orbitals split up into two components—a doublet, labeled the $e_{g}$ orbitals, and a triplet, labeled the $t_{2 g}$ orbitals. During the past year, both Guo et al. and a research collaboration of Theo Costi, Achim Rosch, and coworkers [11] have independently proposed that the Kondo effect in iron is “orbitally selective,” involving two widely different Kondo temperatures—one for each set of orbitals. Both groups suggest that some of the iron $d$ -spins delocalize because of the Kondo effect at room temperature, leaving behind two or three remaining electrons that only delocalize around 1 K.

Guo et al. propose that the electrons in the $t_{2 g}$ orbital of iron undergo a Kondo effect at high temperatures and argue that the residual resonant scattering drives a giant spin Hall effect. In their calculations, they find the effect of Coulomb interactions and spin-orbit coupling on the $t_{2 g}$ orbitals gives rise to a large orbital magnetic moment. By estimating the scattering phase shifts for resonant electron scattering off these orbital moments, Guo et al. predict they will undergo a large skew scattering effect that is responsible for the giant spin Hall effect. At present, unfortunately, the final estimate of the spin Hall effect by Guo et al. is very qualitative and awaits a more detailed theoretical formulation.

In a rival view of the Kondo effect in iron, Costi et al. propose that it is electrons in the $e_{g}$ orbital that have a high Kondo temperature, leaving behind $t_{2 g}$ $d$ electrons to undergo a low-temperature Kondo effect. In their model, iron does not have a large orbital magnetic moment, and the resonant scattering off $e_{g}$ orbitals is not expected to produce a large spin Hall effect.

This is a fascinating state of affairs—a wonderful example of the synergy that is possible between electronics applications and condensed-matter physics. If Guo et al. are right, the spin Hall conductivity of gold should scale with the iron concentration, moreover, one might expect iron atoms to produce a large anomalous Hall effect. This could be a very exciting and unexpected turn in the long-standing story of the Kondo effect of iron in gold. Potentially, our picture of iron in copper is also in for a major revision. In principle, the skew scattering mechanism for a giant spin Hall effect should be even stronger for rare-earth impurities, rather than transition-metal impurities, and the authors emphasize that this may be a very promising area for future experiments.

References

S. A. Wolf et al., Science 294, 1488 (2001)
M. I. Dyakonov and V. I. Perel, Sov. Phys. Solid State 13, 3023 (1972)
J. E. Hirsch, Phys. Rev. Lett. 83, 1834 (1999)
T. Seki et al., Nature Mater. 7, 125 (2008)
G-Y. Guo, S. Maekawa, and N. Nagaosa, Phys. Rev. Lett. 102, 036401 (2009)
W. J. de Haas, J. W. de Boer, and G. J. van den Berg, Physica 1, 1115 (1934)
J. Kondo, Prog. Theor. Phys. 32, 37 (1964); 27, 772 (1962)
P. Coleman, Ann. Henri Poincaré Suppl. 2, S559 (2003)
A. Fert and O. Jaoul, Phys. Rev. Lett. 28, 303 (1972)
P. Coleman, P. W. Anderson, and T. V. Ramakrishnan, Phys. Rev. Lett. 55, 414 (1985)
T. A. Costi , “Kondo decoherence: finding the right spin model for iron impurities in gold and silver,'' Phys. Rev. Lett. (to be published); arXiv:0810.1771

About the Author

Piers Coleman is a Professor of Physics at the Serin Laboratory, Rutgers University, a graduate of Cambridge and Princeton Universities, and a former fellow of Trinity College, Cambridge. He is particularly interested in strongly correlated electron systems, particularly involving the intersection of magnetic and superconducting behavior. “Condensed-matter physics is not only an applied science, essential for the electronics, materials and energy future, it is also a field of frontier research with a window on new forms of collective behavior in matter, not just in the cryostat, but out in the cosmos at large.” Coleman is currently involved in research into heavy fermion superconductivity and quantum criticality, and is completing a book on many-body physics.