Staying focused

Irina Novikova

Viewpoint

Staying focused

Department of Physics, The College of William & Mary, Williamsburg, VA 23187-8795, USA

January 26, 2009• Physics 2, 7

The blurring effects of diffraction pose an obstacle to transmitting an image with all-optical technology. A method to reduce diffraction that takes advantage of the thermal motion of atoms could prove a way to keep images sharp.

Figure caption — **Figure 1:** (a) The three-level interaction scheme necessary for electromagnetically induced transparency (EIT) and the slowing of light. Without EIT both the control and signal optical fields drive an atom into the excited state that is followed by the spontaneous decay to the two ground states. Since the control field is much stronger, most atoms end up at the state $| c 〉$ , causing strong absorption for the signal field. Under EIT conditions (when $ω_{s} - ω_{c}$ is equal to the energy difference between states $| b 〉$ and $| c 〉$ ), however, the atoms are pumped into a quantum superposition of the states $| b 〉$ and $| c 〉$ (the dark state). Even though most of the atomic population is still in the state $| c 〉$ , the atoms do not interact with the signal field, resulting in a transparency window. (b) Schematic of diffractionless signal field propagation. By choosing the proper frequency difference between the control and signal frequencies, the diverging signal field couples preferentially to the atoms moving towards the propagation axis, which “drags” the signal light back.

In the modern world, information is almost a new currency, and everyone is trying to figure out how to transmit and process it faster, more efficiently and without losing one bit. Even though the success of fiber optics has made optical data transmission a reality, information is still largely processed electronically. The lure of all-optical data handling is that it promises to be more compact and efficient than electronics technology. In the last decade or so physicists and engineers have proposed and demonstrated a wide range of effects that may become stepping stones for all-optical networks, such as the controllable delay or advance of light pulses (“slow” or “fast” light) [1,2], the storage of optical pulses in atoms that preserve their quantum state (“stored” light) [3], ultralow threshold optical switches and other nonlinear devices [4].

Since “a picture says a thousand words”, there is also a lot of interest in the all-optical transmission and processing of images [5,6]. But although a lot of information can be compressed into the fine details of an image, diffraction will inevitably cause some distortions in an image as it propagates through free space toward a detector. In Physical Review Letters, Ofer Firstenberg and his colleagues from the Technion-Israel Institute of Technology and the Weizmann Institute of Science propose a new, exciting way to eliminate diffraction in the transmission of arbitrary images [7]. Unlike many previous experiments, they rely on moving atoms to correct the behavior of light, turning atomic diffusion—a traditional enemy of slow and stored light experiments [6]—into an unexpected ally.

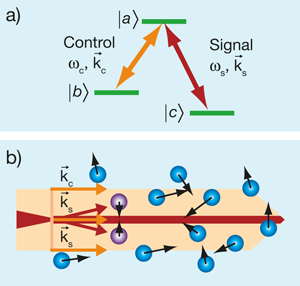
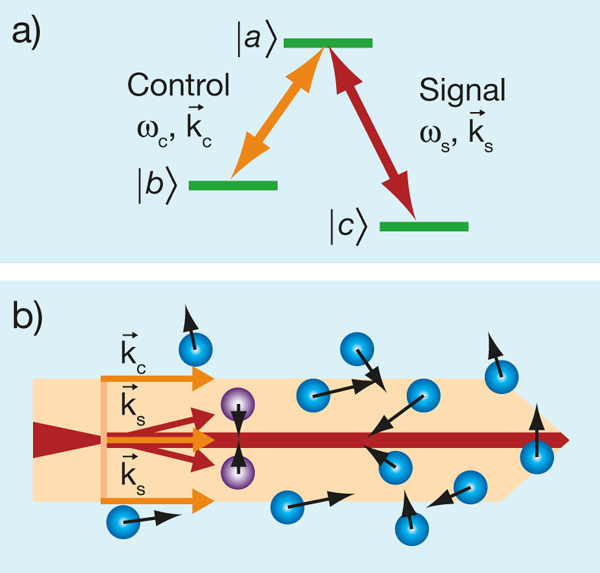
The search for efficient ways to control the propagation of light has been carried out by hundreds of research groups across the globe. One of the first methods developed for all-optical control of light pulse propagation is electromagnetically induced transparency (EIT) [3]. The essence of EIT is illustrated in Fig. 1(a): an atom interacts with both a strong control laser field and a weak signal laser field, with frequencies $ω_{c}$ and $ω_{s}$ , respectively, which optically pump the atom into a particular quantum superposition of two long-lived ground states ( $| b 〉$ and $| c 〉$ ) that is decoupled from the excited state $| a 〉$ . This quantum state is often called a “dark state”—atoms in this state cannot be promoted to the excited state $| a 〉$ , and do not fluoresce, leaving the atomic sample looking dark. EIT is a narrow-band coherent effect: the transparency occurs only in the vicinity of a two-photon resonance, when the frequency difference between the two laser fields, $ω_{s} - ω_{c}$ , matches the frequency splitting between the two atomic ground states $| b 〉$ and $| c 〉$ . Simultaneously, this narrow peak in transmission corresponds to a steep variation in the refractive index $n (ω)$ (and therefore the group velocity for the signal pulse) as a function of signal field frequency [1,3]. This is why the signal field “slows down” in an EIT medium. Both the width of the EIT resonance and the value of the dispersion ( $d n / d ω$ ) are proportional to the intensity of the control field, which (at least theoretically) means that EIT can be used to make a lossless and completely controllable optical delay element. By now, controlled pulse propagation based on EIT and its modification have been demonstrated in many systems, including hot and cold atomic and molecular gasses, solid-state materials, and nanostructures.

Of course, the applications of EIT are not limited by slow light. In fact, many research groups are exploring the possibility of guiding light inside an atomic sample by taking advantage of the high nonlinearity of EIT [8]. These experiments usually use the same basic guiding principle as a regular optical fiber, in which light is confined transversely inside a narrow core. The core is made out of a transparent material with a refractive index higher than the material that surrounds it so that light undergoes continual total internal reflection as it travels down the fiber. Similarly, in an EIT atomic medium, specially designed spatial patterns in the control field can create an inhomogeneous refractive index in the regions where the signal field propagates. As in the case of a regular fiber, only certain spatial modes of the signal field can be guided. Atomic diffusion is, however, a big problem, since moving atoms drift between regions of different control field intensity and blur the boundary between regions with a different index of refraction.

The diffraction-reducing approach proposed by Firstenberg et al. is fundamentally different: instead of creating a stationary waveguide, their method relies on moving atoms to “push” the diverging light back to its straight track. The Doppler effect is very important for moving atoms, and any deviations from collinear propagation of the control and signal fields lead to an effective two-photon detuning, $Δ k \cdot$ $υ$ , where $Δ k = k_{s} - k_{c}$ is the difference between the wave vectors of the two fields, and $υ$ is the velocity of the atom. Figure 1(b) illustrates this idea: if the control field is collimated (i.e., moving in parallel lines) and the signal field is diverging, it is possible to adjust the two-photon detuning to make the signal field couple more strongly with the atoms moving towards the center of the laser beams [the “purple” atoms in Fig. 1(b)]. As a result, the slowly propagating signal pulse is dragged back to the central region by moving atoms, preserving the spatial profile of the signal field. Exact calculations show that by adjusting the relative frequency of two fields by one EIT resonance width from the exact EIT conditions, the motional-induced dispersion can completely compensate the spreading of the beam due to both diffraction and atomic diffusion. In particular, the numerical simulations demonstrate the possibility to propagate a signal field in the slow light regime without losing its rather complex spatial distribution [Fig. 2]. The most exciting part is that the cancellation of diffraction happens automatically for any signal image, which makes it uniquely different from previous work. Also, more generally, this method can be though of as a new type of optical trapping—trapping of light by rapidly moving atoms.

It remains to be seen if this proposal will be realized and used in any practical applications. The main problem for such experiments may become a residual absorption that accompanies the cancellation of diffraction at the required two-photon detuning. It should be possible to restore the signal level using additional gain processes, although this can limit the application of such motional-induced light guiding for quantum information applications. However, there are still plenty of applications in optical data processing and image analysis that could potentially benefit from this method.

References

R. W. Boyd and D. J. Gauthier, in Progress in Optics, edited by E. Wolf (Elsevier, Amsterdam, 2002), Vol 43, p. 497[Amazon][WorldCat]
R. W. Boyd, D. J. Gauthier, and A. L. Gaeta, Opt. Photonics News 17, 18 (2006)
M. D. Lukin, Rev. Mod. Phys. 75, 457 (2003)
Min Xiao, Hai Wang, and David Goorskey, Opt. Photonics News 13, 44 (2002)
P. K. Vudyasetu, R. M. Camacho, and J. C. Howell, Phys. Rev. Lett. 100, 123903 (2008)
M. Shuker, O. Firstenberg, R. Pugatch, A. Ron, and N. Davidson, Phys. Rev Lett. 100, 223601 (2008)
O. Firstenberg, M. Shuker, N. Davidson, and A. Ron, Phys. Rev. Lett. 102, 043601 (2009)
See, for example, Richard R. Moseley, Sara Shepherd, David J. Fulton, Bruce D. Sinclair, and Malcolm H. Dunn, Phys. Rev. Lett. 74, 670 (1995); A. G. Truscott, M. E. Friese, N. R. Heckenberg, and H. Rubinsztein-Dunlop, 82, 1438 (1999)

About the Author

Irina Novikova earned her undergraduate Diploma in physics from the Moscow State Engineering-Physics Institute in 1998. She completed her Ph.D. in 2003 in experimental Atomic and Molecular Optics at Texas A&M University under the supervision of Prof. George R. Welch. After spending three years as a postdoctoral fellow at the Harvard-Smithsonian Center for Astrophysics, she joined the physics faculty at the College of William & Mary. Irina’s research is focused on the investigation of coherent light–atom interactions and their applications for quantum optics, precision metrology, and telecommunications.