Exciting rogue waves
Rogue waves [1]—extreme ocean waves with heights up to thirty meters—have been common elements in stories from people working at sea, as well as in popular fiction. It is not hard to imagine why: being on a small boat in a stormy sea swell and suddenly encountering a wave maybe three times as high as the surrounding waves is a terrifying experience (Fig. 1). However, up to a few decades ago, oceanographers mainly investigated the surface of the sea using linear models and these models could not account for the numerous occurrences of rogue waves reported by seafarers and ocean workers. In fact, it was not until 1995 that the first proper measurement of a rogue wave was made. Yet the conditions that cause such waves to grow enormously in size are not well understood. Recent results reported in Physical Review A by Nail Akhmediev and Adrian Ankiewicz of the Australian National University and Jose Soto-Crespo of Instituto de Óptica, Madrid, Spain [2], answer some of these questions and could also increase our understanding of how to produce high-intensity electromagnetic pulses in optical media.
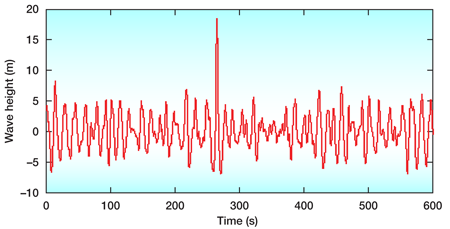
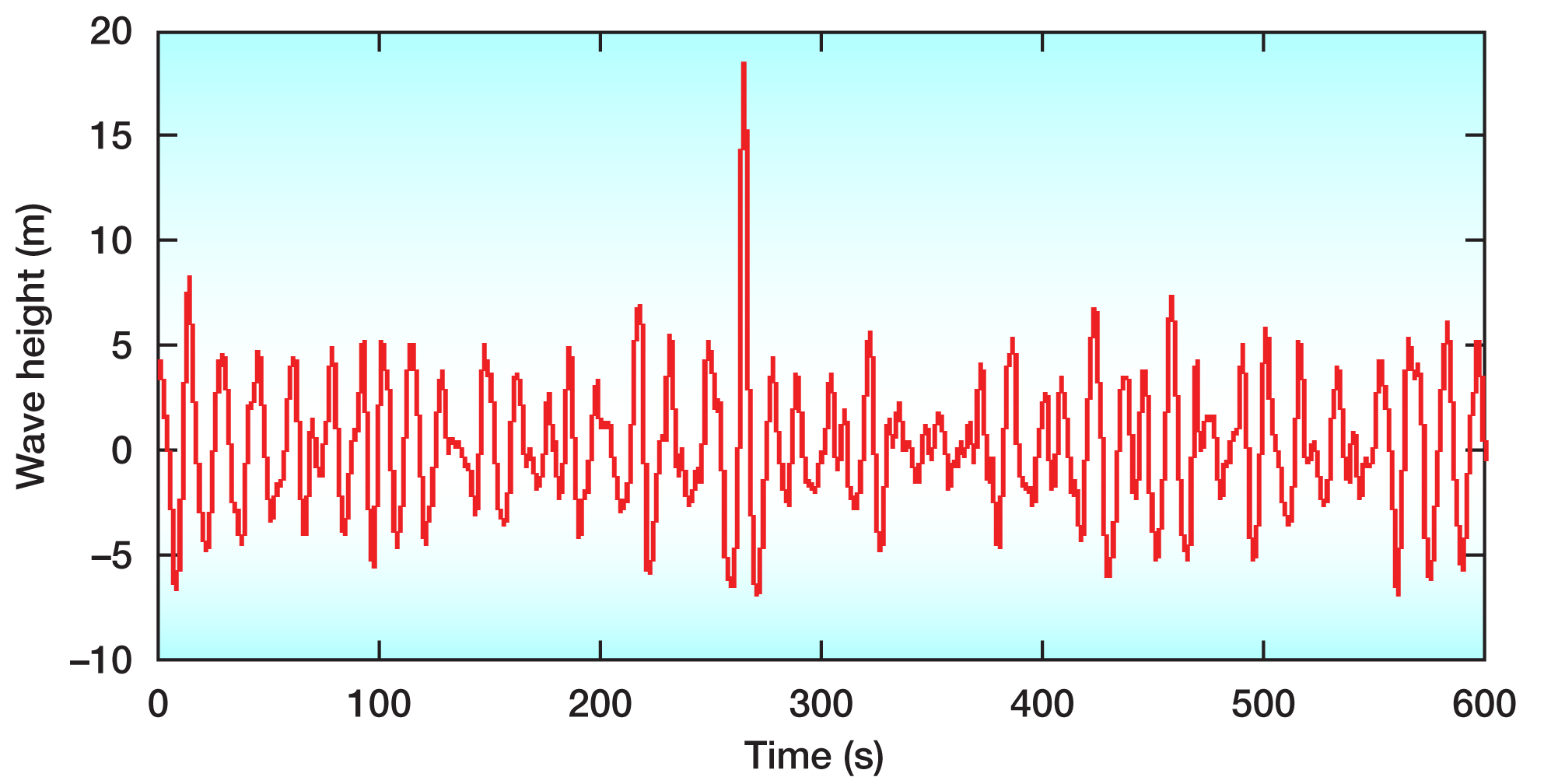
As far as ocean waves are concerned, we have good data about occurrences of these freaks of nature. On 1 January 1995, the oil platform Draupner in the North Sea was hit by a steep rogue wave with a height of eighteen meters, while the surrounding sea swell contained waves below ten meters in height (Fig. 2). Taking into account the surrounding wave troughs, the Draupner wave measured a staggering twenty-six meters in size from bottom to top [3]. Since then, a large number of measurements have been made, and the satellite based project MaxWave [4] has conclusively determined that such rogue waves are much more common than what can be expected from linear wave models (e.g., Ref. [5]).
So what is the mechanism behind the occurrence of such extreme waves? What we know now suggests that rogue waves form due to the nonlinear interactions between surface waves [6,7]. The remaining question is how to model these nonlinear properties. While ocean dynamics in general can be determined from the Navier-Stokes equations, these are extremely complex to solve, but simplified nonlinear wave models based on these equations can be derived. In particular, nonlinear water surface waves can, under suitable conditions, be modeled by a nonlinear Schrödinger equation, giving the evolution of the wave in terms of its amplitude and phase. In this case, a confining potential is created by the wave itself, for which the potential depth depends on the height of the wave. This confinement, or self-interaction, competes with the regular dispersion of the wave, a competition that makes formation of stable waves called solitons possible. This gives rise to some of the remarkable properties of such nonlinear ocean waves. Although the nonlinear Schrödinger model is the result of a series of approximations, it captures the essential features of rogue wave formation.
Interestingly enough, the nonlinear Schrödinger equation not only gives a suitable description of rogue water waves, it is also the standard equation for treating propagation of light pulses in nonlinear optical fibers [8], as well as for a multitude of other phenomena, ranging from the dynamics of Bose-Einstein condensates to relativistic laser-plasma interactions [9]. In optical fibers, the material properties are tuned to respond to the intensity of the incoming light to create a self-focusing effect, balancing the dispersive spreading of the light wave. This gives rise to optical solitons, light pulses that can cross large distances in a fiber without information loss [10]. Since these light waves are described by the same type of equation as rogue waves, the use of optical systems as analogues of nonlinear water waves has been suggested. Indeed, Solli et al. [11] used this principle to investigate the occurrence of rogue waves in optical systems. They found that initially smooth pulses developed rogue waves due to optical noise, in line with what is to be expected from real rogue waves formed in a random sea swell.
More accurate models, extensions of the single nonlinear Schrödinger equation, have been developed in the literature, such as the Dysthe model (taking into account that the waves may have a broad spectrum) [12], or interacting nonlinear wave models, for which one has a set of coupled nonlinear Schrödinger equations [7,13]. Such models lend further support to the accuracy of these simple models concerning the evolution of ocean waves into giant waves. In particular, the coupling of two different wave systems shows behavior very reminiscent of a real stormy sea. Thus these simplistic nonlinear descriptions provide important insights into rogue wave formation.
However, while the above models show how a given wave system evolves, they do not tell us the suitable initial conditions for such waves to grow from. For predictive purposes, such knowledge is of utmost importance, and could help improve our understanding of rogue waves. Moreover, in reality, the state of the sea in which rogue waves form is often highly erratic and turbulent [6]. So how does one go about finding predictive information from these rather simple models of ocean waves? In particular, what kind of initial conditions seed rogue waves? Finding the statistics and scaling properties of rogue wave formation based on a system of coupled nonlinear waves and a given set of random initial wave distribution is one way of obtaining predictive information of ocean wave evolution [14].
Using random data as initial conditions for wave evolution is natural from the perspective of ocean waves, and the mechanisms behind the formation of rogue waves from such initial data are reasonably well understood. However, random initial data make it difficult to control the special wave features that give rise to rogue waves. Thus Akhmediev et al. approach the issue of initial conditions along a quite different route. Rather than using random initial conditions, they look for well-determined initial conditions that immediately lead to the formation of a rogue wave. In particular, these authors have chosen to investigate the dynamics of so-called “breathers” [15,16]. Such particular solutions to the nonlinear Schrödinger equation exhibit localization in space or time while showing a large amplitude periodic oscillation in time or space, respectively. Thus these waves can, just like ocean rogue waves, appear from nowhere and disappear without a trace. Akhmediev et al. [2] studied collisions of two or three breathers and found that such wave solutions and interactions can indeed help us in modeling rogue wave phenomena. In particular, the analysis in Ref. [2] indicates why we need special conditions for the creation of rogue waves. There are two main caveats for the production of large amplitude waves in these collisions: it requires both timing and precision, as the time-varying crests should overlap at exactly the right spot to produce maximum amplitude. Determining the right initial conditions for this optimization to occur, therefore, is crucial, and this is what Akhmediev et al. has analyzed. The results in Ref. [2] indicate that once the right initial conditions have been given, rogue waves will almost certainly appear.
Understanding the features of the initial data that form the basis for the formation of extreme waves has applications to more than just the field of oceanography. For example, in optical systems, it would be valuable to be able to predict the initial conditions of the light pulse so as to produce extreme intensity pulses at well-determined positions and time steps. While there are technical difficulties in such an approach, such as obtaining the right material properties for the nonlinear optical medium, it is certainly a very interesting approach to high-intensity light pulse formation. Furthermore, one can also imagine applications to other fields of studies, e.g., laser-plasma interactions, where the right initial data perhaps could aid the acceleration of particles [9]. The future may hold several surprises regarding the use of the results presented by Akhmediev et al. to probe these giant waves.
References
- P. Müller, Ch. Garrett, and A. Osborne, Oceanography 18, No. 3, September (2005); http://www.tos.org/oceanography/issues/issue_archive/18_3.html
- N. Akhmediev, J. M. Soto-Crespo, and A. Ankiewicz, Phys. Rev. A 80, 043818 (2009)
- C. Kharif and E. Pelinovsky, Eur. J. Mech. B 22, 603 (2003)
- http://www.esa.int/esaCP/SEMOKQL26WD_index_0.html
- P. C. Liu and U. F. Pinho, Ann. Geophys. 22, 1839 (2004)
- M. Onorato, A. R. Osborne, M. Serio, and S. Bertone, Phys. Rev. Lett. 86, 5831 (2001)
- P. K. Shukla, I. Kourakis, B. Eliasson, M. Marklund, and L. Stenflo, Phys. Rev. Lett. 97, 094501 (2006)
- G. P. Agrawal, Nonlinear Fiber Optics (Academic Press, San Diego, 2001)[Amazon][WorldCat]
- Special Issue, edited by P. K. Shukla, Phys. Scripta T113 (2004)
- A. Hasegawa and F. Tappert, Appl. Phys. Lett. 23, 142 (1973)
- D. R. Solli, C. Ropers, P. Koonath, and B. Jalali, Nature 450, 1054 (2007)
- K. B. Dysthe, Proc. R. Soc. London A 369, 105 (1979)
- M. Onorato, A. R. Osborne, and M. Serio, Phys. Rev. Lett. 96, 014503 (2006)
- A. Grönlund, B. Eliasson, and M. Marklund, Europhys. Lett. 86, 24001 (2009)
- K. B. Dysthe and K. Trulsen, Phys. Scripta T82, 48 (1999)
- A. I. Dyachenko and V. E. Zakharov, JETP Lett. 88, 307 (2008)
- http://www.math.uio.no/~karstent/waves/index_en.html