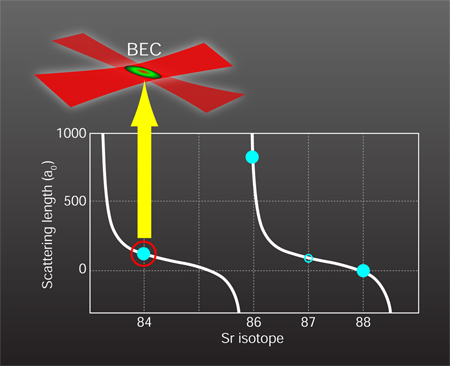
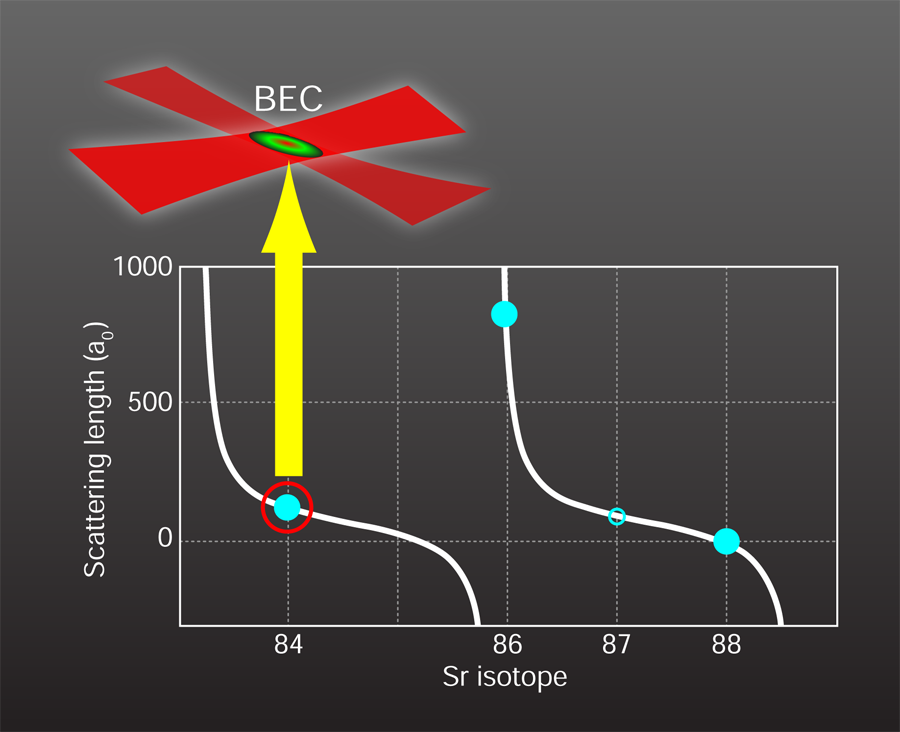
—just right for forming a Bose-Einstein condensate

Tanya Zelevinsky

Viewpoint

$^{84} Sr$ —just right for forming a Bose-Einstein condensate

Tanya Zelevinsky

Department of Physics, Columbia University, 538 West 120th Street, New York, NY 10027-5255, USA

November 9, 2009• Physics 2, 94

Two separate teams have achieved the long sought after Bose-Einstein condensation of strontium.

Figure caption — **Figure 1:** At ultracold temperatures, the interactions between atoms depend mostly on the scattering length. The natural abundance of $^{84} Sr$ is only $0.6 %$ , but the mass scaling of the well-known scattering length of $^{88} Sr$ leads to the prediction that the scattering length of $^{84} Sr$ is perfectly suited for evaporative cooling [9]. The inset shows that for the $^{84} Sr$ isotope, the important step of evaporative cooling—where the hottest atoms in precooled atom samples boil out of the dipole trap formed by two crossed laser beams—is effective at creating a large Bose-Einstein condensate.

At extremely low temperatures, the fact that atoms and molecules obey either Bose or Fermi statistics starts to dominate their behavior. When the density is sufficiently high, and the temperature is below a critical value, a thermal gas of identical Bose atoms precipitates into a collective state known as a Bose-Einstein condensate (BEC). In this quantum degenerate gas, all atoms are trapped in the same internal state, and possess zero quanta of kinetic energy.

The first BECs were created in 1995 from gases of alkali metal atoms, which are hydrogenlike atoms that have one electron in their outer shell [1]. As techniques have advanced, atomic physicists have been able to make quantum degenerate gases from a small number of atomic species with two valence electrons, such as ytterbium ( $Yb$ ) [2] and calcium ( $Ca$ ) [3]. In two papers [4] appearing in Physical Review Letters, Simon Stellmer and colleagues at the Universität Innsbruck in Austria and Natali Martinez de Escobar and colleagues at Rice University in Texas, US, report the first sightings of what has been, until now, an elusive BEC of another atom with two valence electrons: strontium ( $Sr$ ). Because $Sr$ offers a choice of particularly well-defined electronic transition frequencies, it is a key player in the blossoming fields of precision frequency metrology [5], quantum information [6], and ultracold chemistry [7]. The successful cooling of strontium into the quantum degenerate regime opens exciting possibilities in these young and largely experimental fields, giving researchers a valuable tool for controlling and engineering the interactions between the atoms.

Although ultracold $Sr$ has had a prominent role in experimental atomic physics and quantum optics in recent years, experimentalists have struggled to form a quantum condensate of this alkaline-earth atom. The final step in forming a condensate of alkali atoms like sodium and rubidium is evaporative cooling, where the depth of a trapping potential is slowly lowered so as to let out the hottest atoms [1]. The trapping potential is normally provided by a magnetic field. However, this is not very effective for trapping $Sr$ , which has no electronic magnetic moment in its ground state (the two electron spins in strontium’s valence shell line up to cancel the net electronic angular momentum) and a very small nuclear spin. In 2001, this problem was solved by showing that tightly focused laser beams could not only trap atoms but also evaporatively cool them to a BEC [8].

The remaining difficulty with obtaining strontium condensates is the magnitude of the cross section for two $Sr$ atoms scattering from one another, which is characterized by the quantum mechanical scattering length. The most abundant isotope of strontium obeying Bose statistics is $^{88} Sr$ ( $83 %$ ), followed by $^{86} Sr$ ( $10 %$ ). Unfortunately, the scattering length of $^{88} Sr$ is too small for efficient evaporation [9] since the atoms do not reach thermal equilibrium quickly, while the scattering length of $^{86} Sr$ is so large (see Fig. 1) that there is a high chance of lossy three-body interactions. The scattering length depends on the proximity of a bound state when two atoms approach each other. Since the probability for forming bound states is partly determined by the atoms’ masses, different isotopes of the same atom can have greatly varying scattering lengths. An attractive feature of the “two-electron” atoms, like $Sr$ , $Ca$ , and $Yb$ , is the availability of many stable isotopes, both bosons and fermions. Thus one can effectively tune interatomic interactions by choosing the most suitable isotope. Luckily, the boson $^{84} Sr$ ( $0.6 %$ abundance) has a scattering length of approximately one hundred Bohr radii. This not-too-small, not-too-large value is perfect for attempting to reach the high-phase-space densities needed for BEC.

To condense the strontium atoms, the two groups used similar methods that rely on classic BEC preparation techniques while utilizing the special properties of $Sr$ [4]. The most prominent feature of $Sr$ is that its two valence electrons can form spin singlet (electron spins antiparallel) or spin triplet (electron spins parallel) states. The ground state is a singlet, and transitions to the triplet states are nearly forbidden, resulting in long metastable lifetimes and narrow linewidths. To offset the low natural abundance of $^{84} Sr$ , the researchers continuously accumulate laser-cooled atoms in the metastable triplet state (lifetime of nine minutes), which carries a net spin, in a magnetic trap over several tens of seconds. This accumulation is a fortunate consequence of standard magneto-optical trapping of $Sr$ . The next laser-cooling step reduces the atoms’ temperature by about three orders of magnitude, to a microkelvin. To achieve these low temperatures with laser cooling alone, the researchers rely on another forbidden singlet-triplet transition (that has a lifetime of 22 microseconds) with an ultralow heating rate of the atoms by the laser. The final step to Bose-Einstein condensation is holding the atom cloud in a pair of crossed laser beams, and gradually reducing the laser’s intensity to allow the hottest atoms to boil off (inset, Fig. 1). When the temperature reaches the critical value (around $400 nK$ for both experiments), the phase-space density exceeds one, the atoms begin collapsing into the same quantum state, and a BEC emerges. The expansion of the condensed atom fraction after the gas is released from the trap is driven by the effective interaction between the atoms rather than the thermal energy. After another 1–2 seconds of evaporation, both groups detect pure condensates with atom numbers exceeding 100,000.

The new $Sr$ condensates appear somewhat more robust than those made from $Yb$ and $Ca$ , putting them in a prime position for use in a broad range of future experiments. With a successful recipe for making a condensate of $^{84} Sr$ in hand, it may be possible to form quantum degenerate gases of other $Sr$ isotopes. Physicists often use a technique called sympathetic cooling [10] to achieve quantum degeneracy of fermions that cannot cool themselves because of the Pauli exclusion principle. Similarly, this method can help overcome the tiny scattering length of $^{88} Sr$ . Since the interatomic interactions in a BEC of $^{88} Sr$ would be unusually small, a $^{88} Sr$ -BEC atom interferometer would not suffer from collisional effects. Thus it could be an excellent tool for precision sensors such as those detecting very small forces [11]. While other BECs can be made nearly noninteracting by magnetically tuning the atomic scattering length via “Feshbach resonances,” applying the necessary large magnetic fields to sensitive experiments is not always the optimal path.

When a BEC is held in an optical lattice—a light interference pattern analogous to a solid state crystal lattice—it can make a transition from a superfluid to a Mott insulating phase when the lattice potential is sufficiently deep [12]. In the Mott insulating phase, single atoms are confined to individual lattice sites and thus completely avoid collisions, even at the high densities. Strontium atoms in this state might find applications as qubits for quantum information storage and manipulation [6], as well as for time and frequency metrology, where collisional effects are currently among the limits to the best frequency standards based on fermionic $^{87} Sr$ [13].

Strontium BEC is exciting for many other directions in ultracold atom physics. For example, an optical technique called photoassociation can force the atoms to bind into molecules [14]. By starting with a condensed sample, this same technique could produce an ultracold, dense molecular gas near quantum degeneracy. Ultracold strontium diatomic molecules are a promising system for a new generation of molecular frequency standards that can independently confirm the stability of fundamental constants of nature [15]. Furthermore, molecules in which $Sr$ is bound to another atom can form new interesting states of matter with both electric and magnetic dipole moments. This can lend itself to engineering the lattice spin models of condensed matter physics [16].

The achievement of large, robust Bose-Einstein condensates of $^{84} Sr$ is an important step toward answering many fundamental questions. How do long-range interactions between molecules manifest themselves at ultralow temperatures? Are the fundamental constants of nature as constant as they appear? Can researchers make a quantum leap in information storage and retrieval techniques? The combination of the prominent role of $Sr$ in precision measurements with the achievement of macroscopic coherence and large phase-space density will bring many exciting advances.

References

M. Anderson et al., Science 269, 198 (1995); C. Bradley et al., Phys. Rev. Lett. 75, 1687 (1995); K. Davis et al., 75, 3969 (1995)
Y. Takasu et al., Phys. Rev. Lett. 91, 040404 (2003); T. Fukuhara et al., Phys. Rev. A 76, 051604 (2007); 79, 021601 (2009)
S. Kraft et al., Phys. Rev. Lett. 103, 130401 (2009)
S. Stellmer, M. K. Tey, B. Huang, R. Grimm, and F. Schreck, Phys. Rev. Lett. 103, 200401 (2009); Y. N. M. de Escobar, P. G. Mickelson, M. Yan, B. J. DeSalvo, S. B. Nagel, and T. C. Killian, 103, 200402 (2009)
S. Blatt et al., Phys. Rev. Lett. 100, 140801 (2008)
D. Hayes et al., Phys. Rev. Lett. 98, 070501 (2007); I. Reichenbach and I. Deutsch, 99, 123001 (2007); A. Daley et al., 101, 170504 (2008); A. Gorshkov et al., 102, 110503 (2009)
T. Zelevinsky et al., ChemPhysChem 9, 375 (2008); C. Koch, Phys. Rev. A 78, 063411 (2008); R. Ciurylo et al., 70, 062710 (2004)
M. Barrett et al., Phys. Rev. Lett. 87, 010404 (2001)
Y. Martinez de Escobar et al., Phys. Rev. A 78, 062708 (2008)
D. Larson et al., Phys. Rev. Lett. 57, 70 (1986); R. deCarvalho et al., Eur. Phys. J. D 7, 289 (1999); C. Myatt et al., Phys. Rev. Lett. 78, 586 (1997)
M. Fattori et al., Phys. Rev. Lett. 100, 080405 (2008); M. Gustavsson et al., 100, 080404 (2008)
D. Jaksch et al., Phys. Rev. Lett. 81, 3108 (1998); M. Greiner et al., Nature 415, 39 (2002)
G. Campbell et al., Science 324, 360 (2009)
K. Jones et al., Rev. Mod. Phys. 78, 483 (2006)
T. Zelevinsky et al., Phys. Rev. Lett. 100, 140801 (2008)
A. Micheli et al., Nature Phys. 2, 341 (2006)

About the Author

Tanya Zelevinsky received her Ph.D. at Harvard University in 2004, working on precision measurements of helium fine structure. She was a Postdoctoral Associate at JILA and the University of Colorado until 2007, where her team developed the optical lattice clock based on fermionic strontium. She became an Assistant Professor of Physics at Columbia University in 2008.